시리즈 | Linear Algebra - 0.선형대수학의 슬픔

인생이 슬프다. 선형대수학이 이유다.

요 근래 뭔가를 깊게 배우려고 하면 항상 선형대수학을 마주친다.
인공지능을 공부하려고 책을 열어보면 2장부터 Eigen Decomposition, Positive semi-definite, Singular Vector Decomposition, Moore Penrose pseudo inverse 등등 무서운 게 많다. 슬프다. 심지어 증명도 없이 기술만 돼 있는 것 때문에 더 슬프다.

그러다가 물리를 열어보면 갑자기 눈 앞에 텐서가 있다. 관성 텐서, Maxwell Stress Tensor 등등 무서운 게 갑자기 나타난다. 표기의 타당성 등은 선형대수학에서 배우란다. 슬프다.

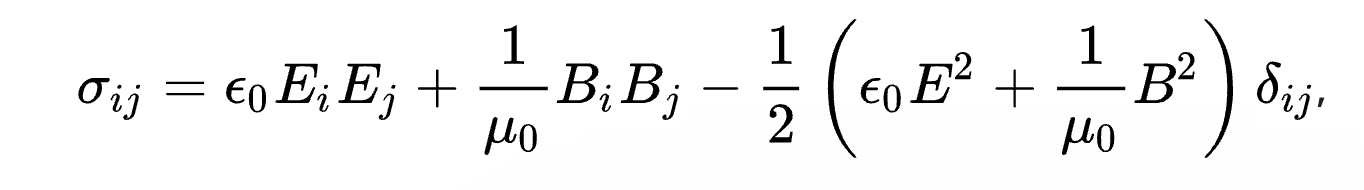
다시 수학으로 돌아와서 미분방정식 발표를 준비하다 보니까 또 공간과 차원이 눈 앞에 나타난다. 진지하게 슬프다.

이런 이상한 주제들에 지쳐 생명과학으로 도망쳤는데, 거기서도 이상한 행렬이 있었다. 안 믿기겠지만 계통수에 대한 발표​​이다. 생물에서도 선형대수학이라니 말이 안된다.

수학 물리 생물에 모두 지쳐 지구과학으로 도망갔으나 역시 지구과학에도 선형대수학이 있었다. 슬프다.

지금까지는 매번 필요한 선형대수학 지식을 그 때 그 때 찾아가면서 버텨왔다. 하지만 이런 일이 너무 많아지기도 하고, 많은 사람이 이렇게 슬퍼할 것 같아서 선형대수학 지식을 예쁘게 정리해보고자 한다.

사실 다들 선형대수학 강의를 생각하면 그냥 벡터랑 행렬 얘기 아닌가? 생각할 것이다. 근데 여기 저기서 주워 듣다 보면, 선형대수학(이하 선대)을 다루다 보면 항상 빠지지 않고 공간이란 단어가 따라오는 것을 알 수 있다. 앞선 예시에서도 중간중간 해 공간, 차원이란 단어가 나오는 것을 볼 수 있다.

조심스럽게 말해보자면 사실 선형대수학은 공간에 대한 학문인 것 같다. 기초적인 공간을 기술하는 방법으로 벡터를, 공간 간 대응을 기술하는 방법으로 행렬을 이용한 것으로 보인다.

시리즈의 구성

그런데 공간이 무엇인가. 뭔가 어디선가 들어서 쓰고는 있지만 공간, 차원 등등에 대한 엄밀한 정의를 배운적이 없다. 단순히 공간, 차원 등의 단어 뿐만 아니라 백터 등의 단어도 엄밀한 정의 없이 사용하는 듯 하다.
이런 문제를 해결하고자 선형대수학을 완전 기초부터 다뤄보고자 한다. 백터 공간, 선형사상, 행렬, 선형연립방정식, 행렬식, 대각화, 내적공간 등등에 대해 다뤄볼 듯 하다. 사실 필자도 선형대수학을 공부하고, 복습하면서 글을 작성하는 것이기에 시리즈의 구성이 달라질 수 있다.

시리즈를 읽을 때 주의할 점

사실 선형대수학을 다루는 글인 만큼, 논리 전개에 있어서 선형대수학과 관련된 사전 지식을 요구하지는 않는다. 하지만 이해를 돕기 위한 수단으로 행렬곱, 내적 등의 백터 연산을 예시로 제시할 수 있다. 이에 대해 잘 모른다면, 필자가 Cramer Rao Lower Bound에 대해 정리해놓은 글에서 행렬에 대해 간단히 정리해놓았으니 이를 읽고 오면 좋을 듯 하다!

글을 마무리하면서...

이 글과 시리즈를 쓰는 필자 역시 평범한 고등학생에 불과하므로, 내용 중 틀린 부분이 있을 수 있다. 뭔가 이상하다면 댓글로든 다른 수단으로든 편하게 지적해보자!
글은 Friedberg의 Linear Algebra(4ed)를 참고하며 쓰려고 하니, 더 알아보고 싶다면 해당 책을 참고해도 좋을 듯 하다.

또, 향후 이 시리즈의 글에 다소 수식과 현학적인 내용이 많을 것 같아 이번 글은 다소 뇌에 힘을 빼고 써보았다. 다음 글부터는 뇌에 힘을 주고 쓸 예정이니 이 부분은 걱정하지 않아도 좋다!