시리즈 | Quantum Chemistry - 1. 흑체 복사와 양자역학의 태동

지난 글에서 우리는 양자화학이 무엇인지, 그리고 양자화학의 토대인 양자화학이 왜 중요한지에 관해 알아보았다. 양자역학을 본격적으로 알아보기 전에, 양자역학이라는 이론이 새롭게 발생한 계기는 무엇인지 궁금하지 않는가? 그 해답은 바로 고전역학이 흑체 복사 현상을 잘 설명하지 못하는 "자외선 파탄"으로부터 촉발된 "플랑크의 에너지 양자화 가설"에 있다.

흑체 복사란?

자외선 파탄과 플랑크의 에너지 양자화 가설을 알아보기 이전에, 흑체가 무엇인지, 그리고 흑체 복사란 도대체 어떤 현상인지부터 알아보자.

흑체란 진동수, 입사각에 상관없이 모든 전자기파를 흡수하는 이상적인 물체이다. 이런 흑체는 단순히 에너지를 흡수하기만 하는 것이 아니라, 전자기 복사의 형태로 에너지를 방출하기도 한다. 이와 같이 흑체가 전자기 복사의 형태로 전자기파를 방출하는 현상을 흑체 복사라고 한다.

예를 들어서, 동글동글한 쇠구슬을 불로 달구는 상황을 생각해보자. 처음에는 쇠구슬이 가열되면서 붉게 변하고, 온도가 충분히 올라가 열평형에 도달하면 결국 하얗게 빛을 뿜어낸다. 이 상태가 바로 흑체랑 매우 비슷하다.

아래 영상을 보고 넘어가자. 아래 영상에는 인덕터를 활용하여 쇠 막대를 가열하고 있는데, 순식간이긴 하지만 빨개지다가 하얘지는 것을 볼 수 있다.

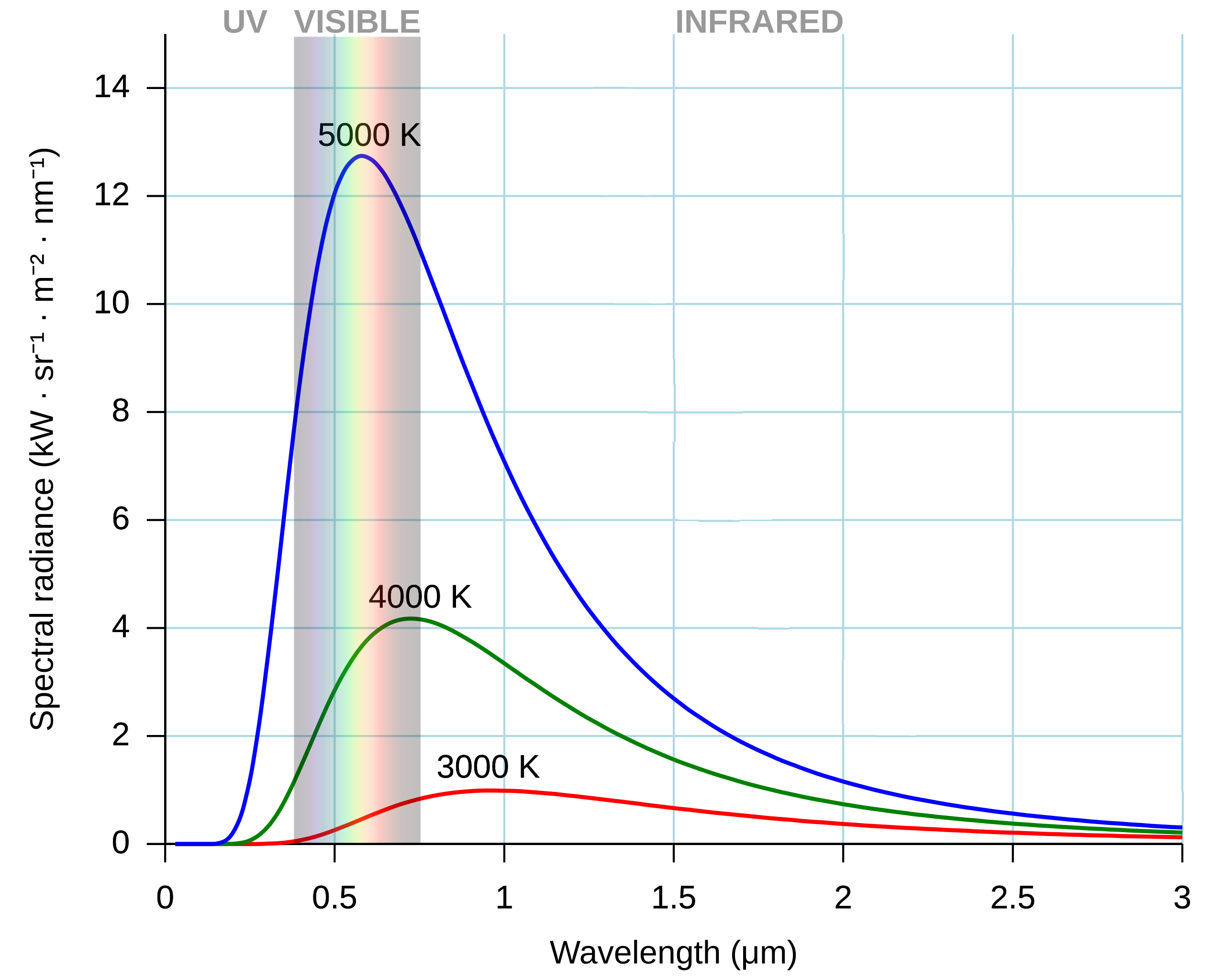
흑체가 전자기파 흡수와 방출을 반복하다 보면, 흡수 세기와 방출 세기가 같아져 내부 에너지 변화와 온도 변화가 없는 상태에 도달해 열평형을 이루게 된다. 열평형 상태의 흑체는 이상적 방출체의 특성을 띄며, 온도에 의존하여 전자기파를 복사한다. 특히, 흑체 복사 스펙트럼은 흑체의 종류와는 무관하게 오직 온도에만 의존한다.

흑체 복사 법칙

레일리 진스와 같은 과학자들은 흑체 복사 현상을 보고, 진동수별로 흑체가 방출하는 전자기파의 세기를 모델링하고자 하였다. 따라서, 과학자들은 흑체를 공동으로 이상화하고, 전자기파가 공동 내부에서 아래 그림과 같이 벽과 상호작용하며 열평형 상태에 도달한 뒤 방출된다고 보았다. 다시 말해서, 전자기파는 흑체 내에서 정상파를 이뤄 진동하며, 흑체의 벽을 이루는 진동자와 에너지를 교환한다고 가정하였다.

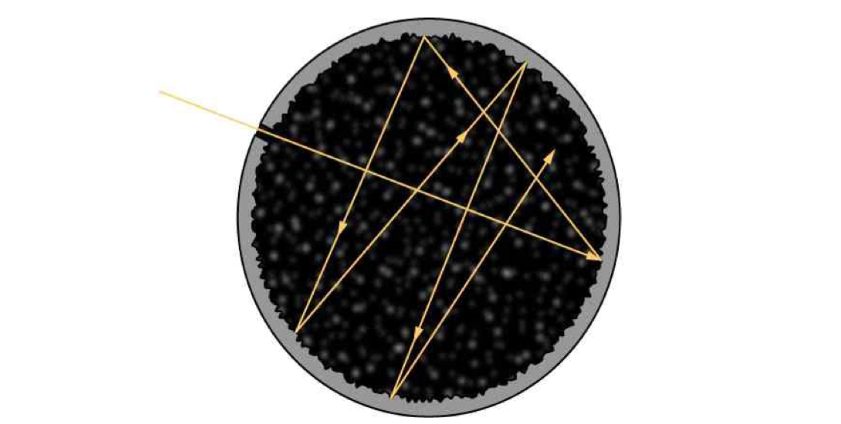
전자기파가 흑체 내에서 정상파를 이루고 진동자와 에너지를 교환하며 진동하고 있기 때문에, 진동수에 따라 흑체가 방출하는 에너지 밀도($dE$)는 정상파의 수 밀도($dN_{\rm{v}}$) 곱하기 진동자의 에너지($\braket{E}$)로 볼 수 있다.

그리고, 음함수의 미분을 할 때 옆에 $dy/dx$가 붙는 것과 비슷하게, 전체 에너지 밀도는 파장에 의존하기 때문에 에너지 밀도는 진동수의 미소 변화량($d\nu$)에 어떤 함수가 곱해진 형태로 나타낼 수 있다. 여기서 이 "어떠한 함수"를 에너지 상태 밀도라 하고, $\rho (\nu, T)$라 표기한다. 지금까지 한 얘기를 수식으로 적으면 다음과 같다.

$$ dE(\nu, T) = \rho (\nu, T)d\nu = \braket{E} dN_{\rm{v}}$$

이제부터 우리의 임무는, 정상파 수 밀도와 진동자의 에너지를 구하는 것이다! 각각 차근차근 구해서 흑체 복사 공식을 완성해나가 보자.

정상파 수 밀도 공식의 유도

먼저, 정상파 수 밀도를 유도해보자. 이 글에서는 각 변의 길이가 $L$인 정육면체 모양의 공동을 가진 흑체에 대해서 정상파 수 밀도를 유도해보자.

위에서 열평형 상태의 흑체 내 공동에서 전자기파는 정상파를 이룬다고 했으므로, 각 변의 길이는 반파장의 자연수배여야 한다. 다시 말해서, 정육면체의 각 변을 x축, y축, z축으로 잡고, 진행하는 파동의 파장을 각 축으로 정사영한 길이를 $\lambda _{x}$, $\lambda _{y}$, $\lambda _{z}$라고 하면 다음 식이 성립한다.

$$L = \frac{\lambda_{x}}{2} j_{x},\, L = \frac{\lambda_{y}}{2} j_{y},\, L = \frac{\lambda_{z}}{2} j_{z} \; (단, j_{x}, j_{y}, j_{z}는\;자연수)$$

L이 반파장의 몇 배인지 나타내는 수인 $j_{x}$, $j_{y}$, $j_{z}$에 관해 풀어주면 다음과 같다.

$$j_{x} = \frac{2L}{\lambda _{x}},\, j_{y} = \frac{2L}{\lambda _{y}},\, j_{z} = \frac{2L}{\lambda _{z}} $$

이제, $j_{x}$, $j_{y}$, $j_{z}$ 사이의 관계를 찾기 위해서, $\lambda_{x}$, $\lambda_{y}$, $\lambda_{z}$에 관한 식을 구해 보자. 위에서 $\lambda_{x}$, $\lambda_{y}$, $\lambda_{z}$는 진행하는 파동의 파장을 각 축으로 정사영한 길이라고 하였으므로, 파동의 방향이 x, y, z축과 이루는 각도를 각각 $\alpha$, $\beta$, $\gamma$로 둔다면 다음 그림과 같이 생각할 수 있다. (3D에 그리려니까 머리가 터질 것 같아서 xy평면에 에 찌부시켜서 그렸다.)

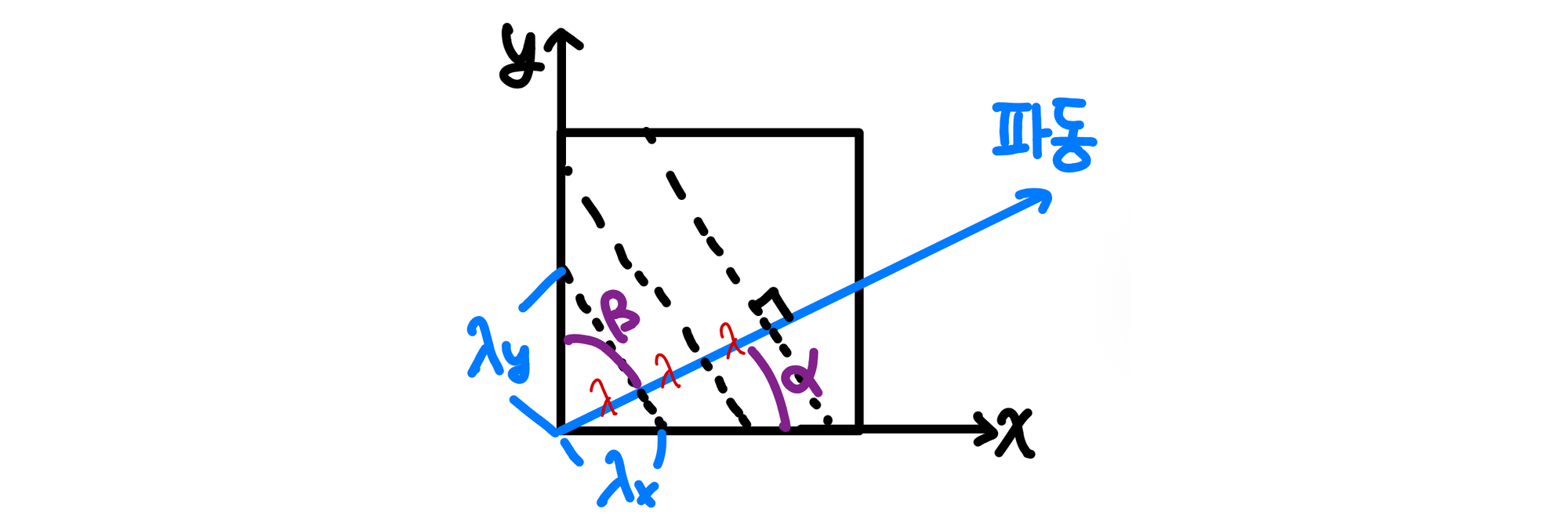
위 그림에 따라, 다음이 성립함을 알 수 있다. (z축은 위 그림에 없지만, 똑같이 생각해보자.)

$$\lambda = \lambda_{x} \rm{cos} \alpha = \lambda_{y} \rm{cos} \beta = \lambda_{z} \rm{cos} \gamma$$

이제 $\lambda_{x}$, $\lambda_{y}$, $\lambda_{z}$에 관한 식을 구했으니, $j_{x}$, $j_{y}$, $j_{z}$ 사이의 관계를 구해보자. $j_{x}$, $j_{y}$, $j_{z}$의 제곱의 합을 구하면...

$$j_{x} ^{2} + j_{y} ^{2} + j_{z} ^{2} = 4L^{2}(\frac{1}{\lambda_{x}^{2}} + \frac{1}{\lambda_{y}^{2}} + \frac{1}{\lambda_{z}^{2}}) \\ = \frac{4L^{2}}{\lambda^{2}} (\rm{cos}^{2} \alpha + \rm{cos}^{2} \beta + \rm{cos}^{2} \gamma)$$

여기서, 방향코사인의 제곱의 합은 1임을 활용하면, 다음과 같은 식을 도출할 수 있다.

$$j_{x} ^{2} + j_{y} ^{2} + j_{z} ^{2} = (\frac{2L}{\lambda})^{2}$$

다시, 정상파의 수 밀도로 돌아와보자. 정상파의 수 밀도를 구하기 위해서 우리는 정상파의 개수를 세야 한다. 정상파 상태는 $j_{x}$, $j_{y}$, $j_{z}$에 따라 하나씩 대응되므로, 정상파의 개수는 $(j_{x}, j_{y}, j_{z})$의 개수임을 알 수 있다.

지금 우리는 진동수의 미소 변화량에 대한 정상파 밀도를 구하고 있기 때문에, 특별히 $\nu$(진동수)가 변했을 때 j의 미소 변화량인 "dj"에 해당하는 정상파의 개수를 센다. 따라서, j에서 j+dj의 범위에 있는 순서쌍의 개수를 셀 거다. 정상파의 개수를 세기 위해 우리는 x, y, z 공간 대신에 "j 공간"에서 생각한다. j 공간에서 $j_{x} ^{2} + j_{y} ^{2} + j_{z} ^{2} = (\frac{2L}{\lambda})^{2}$ 식은 아래 그림과 같이 구 위의 점을 나타낸다.

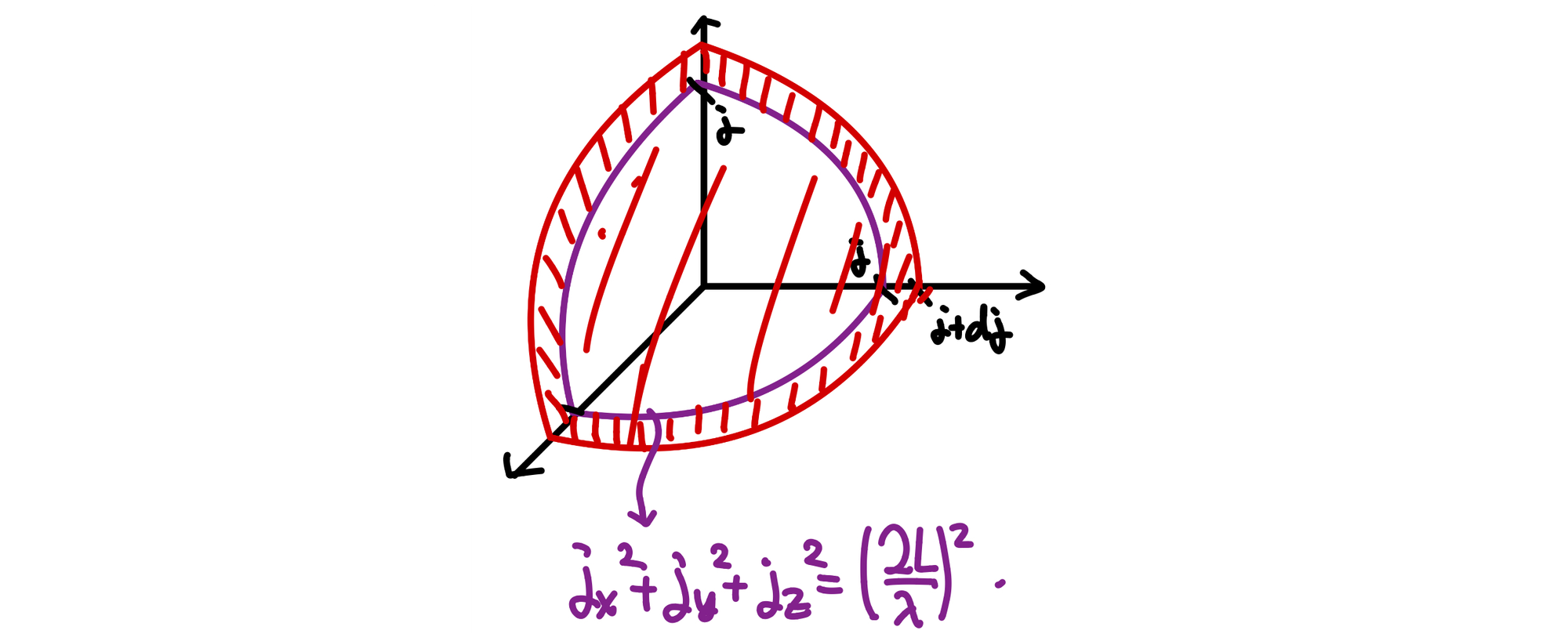
사실 $j_{x}$, $j_{y}$, $j_{z}$는 자연수이기 때문에, 원래는 점의 개수를 이산적으로 세어야 한다. 하지만, 빛의 파장에 비해 흑체의 크기는 매우 크기 때문에, $(j_{x}, j_{y}, j_{z})$ 쌍이 무수히 많고, 따라서 j 공간에서 $(j_{x}, j_{y}, j_{z})$는 연속하다고 근사한다.

따라서, $(j_{x}, j_{y}, j_{z})$ 쌍의 개수, 다시 말해서 정상파의 개수($g(\nu)d\nu$)는 구각 중 양수 부분의 부피를 말하고, 다음과 같이 쓸 수 있다. 여기서 빛에서는 전자기파가 왼쪽으로 회전하면서 진행하는 좌원편광과 오른쪽으로 회전하며 진행하는 우원편광 2가지 종류가 있으므로 맨 앞에 2를 곱한다.

$$g(\nu)d\nu = 2 \times \frac{1}{8} \times 4\pi j^{2} dj = \pi j^{2} dj$$

$j = \frac{2L}{\lambda} = \frac{2L}{c / \nu} = \frac{2L\nu}{c}$이므로, $dj = \frac{2L}{c} d\nu$가 성립한다. 또한, 정상파 밀도($dN_{v}$, $G(\nu)d\nu$)는 정상파의 개수를 공동의 총 부피로 나눈 값이므로, 정상파 밀도는 다음과 같다.

$$dN_{\rm{v}} = G(\nu)d\nu = \frac{1}{L^3} g(\nu)d\nu = \frac{1}{L^3} \pi {(\frac{2L \nu}{c}})^{2} \frac{2L}{c} d\nu = \frac{8\pi \nu ^{2}}{c^{3}} d\nu$$

다시 정리하면, 정상파 수 밀도 공식은 다음과 같다!!!

$$dN_{\rm{v}} = \frac{8\pi \nu ^{2}}{c^{3}} d\nu$$

Rayleigh-Jeans 복사 법칙과 자외선 파탄

Rayleigh-Jeans는 흑체 복사 법칙에 관해 연구하면서 이제 그렇게 어려운 정상파 밀도 공식 유도를 마치고 비교적 간단한 평균 에너지의 유도만 남았다고 신나하고 있었다. 얼른 고전 역학에 따라 평균 에너지를 계산했지만, 실제 실험 결과와 매우 다른 "자외선 파탄(Ultraviolet Catastrophe)"에 마주하게 되었다! (쌰갈!!!) 이 파트에서는 Rayleigh-Jeans가 평균 에너지를 계산한 방식을 알아보고, 자외선 파탄에 관해 알아보자.

지금까지 유도한 걸 중간 점검해보자.

$$ dE(\nu, T) = \rho (\nu, T)d\nu = \frac{8\pi \nu ^{2}}{c^{3}} \braket{E}d\nu$$

레일리 진스는 평균 에너지가 운동 에너지와 퍼텐셜 에너지의 합으로 표현되며 각 에너지는 연속된 값을 가지며, 모든 입자가 볼츠만 분포(입자가 특정 에너지 상태에 점유할 상태는 $e^{-\frac{ E_i }{kT}}$에 비례함, $P_i \propto e^{-\frac{ E_i }{kT}}$)를 따른다고 생각하였다. 따라서, 볼츠만 분포를 확률밀도함수라고 생각하고 에너지의 평균값을 다음과 같이 적분의 형태로 구할 수 있다. (확률밀도함수의 적분값이 1이 아니므로, 평균값을 구할 때 그 적분값을 나눠줘야 한다.)

$$\braket{E}_k = {(\int_0^\infty \frac{1}{2}m v^{2} e^{-\frac{1}{2}m v^{2}/k_{B}T} dv)}/{(\int_0^\infty e^{-\frac{1}{2}m v^{2}/k_{B}T} dv)} \\ = (\frac{1}{2} m \times \frac{1}{4} \sqrt{\frac{8\pi k_{B}^{3}T^{3}}{m^{3}}}) / (\frac{1}{2} \sqrt{\frac{2\pi k_{B}T}{m}}) = \frac{1}{2}k_{B}T$$

$$\braket{E}_p = {(\int_0^\infty \frac{1}{2}k x^{2} e^{-\frac{1}{2}k x^{2}/k_{B}T} dx)}/{(\int_0^\infty e^{-\frac{1}{2}k x^{2}/k_{B}T} dx)} \\ = (\frac{1}{2} k \times \frac{1}{4} \sqrt{\frac{8\pi k_{B}^{3}T^{3}}{k^{3}}}) / (\frac{1}{2} \sqrt{\frac{2\pi k_{B}T}{k}}) = \frac{1}{2}k_{B}T$$

$$\braket{E} = \braket{E}_k + \braket{E}_p = \frac{1}{2}k_{B}T + \frac{1}{2}k_{B}T = k_{B}T$$

평균 에너지도 이제 다 구했으니, 공식에 얼른 넣어보자.

$$ dE(\nu, T) = \rho (\nu, T)d\nu = \frac{8\pi \nu ^{2}}{c^{3}} \braket{E}d\nu = \frac{8\pi \nu ^{2}k_{B}T}{c^{3}}d\nu$$

위 식을 Rayleigh-Jeans의 흑체 복사 법칙이라고 한다. 이제, 흑체 복사 법칙을 구했으니, 파장에 따른 복사 세기 그래프를 그려보자.

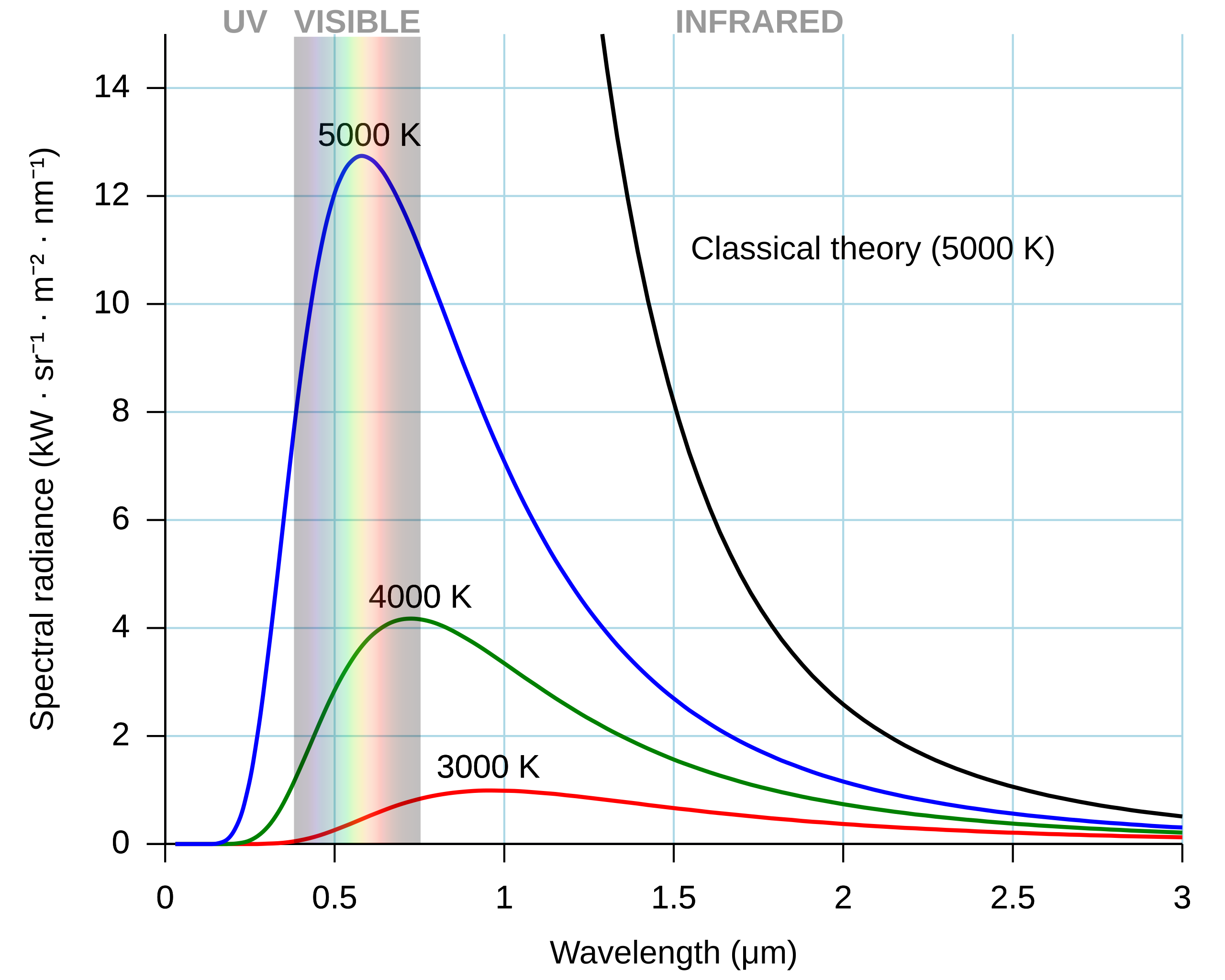
위 그래프에서 파란색 선은 실험을 통해 얻어진 5000K인 흑체에서 파장별 흑체 복사 세기이고, 위에서 무시하라고 했었던 검은색 선(Classical Theory)이 Rayleigh-Jeans의 흑체 복사 법칙을 그래프로 도시한 결과이다. 잘 살펴보면 장파장대, 즉 진동수가 낮은 영역에서는 Rayleigh-Jeans의 흑체 복사 법칙이 실제 측정값과 잘 맞지만, 단파장대(진동수가 높은 영역)에서는 Rayleigh-Jeans의 흑체 복사 법칙에 따른 복사 세기가 무한대로 발산해버린다!! 다시 말해서, Rayleigh-Jeans의 흑체 복사 법칙은 단파장에서 복사선의 세기를 잘 설명하지 못한다. 이를 자외선 파탄(Ultraviolet Catastrophe)라고 한다.

Planck의 에너지 양자화 가설과 Planck 복사 법칙

막스 플랑크는 위 자외선 파탄 현상을 보고, 놀라운 통찰력을 발휘해 다음과 같은 생각을 했다.

정상파 수 밀도 유도 과정은 틀린 게 없더라...
뭔가 에너지가 연속적이라는 가정 때문에 문제가 발생하는 것 같은데? 에너지가 불연속적이라고 한번 놓고 식을 구해보자.

따라서, 막스 플랑크는 다음과 같은 에너지가 불연속적으로 양자화되었다는 식을 제시했다. 이를 Planck의 에너지 양자화 가설이라고 한다.

$$E=nh\nu\;(단,\;n은\;음이\;아닌\;정수)$$

위 양자화 가설에 입각하여 평균 에너지를 다시 구해보자. 에너지가 불연속적으로 바뀌었으므로, 적분 대신에 급수를 활용하여 구해주어야 한다.

평균 에너지는 입자의 전체 에너지를 입자의 수로 나눠준 값이므로, 입자의 전체 에너지($E_{tot}$)와 입자의 수($N_{tot}$)를 각각 구해보자.

$$\begin{aligned}
N_{tot}
&= \lim_{i \to \infty}(N_{0} + N_{1} + N_{2} + ... + N_{i}) = \sum_{i=0}^{\infty} N_{i} \\
&= \sum_{i=0}^{\infty} N_{0} e^{-ih\nu/k_{B}T} = \sum_{i=0}^{\infty} N_{0} {(e^{-h\nu/k_{B}T})}^{i} = \frac{N_{0}}{1- e^{-h\nu/k_{B}T}}
\end{aligned}$$

전체 에너지를 구할 때는 멱급수의 합을 활용해서 구해야 한다. (원래 에너지 식과 양변에 $e^{-ih\nu/k_{B}T}$를 곱한 식을 빼주면 된다.)

$$\begin{aligned}
E_{tot}
&= \lim_{i \to \infty}(E_{0} + E_{1} + E_{2} + ... + E_{i}) = \sum_{i=0}^{\infty} E_{i} \\
&= \sum_{i=0}^{\infty} N_{0}ih\nu e^{-ih\nu/k_{B}T} = \sum_{i=0}^{\infty} N_{0}h\nu i{(e^{-h\nu/k_{B}T})}^{i} \\
&= \frac{N_0 h\nu e^{-h\nu/k_B T}}{\left( 1 - e^{-h\nu/k_B T} \right)^2} \\
\end{aligned}$$

위에서 구한 전체 에너지와 입자의 수를 활용해 평균 에너지를 구하면 다음과 같다.

$$\braket{E} = \frac{E_{tot}}{N_{tot}} = \frac{\frac{N_0 h\nu e^{-h\nu/k_{B}T}}{\left( 1 - e^{-h\nu/k_{B}T} \right)^2}}{\frac{N_{0}}{1- e^{-h\nu/k_{B}T}}} = \frac{h\nu e^{-h\nu/k_B T}}{1-e^{-h\nu / k_B T}} =\frac{h\nu}{e^{h\nu/k_B T }- 1}$$

이제, 에너지 양자화 가설에 따른 평균 에너지를 구했으므로, 이를 흑체 복사 법칙 식에 넣어보자!

$$\begin{aligned}
dE(\nu, T)
&= \rho (\nu, T)d\nu = \frac{8\pi \nu^{2}}{c^{3}} \braket{E}d\nu = \frac{8\pi \nu^{2}}{c^{3}}\frac{h\nu}{e^{h\nu/k_B T }- 1} d\nu \\
&= \frac{8\pi h \nu^{3}}{c^{3}}\frac{1}{e^{h\nu/k_B T }- 1} d\nu
\end{aligned}$$

위 식을 Planck의 흑체 복사 법칙이라고 한다. ​고생해서 구한 Planck의 흑체 복사 법칙에 따른 그래프를 그려보니까, 실험 결과와 잘 맞았다!

사실 처음에 이 가설을 만든 과정은 그냥 끼워맞추기(?)에 불과했지만, 이 가정이 흑체 복사 현상을 가장 잘 모델링했기 때문에 "에너지가 불연속적이다"라는 아이디어가 받아들여졌고, 이를 통해 "이산적인 양자 세계"를 처음으로 인식하게 되었다.

참고 자료

• Oxtoby, D. W., Gillis, H. P., Campion, A., & Butler, L. J. (2016). Principles of modern chemistry (7th ed.). Boston, MA: Cengage Learning.
• Atkins, P. W., de Paula, J., & Keeler, J., Atkins’ Physical Chemistry, 8th ed., Oxford University Press, 2018.
• Beiser, A. (2003). Concepts of modern physics (6th ed.). McGraw-Hill.
• 위키백과 - 흑체 (https://ko.wikipedia.org/wiki/%ED%9D%91%EC%B2%B4#HeroSection)