속보) 물질도 빛과 같은 파동임으로 밝혀져.. 일동 충격
저번 글에서 우리는 광전 효과에서 발견된 여러 고전역학의 모순들을 해결해준 광양자설을 살펴보았다. 광양자설에서 빛은 각각 $E=h\nu$의 에너지를 가지는 광자의 다발로 이루어져있고, 빛은 입자의 특성을 가지고 있다. 결국 광양자설을 통해 파동의 물질성이 받아들여지게 된다.
그런데, 20세기 대학원생(!!!)이었던 루이 드 브로이(Louis de Broglie)의 천재적인 역발상을 통해 물질은 충격적이게도 파동의 특성을 띈다는 점이 규명된다. 이번 글에서는 물질의 파동성에 숨겨진 기묘하고 신기한 양자역학적 원리를 살펴보고, 양자역학의 핵심 가설 중 하나인 파동-물질 이중성을 알아보자.
드 브로이 물질파 이론
드 브로이는 아인슈타인의 놀라운 광양자설 논문을 열심히 읽어보다가 이런 생각을 하게 된다.
자연은 대칭적인걸 좋아하니까, 파동의 물질성이 있으면 물질의 파동성도 있으면 딱 맞을 거 같은데, 물질의 파동성이 없는게 너무 짜친다 ㅡㅡ
결국, 드 브로이는 참지 못하고 자신이 직접 물질의 파동성을 나타내는 이론을 만들기로 하고, 물질파 이론을 제시하게 된다.
드 브로이의 물질파 이론은 모든 물질은 파동적인 특성을 가진다고 말하는 이론이다. 다시 말해서, 빛 뿐만 아니라 전자, 심지어 축구공도 특정한 파장을 가지는 파동처럼 거동한다.
드 브로이 물질파 이론에서 드 브로이 파장(물질파의 파장)은 다음과 같이 주어진다.
$$\lambda = \frac{h}{p}$$
드 브로이 물질파 식의 유도
왜 하필 물질파의 파장은 $\frac{h}{p}$일까? 지금부터 그 이유를 파헤쳐보도록 하자.
물질파 얘기를 하기 전에 빛(파동)의 운동량과 파장의 관계식을 구해보자. 특수상대성 이론에서 알 수 있었던 상대론적 에너지 식은 다음과 같다.
$$E ^{2} = (pc) ^{2} + (mc ^{2}) ^{2} = (pc) ^{2} + (E_{0}) ^{2}$$
일반적으로, 광자의 질량은 0임이 알려져 있으므로, 정지 에너지 항을 없애주면 광자의 운동량과 에너지 사이 관계는 다음과 같다.
$$E = pc$$
광양자설에서 보았듯, 광자 하나의 에너지에 대해 $E=h\nu$가 성립한다. 이를 위 식에 대입한 뒤 잘 정리해주면 다음과 같이 파동의 운동량과 파장의 관계식이 나오게 된다.
$$h\nu = h \frac{c}{\lambda} = pc$$
$$p = \frac{h}{\lambda}$$
드 브로이는 위 관계식이 광자 뿐만 아니라 일반적인 입자에서도 성립한다고 가정하고(물질의 파동성), $\lambda$와 $p$의 자리를 바꾸어 주어 다음과 같은 드 브로이 물질파 식을 유도하였다.
$$\lambda = \frac{h}{p}$$
잠깐, 눈을 크게 뜨고 찾아보면 이상한 점이 있다. 위에서 광자의 질량은 0이라 두고 식을 유도하였지만, 실제 물체에 대해 물질의 질량은 0이 아니라서 모순이 발생한다. 이에 대한 드 브로이의 답은 다음과 같다.
아몰랑~
실제로, 위 유도 과정에서 질량을 가지고 있는 입자에 대해서도 정지 질량 항을 무시해도 되는 이유는 현대 양자물리학에서도 설명을 못하고 있는 난제이다. 그러나, 후술할 데이비슨-거머 실험 등 실제 측정 결과와 매우 잘 맞기 때문에 그냥 받아들인 채로 위 식을 사용하고 있다.
데이비슨-거머 실험
지금까지 드 브로이 물질파 이론은 그냥 귀족 도련님의 억지 주장처럼 보였다. 그러나, 데이비슨-거머 실험의 결과가 발표된 이후에 바로 전세가 역전되며 정설로 받아들여졌다.
1927년, 클린턴 데이비슨과 레스터 거머는 니켈 금속(Ni)의 결정을 분석하기 위하여금속에 전자빔을 막 쏘아대고 있었다. 특히, 파장이 길어야 전자 회절이 잘 되므로 54eV의 낮은 에너지로 전자를 가속시켜 전자를 쏘았다. 그러다가, 전자총으로부터 50º 위치로 전자가 가장 많이 산란되는 것을 발견하였다. (아래 그림의 실험 결과 그래프는 극좌표처럼 원점으로부터 떨어진 거리가 클수록 튀어나온 전자 수가 많다고 읽으면 된다.)
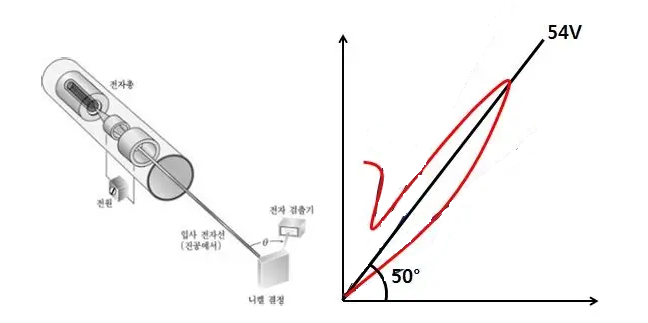
두 과학자는 전자총과 50º의 위치에서 아래 그림과 같이 일종의 보강간섭이 일어나 관측된 전자의 수가 가장 많다고 해석하였다.
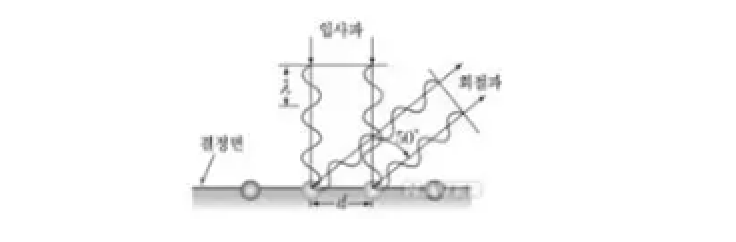
실험 결과를 해석하기 위하여, 두 물리학자는 광학에서 배웠던 보강 간섭 조건을 활용해 전자의 파장을 구하였다. 위 그림에서 두 회절파의 경로차 $\Delta = d \mathrm{sin} 50 ^\circ$이기 때문에, 이를 보강간섭이 일어날 조건($\Delta = n\lambda$, n은 정수)에 대입하면 다음과 같다. (여기서 두 회절파가 바로 인접해 있으므로, n=1로 넣고 계산하였고, d에는 알려진 니켈 결정 간 간격을 대입하였다.)
$$\Delta = d \mathrm{sin} 50 ^\circ = 1\times\lambda$$
$$\lambda = d \mathrm{sin} 50 ^\circ = 215 \, \mathrm{pm} \times \mathrm{sin} 50 ^\circ \approx 165 \, \mathrm{pm}$$
이제, 드 브로이 물질파 이론을 활용해 드 브로이 물질파 파장을 구해보자. 운동에너지 공식 $E_{k} =\frac{p ^{2}}{2m}$ 식과 에너지 보존 식을 활용하여 전자의 운동량을 구하였다.
$$eV = E_{k} =\frac{p ^{2}}{2m}$$
$$\therefore p = \sqrt{2meV}$$
따라서, 전자의 드 브로이 파장은 다음과 같다.
$$\lambda = \frac{h}{\sqrt{2meV}} \approx 167 \, \mathrm{pm}$$
헐! 전자의 드 브로이 파장과 실험 결과로 측정된 파장이 거의 같다. ㄷㄷㄷ
이를 통해, 드 브로이 물질파 이론이 데이비슨-거머 실험의 결과를 잘 설명해 주어서, 물질파 이론이 학계에서 받아들여지게 되었다.
파군, 위상속도와 군속도
위에서 드 브로이가 전자, 축구공 등 모든 물질은 파동성을 띈다고 제안하였다. 그러나, 실제 물질을 사인파($y= \mathrm{sin} x$)나 사각파와 같은 단일 파동으로 해석하면 이상한 점이 있다.
바로, 내가 보고 만지는 물건은 어느 한 곳에 국소화되어 위치하고 있는데, 단일 파동은 공간 전체에 비슷한 진폭으로 퍼져 있어서 이를 설명하지 못한다. 이 문제를 해결하기 위해서, 물리학자들은 다음과 같은 생각을 떠올렸다.
맥놀이 현상에서 파장이 살짝 다른 두 파동을 중첩시켰을 때, 아래 그림과 같이 포락선 안에 파동이 진동하고 있는 형태가 나타났어. 이거랑 비슷하게, 여러 파동을 무한히 중첩시키면 포락선의 형태로 국소화된 "파동 묶음"이 만들어지지 않을까?
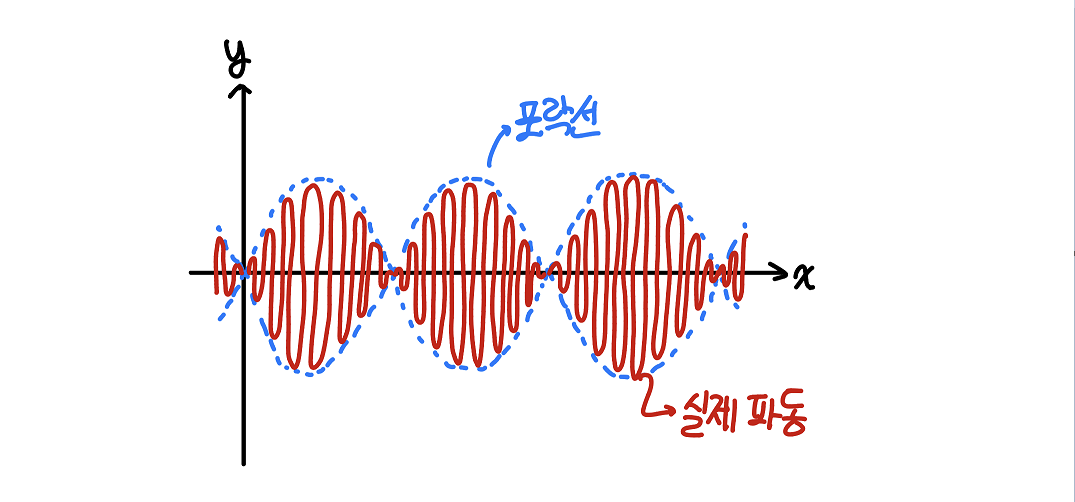
그래서 물리학자들은 여러 파동을 중첩시켜 보았고, 가우스 함수 따라 진폭을 가지는 파동을 무한 개 중첩시키면 다음과 같이 국소화된 파동이 얻어짐을 알 수 있었다.
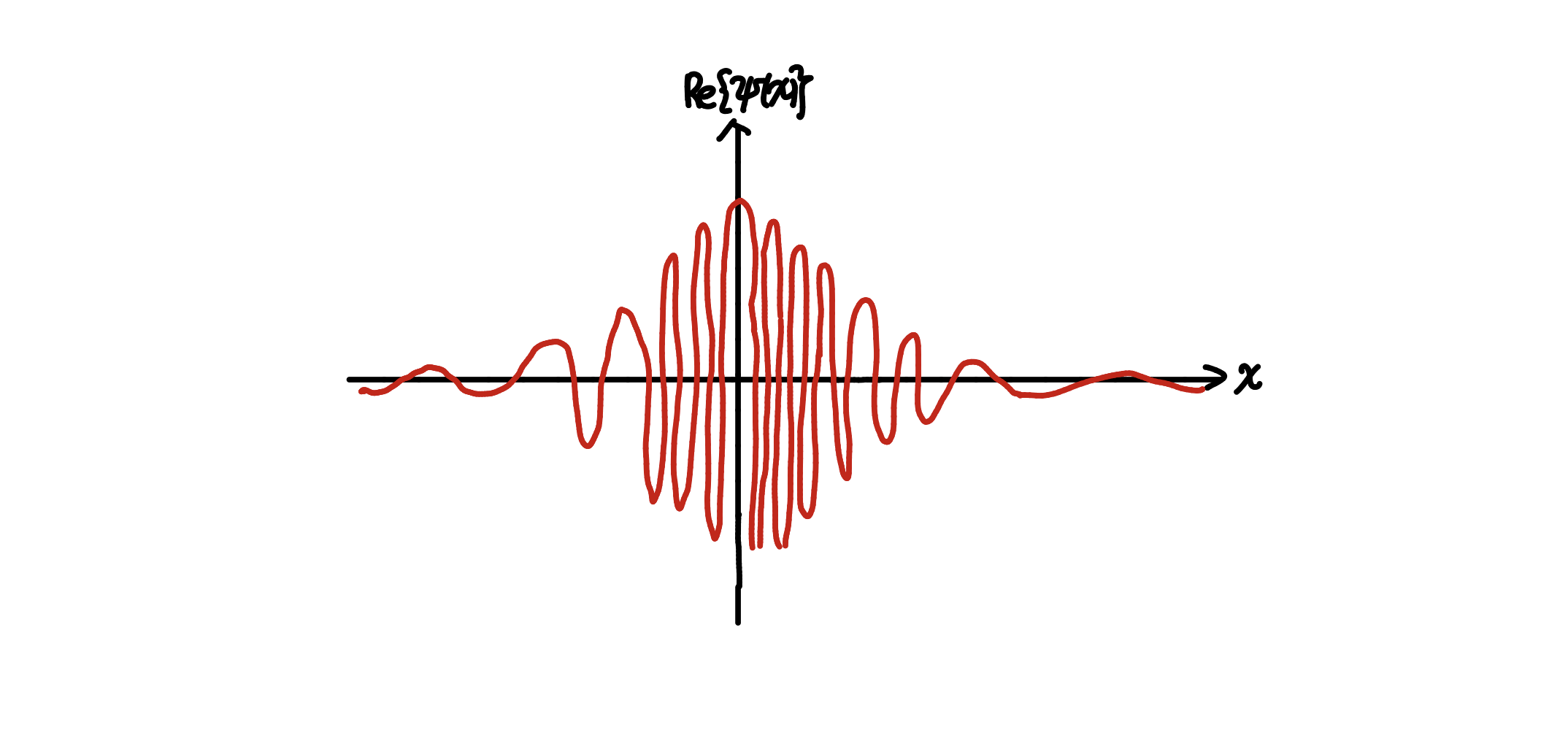
와우! 딱 봐도 $x=0$ 축 근처에 몰려 있는(국소화된) 파동이 만들어졌다. 이처럼 파동 여러개를 중첩시키는 방법으로 물질파의 국소성 문제를 해결하였다.
파군에서 여러 파동을 중첩시킨 일종의 "파동 그룹"을 파군이라고 한다. 또한, 물질을 파동으로 보았을 때 포락선 속 파동 각각의 진행 속도를 위상속도(Phase Velocity, $v_{p}$)라고 하며, 포락선의 속도, 다시 말해서 물질파의 전체적인 진행 속도를 군속도(Group Velocity, $v_{g}$)라고 한다. 실제 우리가 말하는 물질의 속도는 물질파의 전체적인 속도인 군속도를 의미한다.
파동에 두 가지 속도가 어떻게 존재하는지 잘 이해되지 않는 독자는 아래 영상을 보고 넘어가자. 아래 영상은 두 진폭이 같은 파동을 중첩한 파군이 진행하는 모습을 담고 있다. 포락선 속 파동의 끝자락을 잘 살펴보면, 군속도에 따른 파군의 전체적인 진행과는 상관없이 진폭이 조금씩 요동치면서 위상속도에 따라 진행하고 있음을 알 수 있다.
그러면, 일반적인 파동과 물질파의 위상속도와 군속도를 구해보자. 파동의 속력 $v = \nu \lambda$가 성립한다. ($v = f \lambda$랑 같은 말) 여기서, 적절히 문자 변환을 해서 진동수를 각진동수로, 파장을 파수로 바꿔주면, 파동의 위상속도는 다음과 같다는 점을 쉽게 알 수 있다.
$$v_{p} = \nu \lambda = 2\pi\nu \times \frac{\lambda}{2\pi} = \frac{\omega}{k}$$
이제, 이 공식을 물질파의 상황에 적용해보자. 플랑크의 에너지 양자화 가설 $E=h\nu$, 드 브로이의 물질파 이론 식인 $\lambda = \frac{h}{p}$ 식을 적용하면, 다음과 같은 관계를 얻을 수 있다.
$$ v_ {p} = \frac{\omega}{k} = \nu\lambda = \frac{ h\nu}{\frac{h}{\lambda}} = \frac{E}{p} $$
특수 상대성 이론에서 상대론적 에너지 $E=\gamma m c ^{2}$, 상대론적 운동량 $p=\gamma m v$ 식을 대입해주자. 그러면, 다음과 같이 물질파의 위상 속도가 구해진다.
$$ v_ {p} = \frac{E}{p} = \frac{c ^{2}}{v} > c \,\, (???)$$
어떻게 보면, 물질의 속력 v는 광속보다 빠를 수 없으므로, 물질파의 위상 속도 $v_{p}$가 광속 c를 넘어 특수 상대성 이론에 정면으로 모순되는 것 처럼 생각할 수도 있다. 그러나, 실제로 물질에 관한 정보를 전달하는 것은 각각의 파동이 아니라 전체적인 파동인 포락선이기 때문에, 위상 속도가 c를 넘는 것은 특수 상대성 이론에 위배되지 않는다. (다시 말해서, 위상속도는 물리적인 실체의 속도가 아닌 파동 기하학적인 속도일 뿐이다.)
이제, 군속도를 구해보자. 군속도를 구하기 위하여 파군을 구해야 하므로, 일단 다음과 같이 진폭이 같으며, 파수와 각진동수가 각각 $\Delta k$, $\Delta \omega$만큼 차이나는 두 파동의 결합에 대해서 생각해보자.
$$y_{1} = A\mathrm{sin} (kx - \omega t), \, y_{2} = A\mathrm{sin} ((k+\Delta k) x - (\omega + \Delta \omega )t)$$
파군의 진폭 $Y$를 두 파동을 더해 구해보자. 이 과정에서 삼각함수의 합을 곱으로 바꾸는 공식 $\mathrm{sin} A + \mathrm{sin} B = 2\mathrm{sin} (\frac{A+B}{2}) \mathrm{cos} (\frac{A-B}{2})$을 사용하였다.
$$\begin{aligned}
Y
&= y_{1} + y_{2} = A\mathrm{sin} (kx - \omega t) + A\mathrm{sin} ((k+\Delta k) x - (\omega + \Delta \omega )t) \\
&= 2A \mathrm{sin} ((k + \frac{\Delta k}{2})x - (\omega + \frac{\Delta \omega }{2})t) \;\mathrm{cos} (\frac{\Delta k}{2}x - \frac{\Delta \omega }{2}t) \\
&= [2A\mathrm{cos} (\frac{\Delta k}{2}x - \frac{\Delta \omega }{2}t)] \; \mathrm{sin} ((k + \frac{\Delta k}{2})x - (\omega + \frac{\Delta \omega }{2})t)
\end{aligned}$$
여기서, 앞에 대괄호로 묶은 항이 포락선이다. 실제로, 위 그래프를 Desmos 그래프 그려주는 툴로 그리면 다음과 같은 그래프가 나온다.
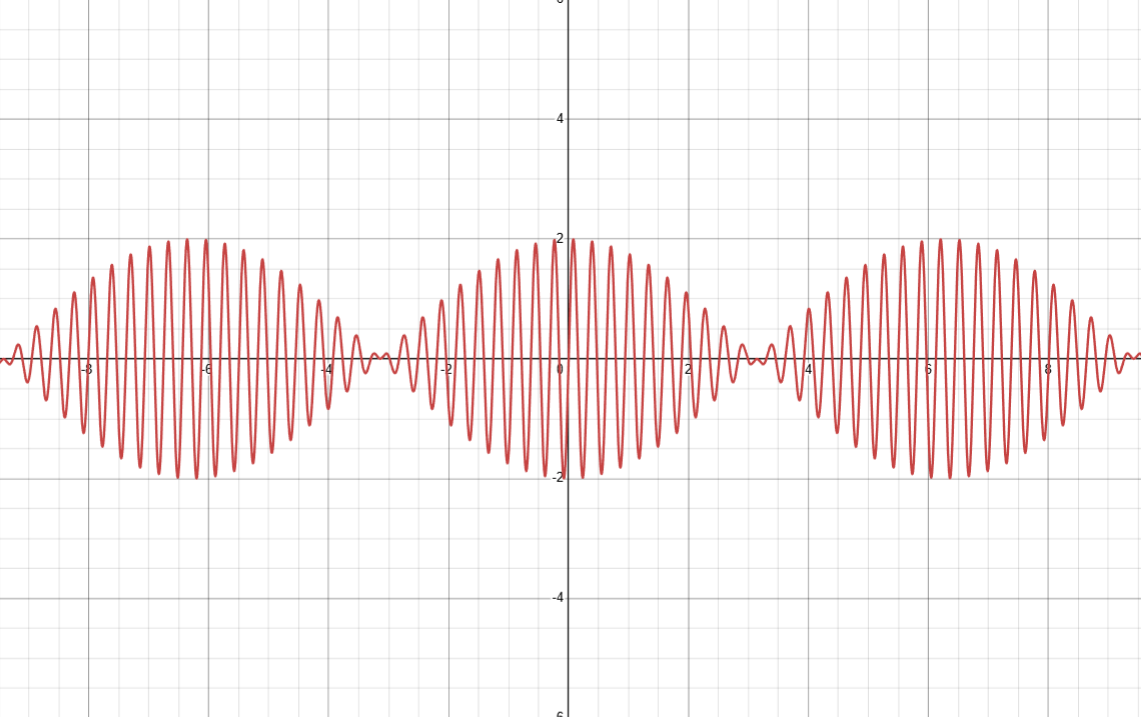
위에서 보았던 파동의 속력 공식 $v = \lambda \nu = \frac{\omega }{k}$를 활용하면, 같은 진폭 파동 2개를 중첩시킨 상황에서의 포락선의 속력인 군속도를 다음과 같이 구할 수 있다.
$$v_{g} = \frac{\Delta \omega }{\Delta k}$$
파동의 수가 무한개가 되면, 각 파동 사이 각진동수와 파수값의 차이 $\Delta \omega $, $\Delta k$ 값은 무한히 작아지게 되고, 따라서 미소 변화량 $d\omega $, $dk$로 각각 근사할 수 있다. 이를 적용하면, 파동의 군속도 공식은 다음과 같다.
$$v_{g} = \frac{d\omega }{dk}$$
이제, 물질파의 군속도를 구해 보자. 위상 속도 구할 때 문자 변환했던거랑 비슷하게 $E=h\nu$, $p = \frac{h}{\lambda}$ 공식을 넣어주면 다음과 같다.
$$ v_ {g} = \frac{d\omega }{dk} = \frac{d(2\pi \nu)}{d(\frac{2\pi}{\lambda})} = \frac{d(h\nu)}{d(\frac{h}{\lambda})} = \frac{dE}{dp} $$
상대론적 에너지 $E=\gamma m c ^{2} = \frac{c}{\sqrt{c ^{2} - v ^{2}}} m c ^{2}$, 상대론적 운동량을 $p = \gamma m v = \frac{c}{\sqrt{c ^{2} - v ^{2}}} m v $ 식을 넣어주고, v에 대해 미분해 식을 정리하자.
$$v_{g} = \frac{dE}{dp} = \frac{dE / dv}{dp / dv}$$
$$\frac{dE}{dv} = m v \left(1-\frac{v ^2}{c ^2}\right) ^{-3/2}$$
$$\frac{dp}{dv} = m\left(1-\frac{v ^2}{c ^2}\right) ^{-3/2}$$
$$\therefore v_{g} = \frac{dE / dv}{dp / dv} = v$$
직접 구해 보니, 물질파의 군속도는 물질의 속력과 같아 c보다 작기 때문에, 특수 상대성 이론을 위반하지 않음을 알 수 있다.
수식의 남발에 지친 여러분을 위해 이 파트에서 알아본 내용을 정리해보자.
물질파를 기술할 때 물질이 어떤 위치 범위에 국소화됨을 반영하기 위하여 여러 파동의 합인 파군을 활용하며, 물질파 속 파동 각각의 속도를 위상속도라 하고, 물질파의 전체적인 속력을 군속도라 한다. 일반적인 파동의 위상속도와 군속도는 다음과 같다.
$$v_{p} = \frac{\omega }{k}, \, v_{g} = \frac{d\omega }{dk}$$
그리고, 드 브로이 물질파의 위상속도와 군속도는 다음과 같다.
$$v_{p} = \frac{c ^{2}}{v}, \, v_{g} = v$$
파동-입자 이중성
앞의 광양자설에서부터 빛은 파동성과 입자성을 동시에 띄는 파동의 입자성을 알 수 있었고, 위의 물질파 이론으로부터 모든 입자는 파동성을 가진다는 입자의 파동성을 알 수 있다.
결국 우리는 이렇게 결론내릴 수 있다.
자연계의 모든 존재는 입자와 파동의 성질을 동시에 지니고 있다.
이것이 바로 양자역학을 지탱하는 핵심 가설 중 하나인 파동-입자 이중성이다.
실제로, 파동-입자 이중성을 실험적으로도 확인할 수 있다. 전자의 이중 슬릿 실험에서 입자인 전자를 하나씩 쏘았음에도 불구하고, 스크린에서는 마치 두 물질파가 간섭한 결과와 비슷하게 회절 무늬가 나타난다. 이를 통해 우리는 전자가 마치 파동처럼 거동한다는 것을 알 수 있고, 결국 "파동-입자 이중성"이라는 하나의 답으로 귀결됨을 밝힐 수 있었다.
결론
이번 글에서 우리는 드 브로이의 물질파 이론을 바탕으로 물질의 파동성을 살펴보았고, 파동-입자 이중성을 통해 모든 물체는 파동성과 입자성을 동시에 띔을 알아보았다. 이를 통해, 우리는 고전역학의 이분법적인 사고에서 벗어나서 양자역학의 중첩성에 발을 들이게 되었다!
다음 글에서는 이 물질파를 나타내는 파동함수와, 이 파동함수에서 물리적으로 유의미한 값을 뽑아내는 연산자에 관해 알아보자.
참고 자료
- Oxtoby, D. W., Gillis, H. P., Campion, A., & Butler, L. J. (2016). Principles of modern chemistry (7th ed.). Boston, MA: Cengage Learning.
- Atkins, P. W., de Paula, J., & Keeler, J., Atkins’ Physical Chemistry, 8th ed., Oxford University Press, 2018.
- Beiser, A. (2003). Concepts of modern physics (6th ed.). McGraw-Hill.
- Serway, R. A., & Jewett, J. W. (2018). Physics for scientists and engineers (10th ed.). Cengage Learning.
연습문제
연습문제는 다음 주에 올라옵니다!
(힝 속았지?)






Comments ()