파동함수, 모든 물질의 발자취
우리는 지지난 글부터 지난 글까지 두 편에 걸쳐서 파동-물질 이중성에 관하여 살펴보았다. 파동-물질 이중성이란 파동과 물질은 서로 동등한 존재며, 자연계의 모든 존재는 입자와 파동의 성질을 동시에 지니고 있다는 매우 중요한 가설이었다.
이 가설에 의해, 양자역학에서는 모든 물질을 파동인 물질파로 해석하게 된다. 그리고, 물리학자들은 이 "물질파"를 나타내는 수학적인 함수를 만들게 되는데, 이를 파동함수라고 한다.
이번 글에서는 파동함수와, 파동함수에서 물리적으로 유의미한 값을 뽑아내는 연산자에 관해 알아보자.
글을 시작하기 전에...
지금까지는 양자역학이 탄생하게 된 배경에 관해 살펴보았기 때문에 사실 내용을 이해 못한다고 해서 뒷 글 내용에 문제가 생기진 않았다. 그러나, 이번 글은 진짜 양자역학/양자화학의 산으로 등산을 떠나기 위해 운동화, 로프 등 준비물을 챙기는 셈의 글이기 때문에, 매우 중요하고, 길고, 어렵다.
이 글 내용이 재미있으면 그래도 꾹 참고 읽어볼 텐데, 수학적인 도구를 늘어놓는 내용이기 때문에, 겁나 재미없다! 실제로 시리즈 글에 괴상한 드립을 늘어놓는 걸 좋아하는 필자도 이번 글에서 칠 드립이 없어서 매우 난감해하고 있다.
그렇다고 사칙연산을 모르면서 연립방정식을 풀 수는 없듯이 이번 글 내용을 놓친다면 앞으로 있을 글의 내용을 절대 이해하지 못한다. 그러므로, 특히 주의해서 차근차근 읽어보자.
(실제로 군론 초반부 글을 제외하고 모든 글에 "파동함수"라는 단어가 무조건 한번씩 언급될 정도다.)
물질파와 파동함수
양자역학에서 파동함수란 파동을 기술하기 위한 함수로, 입자의 동적인 특성에 대해 얻을 수 있는 모든 정보를 포함한다. 파동함수는 고전역학에서 배웠던 아래 파동방정식의 해가 되는 함수이다.
$$\frac{\partial ^{2} y}{\partial x ^{2}} = \frac{1}{v ^{2}} \frac{\partial ^{2} y}{\partial t ^{2}}$$
특히, 양자역학의 맥락에서는 나중에 다룰 슈뢰딩거 방정식을 풀어서 나온 해를 의미하기도 한다. (일단 슈뢰딩거 방정식을 양자역학의 운동방정식이라고만 인식하고 넘어가자.)
$$i\hbar \frac{\partial \Psi}{\partial t} = (-\frac{\hbar ^{2}}{2m} \nabla ^2 + U)\Psi$$
보통 양자역학에서는 양자역학에서의 파동함수임을 강조하기 위해서 파동함수를 $y(x, t)$ 대신에 $\Psi (x, t)$(프사이)로 나타낸다. 그리고, 파동함수 $\Psi (x, t)$의 함숫값 그 자체는 물리적인 의미를 가지기보다는 그냥 그 위치에서 파동함수의 진폭을 의미한다.
행실 좋은 파동함수
제목만 들어도 너무 웃기다. 행실이 좋은 파동함수라니.. 놀랍게도 정식 용어다!
행실 좋은 파동함수란 양자역학적에서 물리적 의미가 있는 파동함수를 말한다. 행실 좋은 파동함수가 되기 위해서는 $\Psi$와 $\frac{\partial \Psi}{\partial x}$가 모든 곳에서 연속인 함수여야 하고, 규격화 가능해야 한다($\lim_{x \to \pm \infty} \Psi = 0$).
행실이 좋지 않은 파동함수의 예시는 다음과 같다.

양자역학 파동함수의 의미
앞에서도 봤듯이 양자역학이란 "어? 왠진 모르겠지만 이렇게 하면 어쨌든 잘 돌아가네"라는 생각으로 성립된 학문이기 때문에, 양자역학의 "본질"에 관해서 바라보는 관점이 정해져 있지 않고, 여러 가지가 있다.
그 중 가장 정설로 받아들여지는 양자역학의 해석 중 하나인 코펜하겐 해석에서는 파동함수가 입자가 존재하기 위한 확률을 계산하기 위한 수학적 도구로, 그 자체로는 의미를 가지지 않는다고 본다. 그리고, 어떤 물질을 측정하게 되면 그 물질을 기술하는 파동함수가 '붕괴'되며, 그 물질의 파동함수는 중첩 상태가 아닌 하나의 상태로만 결정된다고 해석한다.
고전역학적 파동함수와 파동함수의 성질
보른의 해석 - 확률밀도함수로서의 파동함수
막스 보른(Max Born)은 파동함수의 절댓값(norm) 제곱($|\psi| ^{2}$)이 입자가 특정 위치에 존재할 확률을 나타내는 확률밀도함수 $\rho$라고 해석하였다. 이를 보른의 해석이라고 한다.
$$|\psi| ^{2} = \psi ^{*} \psi = \rho (x, t)$$
(여기서, $\psi ^{ *}$는 $\psi$의 켤레복소수를 의미한다. 그리고, $|\psi| ^{2}$에서 $\psi ^{ *}$와 $\psi$의 순서가 매우 중요하며, 순서를 바꾸어 적으면 절대로 안 된다!)
보른의 해석에 따르면, 입자를 특정 범위 [a, b]에서 발견할 확률은 다음과 같이 계산할 수 있다.
$$P(a \le x \le b) = \int_{a}^{b} |\psi| ^{2} dx$$
보른이 이 해석을 이끌어낸 과정을 살펴보자. 일단, 대표적인 파동인 빛의 관점에서 살펴보면, 주어진 시공간에서 단위 부피당 광자 하나를 찾을 확률(P)은 단위 부피당 광자 수에 비례한다.
$$P \propto \frac{N}{V}$$
광양자설에 따르면, 전자기파(빛)의 세기 I는 단위 부피당 광자의 수에 비례한다.
$$P \propto \frac{N}{V} \propto I$$
또한, 전자기파의 세기 I는 전자기파의 진폭 E의 제곱에도 비례하기 때문에, 다음과 같이 적을 수 있다.
$$P \propto \frac{N}{V} \propto I \propto E ^{2}$$
따라서, 단위 부피당 광자 하나를 찾을 확률은 전자기파의 진폭의 제곱에 비례하게 된다.
$$P \propto E ^{2}$$
보른은 이 사실을 일반적인 물질파에도 적용하였다. 파동함수는 물질파의 진폭을 나타내므로, 결론적으로, 단위 부피당 물질을 찾을 확률은 파동함수의 진폭의 제곱에 비례하게 된다. 그러므로, 보른은 파동함수의 절댓값 제곱을 확률밀도함수로써 보았다.
규격성과 규격화
보른의 해석에 따르면, 파동함수 절댓값의 제곱은 입자가 특정 위치에 존재할 확률밀도함수의 의미를 갖는다고 하였다.
잠깐, 확률과 통계 시간때 배웠던 확률밀도함수의 성질을 되새겨보자. 확률의 총합은 1이 되어야 하므로, 파동함수의 절댓값 제곱의 전 영역을 적분한 값(=확률의 총 합)이 1이 되어야 한다. 이 성질을 파동함수의 규격성(또는 정규성, Normality)이라고 하며, 파동함수에 특정한 상수(이 상수를 규격화 상수라고 한다.)를 곱하는 등의 방법으로 정규성을 만족하도록 만드는 것을 규격화(또는 정규화, Normalization)라고 한다. 이를 수식으로 다시 쓰면 다음과 같다.
$$\int_{-\infty}^{\infty} |\psi|^2 dx = 1$$
직교성
위에서는 서로 같은 파동함수끼리 곱의 전 구간에서 적분값은 1임을 알아보았다. 그러면, 서로 다른 파동함수끼리 곱한 뒤 적분하면 어떻게 될까?
놀랍게도 0이 된다! 더 정확하게는, 특정 퍼텐셜 상태에서 특정 연산자의 서로 다른 두 고유함수에 대해, 한 고유함수의 켤레복소수와 다른 고유함수를 곱한 뒤 전 영역에서 적분한 값이 0이다. 이 성질을 파동함수의 직교성(orthogonality)이라고 한다. 이를 수식으로 다시 적으면 다음과 같다.
$$\int_{-\infty}^{\infty} \psi_{m} ^{ *} \psi_{n} dx = 0 \, (단, \; m \ne n)$$
여기서, 두 함수 f, g가 다음과 같은 식을 만족하면 두 함수 f, g는 직교한다고 한다.
$$\int_{-\infty}^{\infty} f ^{ *} g dx = 0$$
중첩의 원리
위에서 볼 수 있었듯, 파동함수는 아래 파동 방정식을 만족한다.
$$\frac{\partial ^{2} y}{\partial x ^{2}} = \frac{1}{v ^{2}} \frac{\partial ^{2} y}{\partial t ^{2}}$$
여기서, 파동 방정식이 2차 선형 미분 방정식이기 때문에, 서로 다른 파동 방정식의 해를 선형 조합한 함수 또한 파동 방정식을 만족하게 된다. 이를 중첩의 원리라고 하며, 이를 수식으로 다시 써 보면 다음과 같다.
$$\frac{\partial ^{2} y_{1}}{\partial x ^{2}} = \frac{1}{v ^{2}} \frac{\partial ^{2} y_{1}}{\partial t ^{2}}, \, \frac{\partial ^{2} y_{2}}{\partial x ^{2}} = \frac{1}{v ^{2}} \frac{\partial ^{2} y_{2}}{\partial t ^{2}}$$
$$\therefore Y := Ay_{1} + By_{2} \rightarrow \frac{\partial ^{2}Y}{\partial x ^{2}} = \frac{1}{v ^{2}}\frac{\partial ^{2}Y}{\partial t ^{2}}$$
파동함수의 복소수 표현
이제, 파동함수를 복소수의 형태로 기술하는 방법에 관해서 알아보자.
푸리에 급수(몰라도 됨)와 비슷한 방법으로, 파동은 sin, cos과 같은 파동함수로 나타낼 수 있다. 따라서, 한 방향으로 진행하고 물리적 실체를 가지는 파동함수의 일반적인 해는 중첩의 원리에 의해 다음과 같이 sin함수와 cos함수를 선형 조합한 것으로 나타낼 수 있다.
$$y=A {\rm sin} (kx-wt) + B {\rm cos} (kx-wt)$$
또한, 오일러 식($e^{i \theta } = {\rm cos} \theta + i {\rm sin} \theta $) 에 따라, 한 방향으로 진행하는 파동함수의 일반해는 다음과 같이 나타낼 수 있다. 지수함수가 삼각함수보다 적분이나 미분하기 훠어얼씬 쉽기 때문에, 우리는 이제부터 이 형태를 많이 사용한다. (허수 항이 보이지만 깔끔하게 무시해주자. 고전역학적으로는 어차피 물리적 의미가 없는 항이다.)
$$y=A e^{i(kx-wt)} = A {\rm cos} (kx-wt) + iA {\rm sin} (kx-wt)$$
우리에겐 앞으로 진행하는 파동뿐만 아니라 뒤로 진행하는 파동도 있기 때문에, 선형결합을 함으로써 양방향으로 진행하는 파동 모두 고려해 다음과 같이 파동함수의 일반해를 나타낼 수 있다.
$$\Psi (x, t) =A e^{i(kx-wt)} + B e^{-i(kx+wt)} $$
여기서, $kx \pm wt$ 항에 $\hbar$를 곱해주고 밖에 $\frac{1}{\hbar}$ 항을 빼 주면 파동함수의 일반해를 다음과 같이도 표현할 수 있다.
$$\Psi (x, t) =A e^{\frac{i}{\hbar}(px-Et)} + B e^{-\frac{i}{\hbar}(px+Et)}$$
연산자, 고윳값과 고유함수
자신이 알고 있는 연산을 아무거나 하나 떠올려보자. 필자의 머리 속에는 5를 곱하는 연산, 함수를 x에 대하여 2번 편미분하는 연산($\frac{\partial ^{2}}{\partial x ^{2}}$)이 생각났다. 일반적으로 연산자는 이와 같이 자신의 뒤에 따라오는 항에 어떤 연산을 해줄 것인지 알려주는 것을 말한다.
$p(x)=\mathrm{sin} 2x$에 $\frac{\partial ^{2}}{\partial x ^{2}}$ 연산자를 적용하면 $-4\mathrm{sin} 2x = -4p(x)$가 나오는 것 처럼 연산자를 적용하기 이전인 원래 함수의 상수배로 튀어나올 때가 있다. 이때, 함수에 곱해진 상수를 그 연산자에 의한 함수의 고윳값(eigenvalue)이라고 하고, 함수를 고유함수(eigenfunction)라고 한다. 연산자 $\hat{G}$에 의한 고유함수 $f$의 고윳값이 $G$라고 할 때, 다음과 같이 표현된다.
$$\hat{G} f = G f$$
위에서 언급했던 예시에 이 개념을 적용해 보면, $\frac{\partial ^{2}}{\partial x ^{2}}$ 연산자에 대해 $p(x)=\mathrm{sin} 2x$는 고유함수이며, 이 때 고윳값은 -4이다.
일반적으로, 연산자는 행렬과도 비슷해서 두 연산자의 순서를 바꾸면 다른 계산 결과가 나올 수도 있다. ($\hat{A}\hat{B} \ne \hat{B}\hat{A}$) 이렇게 두 연산자의 순서를 바꾸지 못한다면 두 연산자는 교환 불가능하다고 한다. 그러나, 단위행렬 I와 임의의 행렬 A의 관계처럼 일부 연산자는 서로 순서를 바꾸어도 같은 계산 결과가 나오는 경우가 있는데, 이 경우 두 연산자는 교환 가능하다고 한다.
따라서, 두 연산자의 교환 관계를 나타내는 연산자가 따로 있는데, 이를 교환자라고 하며, $[\hat{A}, \hat{B}]$로 표기한다. 교환자의 정의는 다음과 같다.
$$[\hat{A}, \hat{B}] = \hat{A}\hat{B} - \hat{B}\hat{A}$$
여기서, 교환자 값이 0이면 두 연산자는 교환 가능하고, 0이 아니면 두 연산자는 교환 불가능하다.
잠깐, 고윳값과 고유함수가 선형대수학에서 배운 고윳값과 고유벡터 개념과 비슷한 것 같다. 파동함수는 위에서 간단하게만 언급했던 (시간 비의존) 슈뢰딩거 방정식을 풀어서 나온 여러 기본적인 파동함수의 선형 결합으로 표현하고, 실제로, 이 기본적인 파동함수들은 힐베르트 공간이라는 벡터 공간의 기저(basis)를 이룬다. 그리고, 모든 파동함수는 힐베르트 공간 내의 벡터로 표현할 수 있으며, 연산자들은 이 벡터들에 곱하는 행렬로 표현할 수 있다. 사실 비슷하게 보였던 두 개념이 똑같은 개념인 것이었다!
(이렇게 행렬의 형태로 양자역학을 기술하는 것을 행렬역학이라고 한다. 사실 양자역학을 제대로 파기 위해서는 행렬역학에 대한 이해가 필수적이지만, 양자화학을 배우는 입장에서는 그렇게 깊게 들어갈 필요는 없어서 자세하게는 몰라도 된다.)
여러가지 연산자
위에서 볼 수 있듯이, 특정한 고유함수에 연산자를 적용하면 그 고윳값이 고유함수에 곱해진 형태로 나타난다. 그러면, 이 고윳값이 위치, 운동량, 에너지와 같이 물리적으로 의미가 있는 것이면 어떨까? 이번 파트에서는 자판기에서 버튼을 누르면 음료가 뽑아지는 것 같이 파동함수에서 물리량을 뽑아낼 수 있는 여러 연산자들에 대해 알아보자.
위치 연산자
파동함수의 위치 연산자는 $x$이다. 너무 당연하다. x 자체가 위치를 의미하는 변수이기 때문이다.
$$\hat{x} = x$$
운동량 연산자
운동량 연산자는 위치 연산자만큼 단순하지 않다. 입자의 운동량 $p=\gamma mv$를 위치와 시간의 사칙연산으로 나타내기 어렵기 때문이다.
일단, 파동함수의 일반해를 다시 살펴보자.
$$\Psi (x, t) =A e^{\frac{i}{\hbar}(px-Et)} + B e^{-\frac{i}{\hbar}(px+Et)}$$
잘 보면 지수 자리 속 x 앞에 p가 떡하니 있다! 일단 파동함수를 x에 관해 편미분해주어 이놈을 합성함수 미분법에 의해 앞으로 끌고 오자.
$$\frac{\partial \Psi}{\partial x} = A\frac{i}{\hbar}p e^{\frac{i}{\hbar}(px-Et)} + B\frac{i}{\hbar}p e^{-\frac{i}{\hbar}(px+Et)} = \frac{i}{\hbar}p \Psi$$
야호! p가 드디어 항복하고 파동함수에 곱해져 있는 형태로 나타났다. 고윳값을 p로 만들어주기 위해서 운동량 p 말고 다른 물리량을 좌변으로 넘겨주자.
$$\frac{\hbar}{i}\frac{\partial \Psi}{\partial x} = p \Psi$$
위 식을 다시 보면, $\frac{\hbar}{i}\frac{\partial }{\partial x}$라는 연산자를 파동함수에 적용하면 고윳값으로 운동량 p가 튀어나온다고 할 수 있다. 따라서, 우리는 $\frac{\hbar}{i}\frac{\partial }{\partial x}$을 운동량 연산자 $\hat{p}$라고 정의한다.
$$\hat{p} = \frac{\hbar}{i}\frac{\partial }{\partial x}$$
운동량 제곱 연산자
파동함수의 양변에 운동량 연산자를 두 번 취해주자.
$$\begin{aligned}
\hat{p}\hat{p}\Psi
&= \frac{\hbar}{i}\frac{\partial }{\partial x}\frac{\hbar}{i}\frac{\partial \Psi}{\partial x} = -\hbar^2 \frac{\partial^2 \Psi}{\partial x^2} \\
&= pp \Psi = p ^{2} \Psi
\end{aligned}$$
여기서, $-\hbar^2 \frac{\partial^2}{\partial x^2}$라는 연산자를 파동함수에 적용하면 고윳값으로 운동량의 제곱이 튀어나온다고 할 수 있다. 따라서, 우리는 $-\hbar^2 \frac{\partial^2}{\partial x^2}$를 운동량 제곱 연산자 $\hat{p^2}$라 정의한다.
$$\hat{p ^{2}} = -\hbar^2 \frac{\partial^2}{\partial x^2}$$
에너지 연산자
이제, 에너지를 뽑아주는 에너지 연산자를 구해보자. 파동함수의 일반해를 또 다시 살펴보면...
$$\Psi (x, t) =A e^{\frac{i}{\hbar}(px-Et)} + B e^{-\frac{i}{\hbar}(px+Et)}$$
에너지 E가 지수의 t 옆에 곱해져 있다. 위와 비슷한 방법으로 E를 밑으로 끌어내리기 위해 파동함수를 t에 관해 편미분해보자.
$$\frac{\partial \Psi}{\partial t} = -A\frac{i}{\hbar}E e^{\frac{i}{\hbar}(px-Et)} - B\frac{i}{\hbar}E e^{-\frac{i}{\hbar}(px+Et)} = -\frac{i}{\hbar}E \Psi = \frac{1}{i\hbar}E \Psi$$
우변에 $\Psi$에 곱해진 여러 상수들 중 에너지 E만을 남기고 나머지를 좌변에 넘기자.
$$i\hbar\frac{\partial \Psi}{\partial t} = E\Psi$$
또, 위 식을 보면 $ i \hbar \frac{\partial}{\partial t}$를 파동함수에 취하면 에너지가 튀어나온다. 따라서, 우리는 $ i \hbar \frac{\partial}{\partial t}$를 에너지 연산자 $\hat{E}$라 정의한다.
$$\hat{E} = i\hbar \frac{\partial}{\partial t}$$
해밀토니안 연산자
해밀토니안($H$)이란 해밀턴 역학(몰라도 됨)에서 동역학을 나타내는 함수로(몰라도 됨!!), 계의 고전역학적인 에너지를 의미한다. 고전역학에서 역학적 에너지 보존 법칙에 의해 계의 에너지는 퍼텐셜 에너지(위치 에너지) U와 운동 에너지 T의 합이며, 다음과 같이 나타낼 수 있다.
$$H = U + T$$
양변에 파동함수 $\Psi$를 살짝 곱해주자.
$$H\Psi = U\Psi + T\Psi$$
여기서, 운동에너지 $T = \frac{p ^{2}}{2m}$가 성립하므로, 다음과 같이 적을 수 있다.
$$H\Psi = U\Psi + \frac{p ^{2}\Psi}{2m}$$
음... 앞에서 보았던 운동량 제곱 연산자가 생각난다. 호딱 적용해주자.
$$H\Psi = U\Psi - \frac{\hbar ^{2}}{2m} \frac{\partial ^{2} \Psi}{\partial x ^{2}} = (-\frac{\hbar ^{2}}{2m} \frac{\partial ^{2} }{\partial x ^{2}}+ U)\Psi$$
이 식을 다시 보면, $-\frac{\hbar ^{2}}{2m} \frac{\partial ^{2} }{\partial x ^{2}}+ U$라는 연산자를 파동함수에 적용하면 고윳값으로 해밀토니안 H가 튀어나온다고 할 수 있다. 따라서, 우리는 $\frac{\hbar}{i}\frac{\partial }{\partial x}$을 해밀토니안 연산자 $\hat{H}$라고 정의한다.
$$\hat{H} = -\frac{\hbar ^{2}}{2m} \frac{\partial ^{2} }{\partial x ^{2}}+ U$$
Braket 표기
연산자 활용한 물리량의 기댓값
연산자를 활용하여 특정 값의 특정 구간에 대한 기댓값(평균값)을 구할 수도 있다. 확률과 통계 시간에 배웠듯이, 특정 물리량의 기댓값을 구하기 위해서는 특정 사건에서의 물리량 곱하기 그 사건의 확률을 싸그리 더해주면 된다. 따라서, 물리량 Q의 기댓값을 구하는 식을 적분을 활용해 다시 쓰면 다음과 같다.
$$E(Q) = \int_{b}^{a} Q P(x) dx$$
여기서 확률밀도함수 P(x)는 $|\Psi| ^{2}$과 같으며, $Q \Psi = \hat{Q} \Psi$ 식과 같이 물리량을 연산자로 바꿔 적을 수 있으므로, 다음이 성립한다.
$$\begin{aligned}
E(Q) &= \int_{b}^{a} Q P(x) dx = \int_{b}^{a} Q |\Psi| ^{2} dx = \int_{b}^{a} Q \Psi ^{*}\Psi dx = \int_{b}^{a} \Psi ^{*} Q\Psi dx \\
&= \int_{b}^{a} \Psi ^{*} \hat{Q} \Psi dx
\end{aligned}$$
특히, 전 영역에 대한 기댓값을 특별히 $\braket{Q}$(물리량의 기댓값임을 강조), $\braket{\hat{Q}}$(연산자 고윳값의 기댓값임을 강조)와 같이 꺾쇠괄호를 활용하여 나타낼 수도 있다.
$$\braket{Q} = \braket{\hat{Q}} = \int_{-\infty}^{\infty} \Psi ^{*} \hat{Q} \Psi dx = 1$$
Braket 표기법
양자역학에서 기댓값을 구하거나, 표준편차를 구하는 등의 상황에서 두 함수의 곱을 전 영역에서 적분할 일이 많은데, 이와 같이 어떤 함수의 켤레복소수와 다른 함수의 곱을 전 영역에서 적분한 값을 꺾쇠괄호 <>로 표기할 수 있다. 이를 Braket 표기법이라 하며, 다음과 같이 표기한다.
(두 함수의 내적과 비슷한 개념이다.)
$$\braket{f|g} = \int_{-\infty}^{\infty} f^{*} g dx$$
위에서, $\bra{f}$ 부분을 Bra라고 하며, $\ket{g}$ 부분을 ket라고 한다. 아쉽게도, Bra 또는 Ket 만을 따로 해석적으로 표현하는 방법은 없다. 다음과 같이 표현할 순 없잖아..
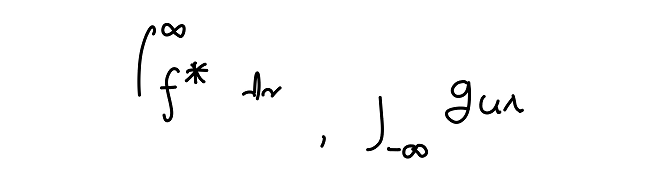
특별히, 위에서 보았던 $\braket{\hat{Q}} = \int_{-\infty}^{\infty} \Psi ^{*} \hat{Q} \Psi dx$를 braket 표기법으로 다시 표현해보면 $\braket{\Psi | \hat{Q} \Psi}$로 표기할 수 있다. 이로부터, $\braket{\hat{Q}}$는 Braket 표기법에서 $\bra{\Psi}$ 부분과 $\ket{\Psi}$ 부분이 생략된 것이라고 볼 수도 있다.
Braket 표기법을 활용하면 적분 기호 등을 직접 적지 않고도 전 영역에 관한 적분을 효과적으로 표현할 수 있어 표기가 간결해지는 장점이 있지만, 특정 구간에서 입자가 존재할 확률을 구할 수가 없다는 단점이 있다. (하지만, 양자역학에서 특정 구간에서 입자가 존재할 확률을 구하는 경우는 잘 없긴 하다.)
Hermitian 연산자
지금까지 양자역학의 연산자에 관하여 알아보았다. 그러면, 이런 질문을 하게 될 수 있다.
아무 연산자나 하나 잡았을 때, 그 연산자가 물리학적으로 의미를 가진다고 할 수 있을까?
이 질문에 대한 답은 "No!!! 아니다"이다. 더 자세히 말하면, 연산자가 물리학적인 의미를 가지기 위해서는 반드시 Hermitian 연산자여야 한다. 이 부분에서는 Hermitian 연산자에 대해 자세히 알아보고, Hermitian 연산자가 만족하는 여러 성질을 알아보도록 하자.
수반 연산자의 정의
두 연산자 $\hat{P}$, $\hat{Q}$가 다음 관계를 만족한다면, $\hat{P}$는 $\hat{Q}$의 수반(adjoint) 연산자(또는 Hermitian 켤레)라고 하며, $\hat{P}$를 $\hat{Q} ^\dagger$라고 표기한다.
$$\int_{-\infty}^{\infty} f^{*} \hat{Q}g dx = \int_{-\infty}^{\infty} (\hat{P}f)^{*} g dx \to \hat{P} = \hat{Q} ^\dagger$$
적분식만 보면 뭔 말인지 모르겠다. 이를 Braket 표기법을 활용해서 다시 표현해보자.
$$\braket{f|\hat{Q}g} = \braket{\hat{Q} ^\dagger f|g}$$
오! 다시 살펴보니 이항을 할 때 음의 부호가 붙는 것처럼, 연산자 $\hat{Q}$가 Braket 표기의 짝대기(|)를 넘어가면 그 수반 연산자 $\hat{Q} ^\dagger$로 바뀐다고 볼 수 있다.
그리고, 수반 연산자에 대해 다음 성질이 성립한다.
$$(\hat{Q} ^\dagger)^\dagger = \hat{Q}$$
Hermitian 연산자의 정의
특히, 자신의 수반 연산자가 다시 자신이 되는 연산자를 Hermitian 연산자(에르미트 연산자)라고 부른다. 이를 수식, 적분식, Braket 표기법으로 쓰면 각각 다음과 같다.
$$\hat{Q} ^\dagger = \hat{Q}$$
$$\int_{-\infty}^{\infty} f^{*} \hat{Q}g dx = \int_{-\infty}^{\infty} (\hat{Q}f)^{*} g dx$$
$$\braket{f|\hat{Q}g} = \braket{\hat{Q}f|g}$$
다시 말해서, Hermitian 연산자는 두 함수의 곱을 전 영역에 적분할 때, 어느 함수에 연산자를 적용하더라도 그 적분값이 같은 연산자를 말한다.
Hermitian 연산자의 성질
Hermitian 연산자는 다음과 같은 성질을 가진다.
- Hermitian 연산자에 의한 기댓값은 관측 가능한 값, 즉 실수이다.
- Hermitian 연산자에 의해 서로 다른 고윳값을 가지는 두 고유함수는 서로 직교한다.
이 두 성질 중 성질 1을 증명해보자.
Hermitian 연산자는 두 같은 함수 f에 대해 다음을 만족한다.
$$\int_{-\infty}^{\infty} f^{*} \hat{Q}f dx = \int_{-\infty}^{\infty} (\hat{Q}f)^{*} f dx$$
여기서, 좌변과 우변은 각각 다음과 같다.
$$\int_{-\infty}^{\infty} f^{*} \hat{Q}f dx = \int_{-\infty}^{\infty} Q f^{*}f dx = \braket{Q}$$
$$\int_{-\infty}^{\infty} (\hat{Q}f)^{*} f dx = \int_{-\infty}^{\infty} (Qf)^{*}f dx = \int_{-\infty}^{\infty} Q^{*}f^{*}f dx = \braket{Q^{*}}$$
좌변과 우변이 같기 때문에, 다음이 성립한다.
$$\braket{Q} = \braket{Q^{*}}$$
어떠한 값과 다른 값의 켤레복소수가 같으면 그 값은 실수이기 때문에 $\braket{Q}$는 실수임을 알 수 있다. 따라서, Hermitian 연산자에 의한 기댓값은 관측 가능한 값, 즉 실수이다.
물리적인 관측을 하여 기댓값을 얻었는데, 그 값이 실수가 아닌 것은 물리학적으로 말이 되지 않는다. 여기서, Hermitian 연산자에 의한 기댓값이 관측 가능한 값을 가지기 때문에, Hermitian 연산자는 파동함수에 적용되면 물리적으로 의미 있는 물리량을 뱉게 되고, 따라서 Hermitian 연산자는 물리적으로 의미 있는 연산자라고 말하는 것이다.
참고 자료
- Oxtoby, D. W., Gillis, H. P., Campion, A., & Butler, L. J. (2016). Principles of modern chemistry (7th ed.). Boston, MA: Cengage Learning.
- Beiser, A. (2003). Concepts of modern physics (6th ed.). McGraw-Hill.
- Serway, R. A., & Jewett, J. W. (2018). Physics for scientists and engineers (10th ed.). Cengage Learning.
- Griffiths, D. J., & Schroeter, D. F. (2018). Introduction to quantum mechanics (3rd ed.). Cambridge University Press.
- 코펜하겐 해석 - 위키백과 (https://ko.wikipedia.org/wiki/%EC%BD%94%ED%8E%9C%ED%95%98%EA%B2%90_%ED%95%B4%EC%84%9D)
연습문제
연습문제 양이 많아서 별도의 Appendix 글로 올라옵니다.







Comments ()