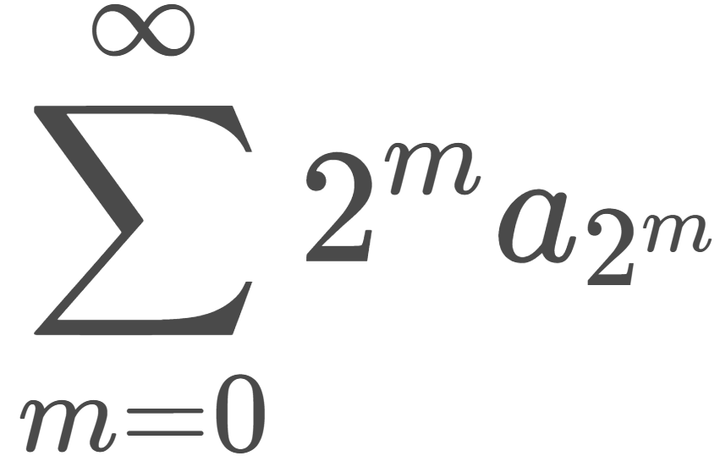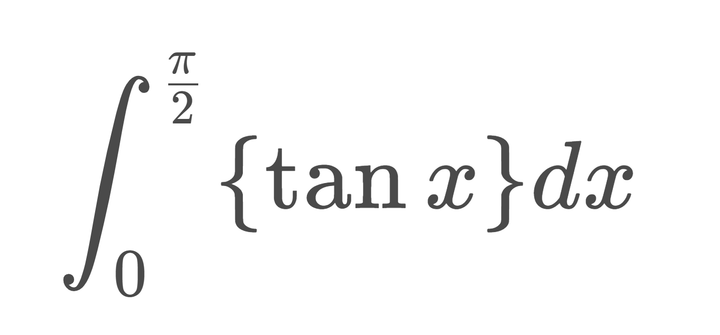
시리즈 | FA - 7. 급수의 다양한 수렴과 Fejér's Theorem
오늘은 수렴의 정의에 대한 고찰과 Elias M. Stein과 Rami Sakarchi의 [STEIN 푸리에 해석학] 에서 소개된 페예르의 정리를 살펴봅니다.
푸리에 해석 7
급수의 다양한 수렴과 Fejér's theorem
일단 다음 수식을 감상해봅시다.
$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6}$$
무한의