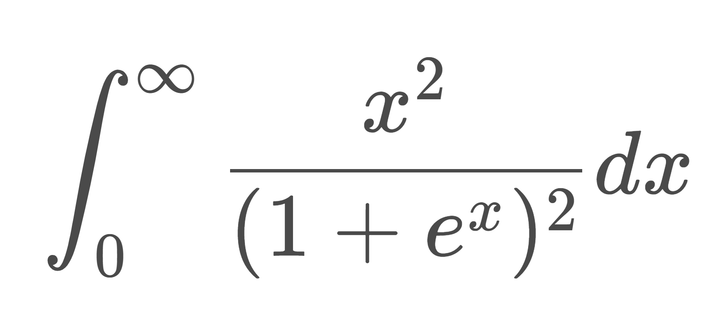오늘의 적분2 연습 문제 Solution
\[ I = \int_{0}^{\infty} \frac{\ln (1+x^2)}{x^2} dx \]
분모를 없에기 위해 \( I(a) = \displaystyle \int_{0}^{\infty} \frac{\ln (1+ax^2)}{x^2} dx \,\,\, \) 라 하자.
\[ I'(a) = \int_{0}^{\infty} \frac{1}{x^2} \frac{x^2}{(1+ax^2)} dx = \int_{0}