테브난 정리 | Thevenin's Theorem

전자기학 시간에 여러 문제를 풀다보면 회로의 각 부분에 흐르는 전류를 구하는 문제를 풀 때가 있다. 그러나, 회로는 회로대로 꼬여 있고, 문제에서 키르히호프 법칙을 쓰면 식이 너무 복잡해져서 힘든 경우가 많다.

그러나, 이런 복잡한 회로도 단 2개의 장치로 단순화할 수 있다고 하면 믿기겠는가? 이 글에서는 이러한 복잡한 회로도 단 하나의 저항과 하나의 전압원으로 나타낼 수 있는 테브난 정리에 관해서 설명하고자 한다.

테브난 정리와 테브난 등가회로

테브난 정리란 임의의 선형 2단자 회로망은 한 부분을 하나의 테브난 저항과 테브난 전압원이 연결된 테브난 등가회로로 표현할 수 있다는 정리다. 다시 말해, 밑의 그림처럼 2개의 전선을 통해 부분 A, B로 분리된 회로에서 두 부분 중 부분 A를 저항 1개, 전압원 1개로 연결된 회로로 단순화할 수 있다는 말이다.

위 그림에서 $V_T$를 테브난 등가 전압, $R_T$를 테브난 등가 저항이라고 한다.

부분 B의 관점에서, 부분 A 대신에 테브난 등가회로를 연결하여도 걸리는 전압이나 흐르는 전류가 동일하다. 따라서, 부분 B가 보기에는 부분 A나 테브난 등가 회로나 같다는 말이다.

테브난 등가회로를 구하는 방법

이제, 테브난 정리를 활용하여 회로를 단순화하는 방법에 대해서 알아보자. 테브난 등가회로를 구하기 위해서는 테브난 등가 전압 $V_T$, 테브난 등가 저항 $R_T$를 구해주면 된다.

테브난 등가 전압 구하기

테브난 등가 전압은 등가 회로를 구하는 부분에서 측정되는 개방 회로 전압으로 구할 수 있다. 이를 계산하기 위해서는, 테브난 등가 저항을 구하고자 하는 부분(위 그림에서의 부분 A)의 단자를 개방한 이후, 두 단자 사이의 전위차를 구해야 한다.

예시를 통해 테브난 등가 전압을 구하는 방법을 익혀 보자. 아래 회로의 테브난 등가 전압을 구하는 과정은 다음과 같다.

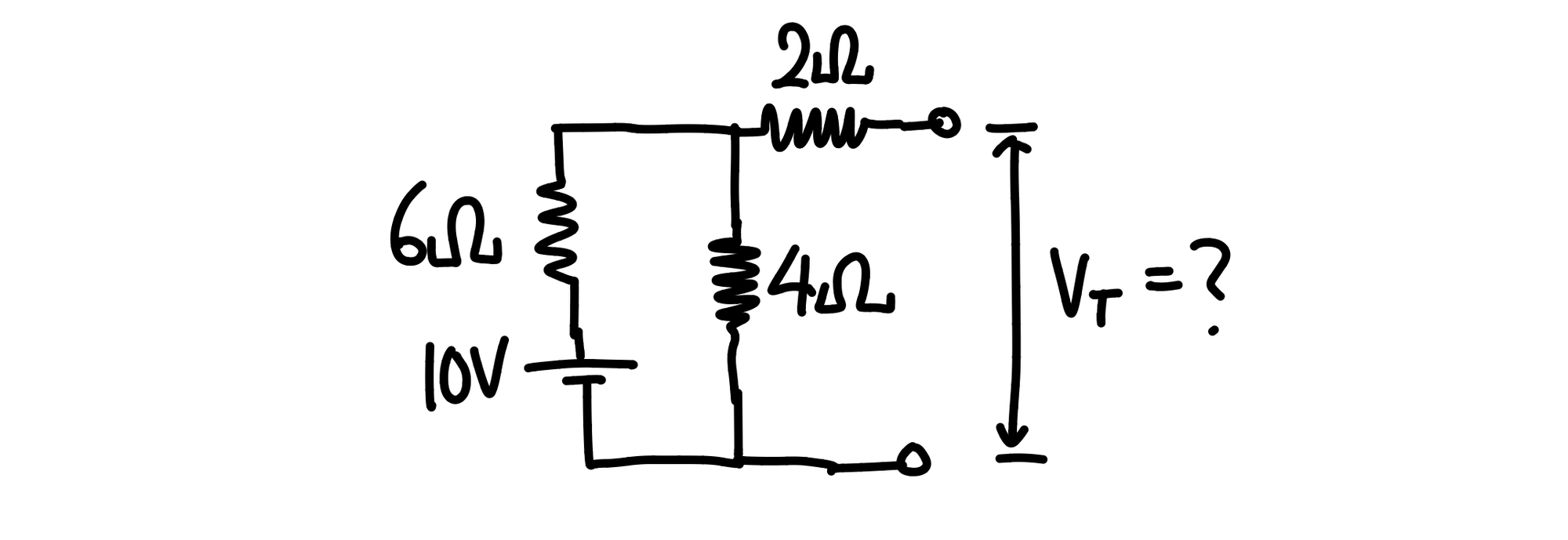
여기서 전압을 구하고자 하는 두 부분이 단락되었으므로, 2Ω 저항에 흐르는 전류는 0이다. 따라서, 회로를 다시 표현하면, 4Ω 저항 양단에 걸리는 전압차가 테브난 등가전압이다. 저항의 직렬 연결 상황에서 전압 분배를 생각해보면, 테브난 등가 전압은 다음과 같이 구할 수 있다.

$$V_T = 10 \times \frac{4}{6+4} = 4(\rm{V})$$

테브난 등가 저항 구하기

테브난 등가 저항은 회로 내의 모든 독립 전원을 제거한 뒤 등가 회로가 연결된 부분에서 보았을 때의 회로의 저항을 계산하여 구할 수 있다. 이 과정에서 독립 전압원의 경우에는 전압원의 전압을 0V로 설정하기 위하여 회로상의 그 부분을 단락(연결)하고, 독립 전류원의 경우에는 전류원의 전류를 0A로 설정하기 위하여 회로상의 그 부분을 개방하면(끊으면) 된다.

위에 들었던 예시의 테브난 등가 저항을 구해 보자. 이 경우 10V 전지를 단락하면 6Ω과 4Ω 저항이 병렬 연결된 저항에 2Ω 저항이 직렬연결된 저항의 등가 저항을 계산해 주면 된다.

$$R_T = 6 // 4 + 2 = \frac{6 \times 4 }{6 + 4} + 2=4.4(Ω)$$

따라서, 위 예시의 테브난 등가회로를 구한 결과는 다음과 같다.

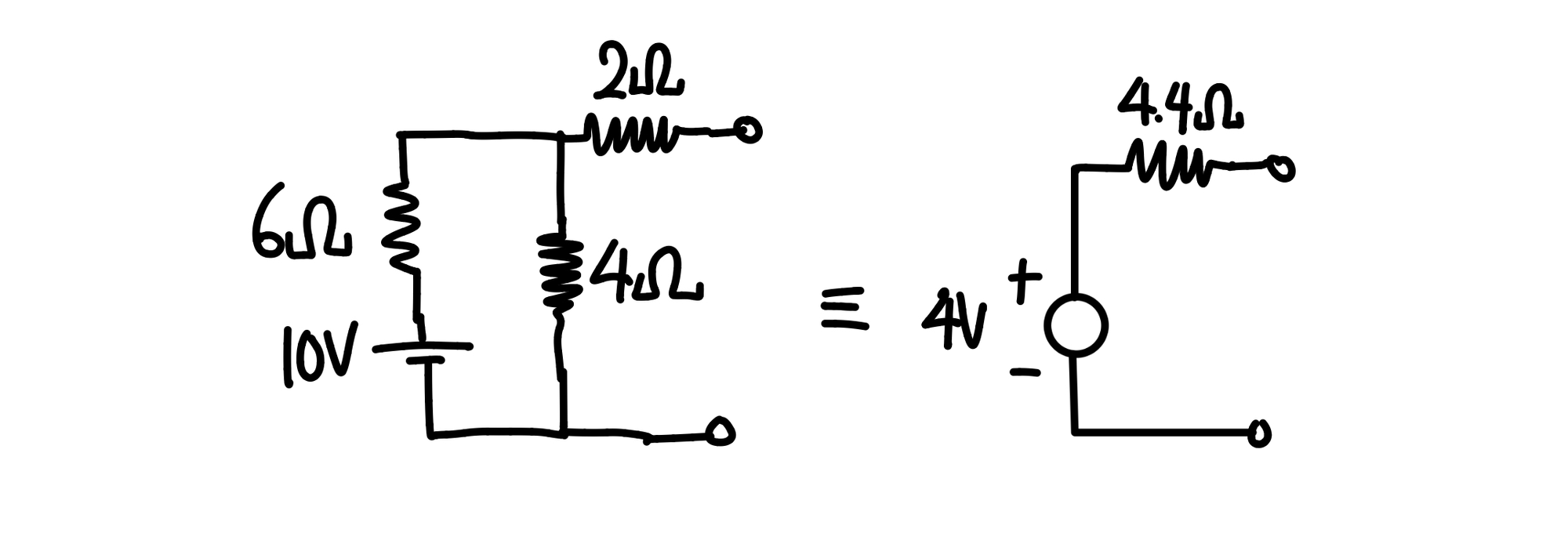
테브난 정리의 활용 : RLC 회로 해석

테브난 정리를 활용하면 복잡한 RLC 회로를 간단화해서 회로를 더 쉽게 분석할 수 있다. 다음 예제를 통해 테브난 정리를 RLC 회로 분석에 활용하는 예시를 살펴보자.

다음 회로에서 스위치를 닫은 후 지난 시간을 t라고 했을 때, 인덕터에 흐르는 전류를 t에 관해 표현해보자.

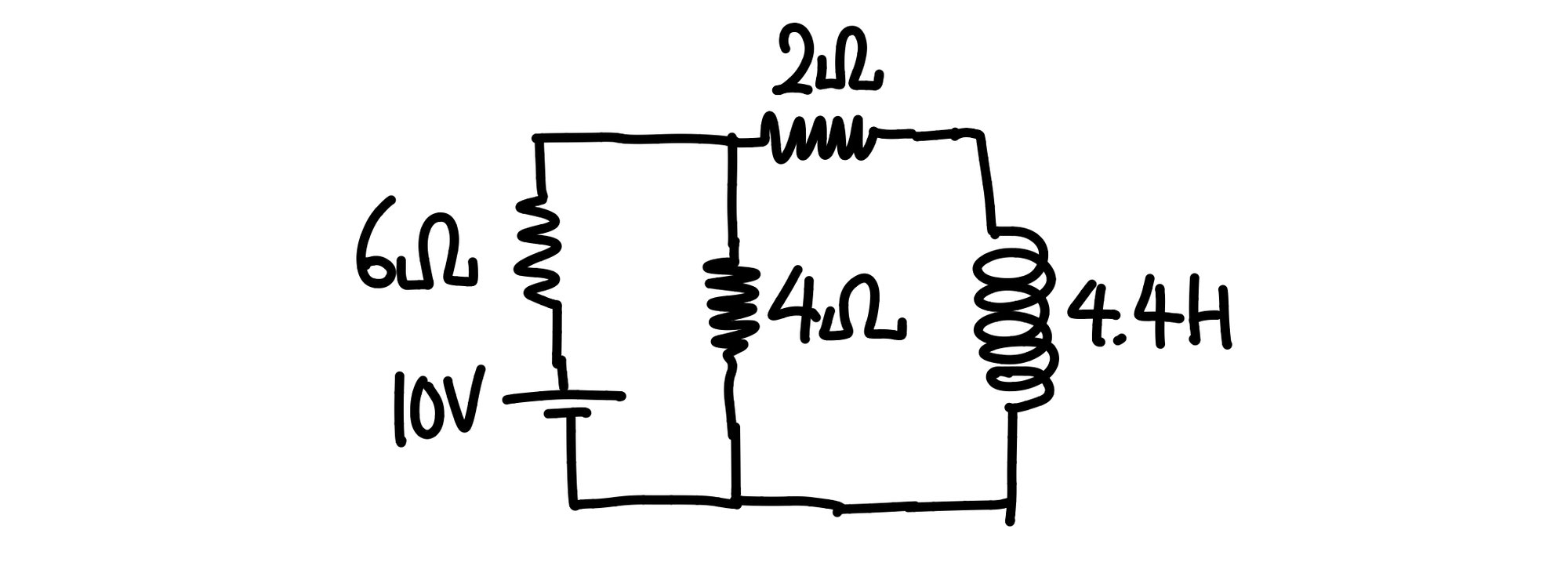
딱 문제를 마주했을 때는 저항과 인덕터가 복잡하게 연결되어 있어서 전류를 어떻게 잡야아 할 지 감이 안 온다. 이 때, 테브난 정리를 활용하여 인덕터 이외의 부분을 모두 다음과 같이 테브난 등가회로로 변환할 수 있다.

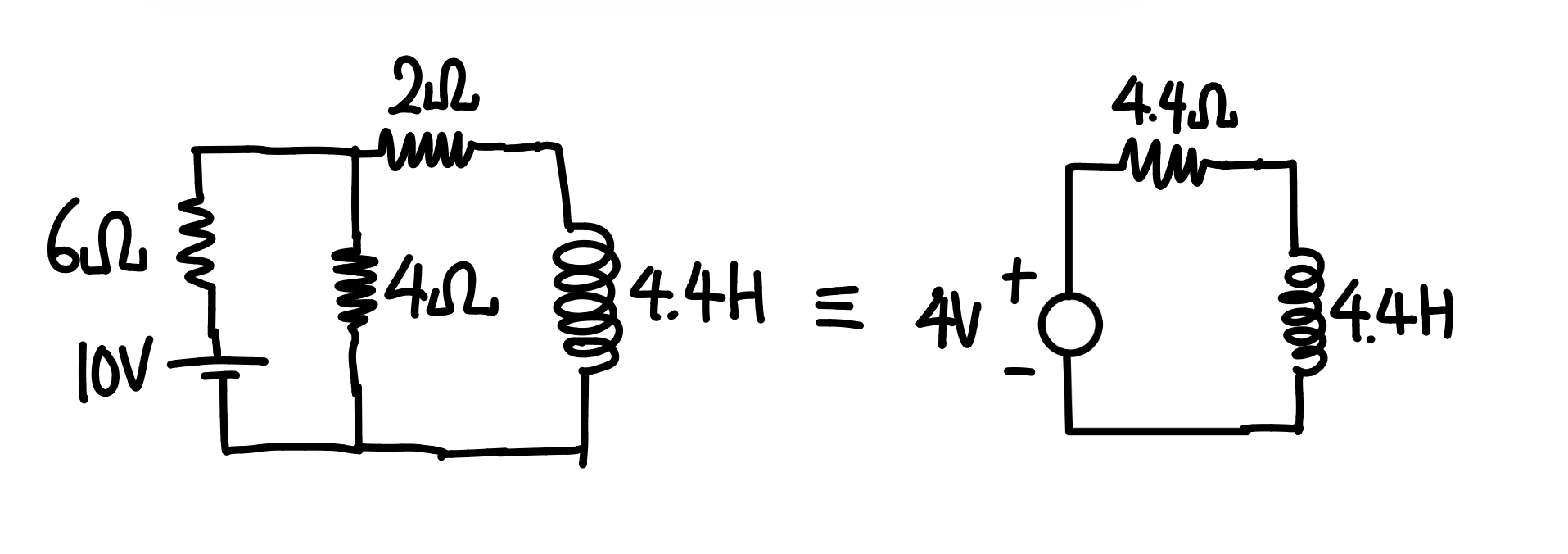
오! 문제가 많이 간단해졌다. 전형적인 RL 문제 해결 방법으로 마저 풀어보자.

테브난 등가회로가 적용된 회로에 KVL(키르히호프 전압 법칙)을 적용하면 다음과 같다.

$$ V - Ri - L \frac{di}{dt} = 0$$

$$ 4 - 4.4 i - 4.4 \frac{di}{dt} = 0$$

여기서 시상수 $\tau = 1(\rm{s})$이므로, 미분방정식을 풀면 다음과 같다.

$$ i(t) = \frac{4}{4.4} ( 1 - e^{-t})$$

결론

테브난 정리는 복잡한 선형 회로망을 해석하는 과정을 획기적으로 단순화하는 강력한 도구이다. 앞으로 복잡한 회로를 마주한다면 놀라지 말고 더 간단하게 풀 수 있는 방법을 찾아보는 마음가짐을 가져 보자.

참고 자료

https://www.youtube.com/watch?v=oD91Ohq2rEg&list=PL9KyzjPFbwH37w22z-UHVEt37pdJHjZ7x&index=10&pp=iAQB