자연수의 역수들의 합 얘기

이 글에선 자연수의 역수들의 합에 대한 이런저런 얘기를 합니다.
$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+ \frac{1}{4}+\frac{1}{5}+\cdots$$
(조화급수)
조화급수의 부분합을 조화수라고 부르고 이는 다음과 같습니다.
$$H_N=\sum_{n=1}^{N}\frac{1}{n}$$
조화급수는 해석학에서 다루는 급수이론의 근간을 이루는 급수로서 발산함이 잘 알려져 있습니다.
발산함을 최초로 증명한 것으로 알려진 건 Nicole Oresme로 1350년대 쯤에 아래와 같이 조화급수의 발산을 증명했다고 합니다.
증명의 아이디어는 $\, \, (2^k < n\leq 2^{k+1})$인 \(n\)을 \(2^{k+1}\)로 근사하는 것 입니다. 그러면 각 k에 대해 $1/2^{k+1}$이 $2^{k+1}-2^k=2^k$ 개 이니 뭉텅이를 $1/2$로 근사할 수 있습니다.
$$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\cdots$$
$$\geq 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}+\frac{8}{8}+\frac{1}{16}+\cdots$$
$$\Rightarrow \, \, \, \, \sum_{n=1}^{2^m}\frac{1}{n}=1+\sum_{k=0}^{m}\sum_{n=2^k+1}^{2^{k+1}}\frac{1}{n}$$
$$\geq 1+\sum_{k=0}^{m}\sum_{n=2^k+1}^{2^{k+1}}\frac{1}{2^{k+1}}$$
$$\geq 1+\sum_{k=0}^{m}\frac{1}{2} = 1+\frac{m}{2}$$
따라서 m이 무한대로 감에 따라 조화급수의 하계가 발산하니 조화급수도 발산함을 알 수 있습니다.
이 아이디어를 일반화 한 것이 Cauchy Condensation Test 입니다.
또한 Integral Test를 통해 조화급수가 발산함을 보일 수도 있습니다.
충분히 큰 N에 대해
$a_n=f(n)$ 이고 $f$가 단조감소이면서 연속이면
$\sum_{n=N}^{\infty}a_n$과 $\int_{N}^{\infty}f(x)dx$의 수렴/발산 여부가 같다.
$N=1$이면
$$\int_1^\infty\frac{1}{x}dx=\lim_{x\to \infty}\ln x \to \infty$$
여서 발산합니다.
Integral Test에서 하는 것은 적분으로 합을 근사하는 것입니다.
적분으로의 근사하는 방법으로 더 정량적이게 조화급수를 다룰 수 있습니다.
결과적으로는 $H_N$을 $\log$
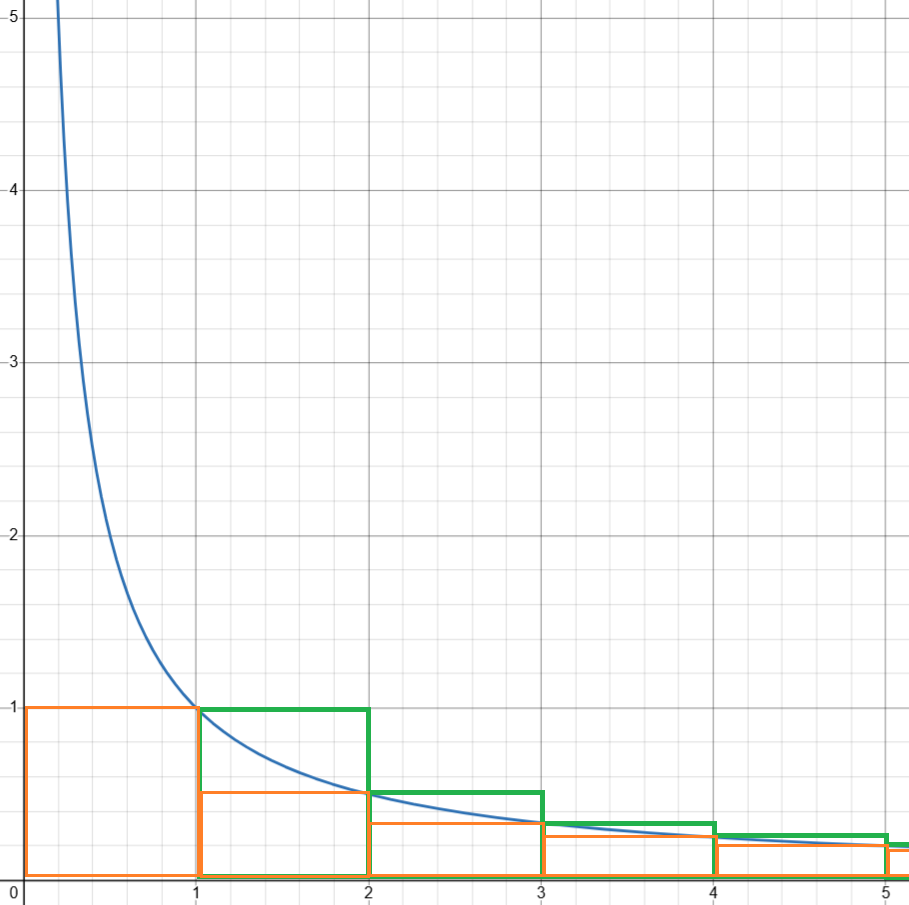
위 그림을 통해서 다음 두 부등식이 성립함을 알 수 있습니다.
(이 글에서 쓰는 log는 자연로그 입니다)
$$\log (N+1)=\int_1^{N+1}\frac{1}{x}dx < \sum_{n=1}^{N}\frac{1}{n}$$
$$ \sum_{n=1}^{N}\frac{1}{n} < 1 + \int_1^N\frac{1}{x}dx = 1+\log N$$
$$\Rightarrow \log (N+1)<H_N<1+\log N$$
따라서 $H_N$이 $\log N$ 정도로 발산합니다. 또한
$$s_N=H_N-\log N$$
으로 두면
$$s_{N+1}-s_N=\frac{1}{N+1}-(\log (N+1)-\log N)=\frac{1}{N+1}-\int_{N}^{N+1}\frac{1}{x}dx<0$$
이어서 $s_N$이 감소수열임을 알 수 있고, 위 부등식을 이용해서
$$0<\log(1+\frac{1}{n})<H_N-\log N =s_N$$
이니, 단조수렴정리로 $s_N$이 극한값을 가지는데, 이 극한값으로 정의되는 수가
오일러-마스케로니 상수이고, $\gamma$로 표기합니다
$$\lim_{N\to \infty}(H_N-\log N)=\gamma \approx 0.57721566\cdots$$
즉, $N$이 커짐에 따라 $\log N+\gamma$가 $H_N$으로 수렴합니다.
수렴하는 속도를 구해봅시다
$$\gamma_N=H_N-\log N=\sum_{n=1}^N \left( \frac{1}{n}-\int_n^{n+1}\frac{1}{x}dx \right)-\int_N^{N+1}\frac{1}{x}dx$$
( $\log(N+1)$로 근사하는 게 그래프로 그려봤을 때 깔끔하게 로그와 조화수의 차이가 보여서 더 자연스럽습니다. 저 뒤에 있는 적분항도 $\log(N+1)$로 근사했으면 없어져서 더 깔끔했겠지만, $\log(N+1)$보다 $\log N$이 더 간결하고 사실 큰 N에 대해서는 차이가 없는 거나 다름 없으니까 $\log N$으로 많이들 하는 것 같습니다.)
$$\lim_{N \to \infty}\gamma_N=\sum_{n=1}^{\infty} \left( \frac{1}{n}-\int_n^{n+1}\frac{1}{x}dx \right)=\gamma$$
이어서
$$\gamma-\gamma_N=\sum_{n=N+1}^{\infty} \left( \frac{1}{n}-\int_n^{n+1}\frac{1}{x}dx \right)+\int_N^{N+1}\frac{1}{x}dx $$
$$ 0< \frac{1}{n}-\int_n^{n+1}\frac{1}{x}dx <\frac{1}{n}-\frac{1}{n+1}<\frac{1}{n^2}$$
$$\therefore 0< \sum_{n=N+1}^{\infty} \left( \frac{1}{n}-\int_n^{n+1}\frac{1}{x}dx \right) < \sum_{n=N+1}^{\infty}\frac{1}{n^2}<\int_N^\infty\frac{1}{x^2}dx=\frac{1}{N}$$
그래서
$$0\leq \gamma-\gamma_N<\frac{1}{N}+\log(1+\frac{1}{N})<\frac{1}{N}+\frac{1}{N}=\frac{2}{N} $$
정도로 오차 바운드를 잡을 수 있습니다.
$\gamma_N=H_N-\log N$을 넣으면
$$H_N\leq \log N+\gamma<H_N+\frac{2}{N}$$
$$\log N+\gamma-\frac{2}{N}<H_N\leq\log N+\gamma$$
숫자를 넣어보면
$H_{1000}$은 $\log (1000)+\gamma$보다 0.002보다 차이가 적게 작게 됩니다 .
이를 이용해 $O$ notation으로 다음과 같이 나타낼 수도 있겠습니다.
$$H_N=\log N + \gamma +O\left(\frac{1}{N}\right)$$
여기서 더 정교하게 오차를 알고 싶으면 오일러-메클로린 합공식으로 조화수를 계산해서 전개하면 된다고 합니다.
또한 재밌는 점은 이 로그로 근사한 것을 기반으로 보면
$$H_{2^m}=\log 2^m+\gamma+O\left(\frac{1}{2^m}\right)\approx (0.6931)m+(0.5772)$$
으로 아까 아주 기초적인 방법으로 하계를 잡았던 것이 스케일도 같고, 상수도 비슷한 굉장히 잘 잡힌 근사였습니다!
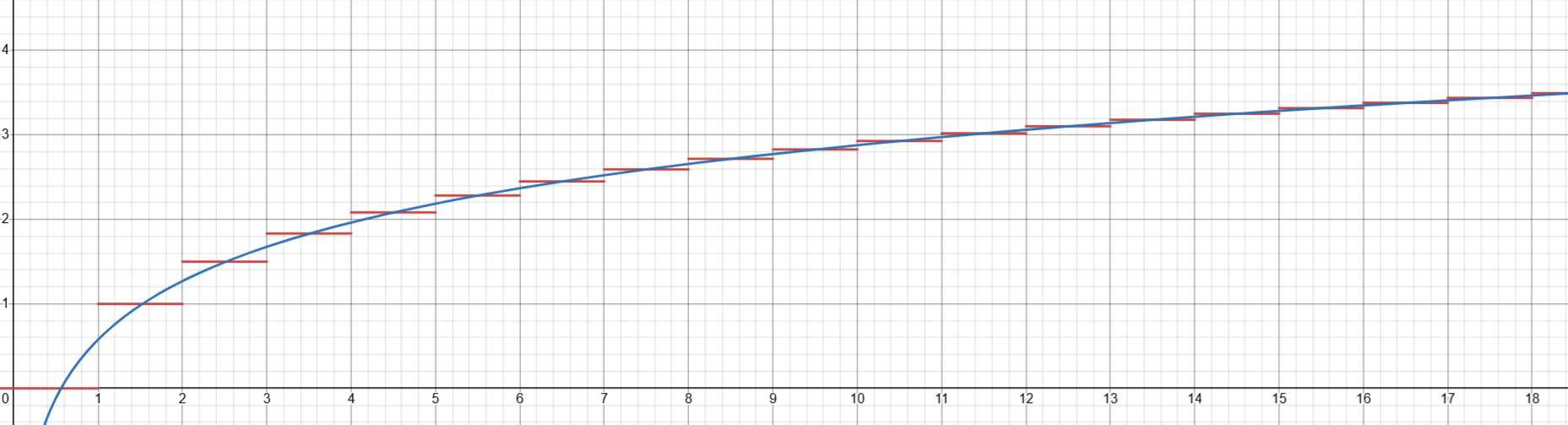
조화급수의 발산속도(정확히는 조화급수의 부분합의 발산속도)를 생각해보면 정말 더럽게 느리게 발산합니다.
저 급수를 처음 봤을 때가 기억이 납니다. 합이 유한하지 않을까 라고 생각했는데... 끝없이 작아지는 값들을 더해서 수렴하지 않는다는 게 처음 보는 뇌에겐 굉장히 비직관적입니다. 어떻게 보면 이 급수에 대한 이해가 수학에서 정의되는 무한대에 대한 올바른 직관을 머리에 익히게 되는데에 중추적인 급수인 것 같습니다.
조화급수를 머리에서 이리저리 굴리다 보면 저 급수에서 항을 얼마나 빼야 수렴하게 될지에 대한 의문점이 듭니다. 저렇게 느리게 발산하는 만큼 항을 그렇게 많이 안 빼도 수렴하지 않을까? 라는 생각을 먼저 하게 되는 것 같습니다.
자연수에서 아주 얇게 분포되는 소수들의 역수의 합의 거동은 어떨까요?
이 질문에 대한 대답은 오일러가 그 유명한 제타함수와 오일러 곱 공식을 최초로 고안해서 하게 됩니다.
놀랍게도, 소수의 역수들의 합은 발산합니다!
$$\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\frac{1}{17}+\cdots\to \infty$$
$\sum_p,\prod_p$는 모든 소수에 대한 합, 곱입니다.
$$\zeta (s) =\sum_{n=1}^\infty\frac{1}{n^s}=\prod_p\frac{1}{1-p^{-s}}$$
오일러 곱공식이 제타함수가 소수와 연관 돼 있는 이유입니다.
"It is important to remark that this identity is an analytic expression of the fundamental theorem of arithmetic."
[스타인 푸리에 해석] 에서는 이를 산술의 기본 정리의 해석적 표현이라고 합니다.
증명은 공식에서 유한곱과 유한합으로 둔 후 부등식을 잡아서 무한합과 무한곱으로 바꾸면 됩니다.
이 공식을 이해해 보자면,
$$\frac{1}{1-r}=1+r+r^2+r^3+\cdots \, \, \, (|r|<1)$$
이므로
$$\prod_p\frac{1}{1-p^{-s}}=\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots\right)\left(1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\cdots\right)\left(1+\frac{1}{5}+\frac{1}{5^2}+\frac{1}{5^3}+\cdots\right)\cdots$$
이항정리를 증명할 때처럼 생각해서 합들의 곱을 각 합 뭉텅이에서 항을 하나씩 골라서 다 곱한 후 더하는 것을 모든 고르는 경우에 대해 하는 것으로 생각하면,
$1/n^s$이 산술의 기본정리에 의해서 $1/2^{e_1s},1/3^{e_2s},1/5^{e_3s},\cdots,1/p_n^{e_ns},\cdots$ 들의 곱으로 분해가 돼서 결국 좌변의 모든 항들과 우변의 합 뭉텅이에서 하나씩 골라서 만든 항들이 1-1로 대응이 되면서 같아진다는 것을 알 수 있습니다.
오일러 곱공식과 로그함수의 근사로 소수 역수 합의 발산을 쉽게 알 수 있습니다.
$0<x<1/2$이면
$$\log(\frac{1}{1-x})=x+\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}\cdots$$
$x^3$부터 분모에 오는 수들을 2로 바꿔서 더 커지게 하고, $x$들을 빼냅니다.
$$<x+\frac{x^2}{2}+x\frac{x^2}{2}+x^2\frac{x^2}{2}\cdots$$
빼낸 $x$에 $x<1/2$를 적용합니다
$$<x+\frac{x^2}{2}+\frac{x^2}{4}+\frac{x^2}{8}+\cdots=x+x^2$$
따라서 이를 사용해서
$$\sum_{p\leq n}\frac{1}{p}+\frac{1}{p^2}>\sum_{p\leq n}\log\left(\frac{1}{1-\frac{1}{p}}\right)$$
$$=\log\left(\prod_{p\leq n}\frac{1}{1-\frac{1}{p}}\right)$$
$$=\log\left(\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots\right)\left(1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\cdots\right)\cdots\left(1+\frac{1}{p_M}+\frac{1}{p_M^2}+\frac{1}{p_M^3}+\cdots\right)\right)$$
$n$이하인 최대의 소수 $p_M$까지의 소수들의 역수 급수 뭉텅이로 만들어지는 곱은$n$이하의 모든 자연수의 역수를 만들어냅니다.
왜냐하면 $n$이하 자연수 중에서 소수이면 당연히 포함이 되고, 합성수이면 인수분해를 했을 때 그 수를 구성하는 소수들은 당연히 그 수를 넘을 수 없고, 따라서 $n$보다 작은 소수들이어서 $p_M$까지의 소수들의 역수 급수 뭉텅이로 만들어질 수 있습니다.
$$>\log\left(\sum_{k=1}^{n}\frac{1}{k}\right)$$
$$>\log\log n$$
$$\therefore \log\log n<\sum_{p\leq n}\frac{1}{p}+\frac{1}{p^2}<\sum_{p\leq n}\frac{1}{p}+1$$
$$\sum_{p\leq n}\frac{1}{p}> \log\log n -1$$
따라서 $n\to \infty$임에 따라 소수 역수의 합이 발산합니다.
부등식들을 O notation으로 손을 보고 더 정교하게 논증하면
$$\lim_{n \to \infty}\left(\sum_{p\leq n}\frac{1}{p}-\log\log n\right)=M$$
$M\approx 0.26149721\cdots$으로 차이가 수렴하고, 이를 마이셀-멀텐스 상수라 부른다고 합니다.
소수의 역수의 합도 발산한다니 생각해보면 참 놀라운 결과입니다. 소수 리스트를 보면 큰 수들에 대해서는 소수간 간격들이 엄청 넓어지는데 불구하고 발산한다는 것입니다!
하지만 이 $\log \log n$의 결과도 완전히 쌩뚱맞지는 않고, 해석할 여지가 있습니다. 소수 역수의 합이 조화급수를 띄엄띄엄 확률적으로 더한 거라고 생각해 봤을 때 저 $\log \log n$의 발산속도라는 결과를 직관적으로 어느 정도 예측할 수 있습니다.
예를 들어서 조화급수에서 랜덤하게 항 몇개를 빼고 더해보는 상황을 생각해 봅시다. 각 항이 있을 확률을 1/2로 하고 발산속도를 계산해보면 평균적으로 대략 조화급수의 반 정도가 나올 것입니다.
소수 또한 분포가 랜덤하다고 볼 수 있습니다.
따라서 원래의 조화급수는 다음과 같이 적분으로 근사하던 것을
$$\sum\frac{1}{n}\approx \int\frac{1}{x}dx=\log x + C$$
소수의 밀도가 N에서 $\frac{1}{\log N}$, 즉 숫자 N을 뽑았을 때 그 수가 소수일 확률이 $\frac{1}{\log N}$이니,
따라서 저 각 숫자에 소수일 확률을 부여해주는 함수를 곱해서 적분하면
$$\sum \frac{1}{p} \approx \int \frac{1}{x \log x}dx =\log\log x +C$$
이게 돼서 저 $\log \log n$의 결과도 꽤 개연성이 있다고 생각할 수도 있겠습니다.
+
소수정리를 통해서
$$\pi(x) \sim \text{Li}(x)$$
임을 알 수 있는데,
$$\text{Li}(x)=\int_2^x\frac{1}{\log x}dx$$
여서 $\frac{1}{\log x}$을 소수의 밀도 또는 소수일 확률로 생각해서 저 확률을 $x$까지 적분해서 $x$보다 작은 소수의 개수인 $\pi(x)$가 나온다고 생각할 수 있습니다.
그러면 도대체 얼마나 조화급수에서 항들을 제거해야지 수렴을 할지 의문이 드는데,
바로 위에서 확률로 해석한 직관으로 생각하면 결국 확률함수$p(x)$
$$\int_c^\infty\frac{p(x)}{x}$$
가 수렴하면 되므로 수의 밀도가
$$\frac{1}{x^{\epsilon}} \, \, , \, \, \, \frac{1}{(\log x)^{1+\epsilon}}$$
정도의 스케일로 감소할 정도로 항들을 제거하면 될 것이라고 추측할 수 있습니다.
실제로 이런 급수의 예시로 Kempner Series가 있습니다.
이 급수에서 조화급수의 항을 제거하는 규칙은 역수인 숫자의 자릿수 중에서 9가 있으면 제거하는 것입니다.
위에서 얘기해본 확률적 생각으로 수렴판정을 예측해 보기 위해 대략적인 $p(x)$를 보자면
간단한 조합적 논증으로
1~10중에서 제거 안 되는 항의 개수는
10-1=9개
1~100중에서는
100-(일의 자리 9인 개수)-(10의 자리 9이면서 1의 자리 9 아닌 개수)
=100-10-9=81개
1~1000중에선
1000-(")-(")-(100의 자리 9이면서 1,10의 자리 9 아닌 개수)
=1000-100-90-81=729개
(그냥 각 자리수가 9빼면 가능한 게 9가지니까 9k해도 된다)
1~10k의 경우에는
9k개
따라서 대략적으로 (완전 엄밀하지 않고 오직 생각해보는 용도)
$$\int_1^{10^k}p(x)dx$$
는 제거 안 된 항들의 개수로
$$\int_1^{10^k}p(x)dx=9^k$$
여서 양 변을 k에 대해 미분하면 (여기 아래부터는 log를 상용로그로 하겠습니다)
$$\ln 10 \cdot 10^k p(10^k)=\ln9 \cdot 9^k$$
$k=\log x$로 하고 정리하면
$$p(x)=\log 9 x^{\log 9 -1}$$
$log9 \approx 0.9542$여서
$$p(x)=c x^{-0.0457}$$
으로써 $\frac{1}{x^{\epsilon}}$ 꼴 이어서 수렴할 것이라고 예상할 수 있습니다. 실제로
대략 $22.92067 \cdots$으로 수렴한다는 것을 Baillie라는 사람이 보였다고 합니다.
이 글에선 괜찮은 상한과 수렴성을 보려고 합니다.
먼저 $\delta(n)$은 $n$의 자릿수에 9가 있으면 0이고 아니면 1을 내뱉는 함수라고 합시다.
그러면 우리가 보고 싶은 극한은
$$\lim_{N\to \infty}\sum_{n=1}^{N}\frac{\delta(n)}{n}$$
입니다.
$$\sum_{n=1}^{10^m}\frac{\delta(n)}{n}=S_m$$
이라고 둡니다.
근사하는 아이디어는 위에서 1~10k 에서의 제거 안 되는 항들을 볼 때를 생각해서
일의 자리가 9인 수들은 일의 자리에서 반올림하고
십의 자리가 9이면서 일의 자리가 9가 아닌 수들은 십의 자리에서 반올림하고
$$\cdots$$
이렇게 해서 상한을 잡는 것입니다.
1~1000을 예시로 들면
$$S_3=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{1000})-(\frac{1}{9}+\frac{1}{19}+\frac{1}{29}+\cdots+\frac{1}{999})$$
$$-(\frac{1}{90}+\frac{1}{91}+\cdots+\frac{1}{98}+\frac{1}{190}+\frac{1}{191}+\cdots+\frac{1}{198}+\cdots+\frac{1}{990}+\frac{1}{991}+\cdots+\frac{1}{998})$$
$$-(\frac{1}{900}+\frac{1}{901}+\cdots+\frac{1}{988})$$
$$<(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{1000})-(\frac{1}{10}+\frac{1}{20}+\frac{1}{30}+\cdots+\frac{1}{1000})$$
$$-(\frac{1}{100}+\frac{1}{100}+\cdots+\frac{1}{100}+\frac{1}{200}+\frac{1}{200}+\cdots+\frac{1}{200}+\cdots+\frac{1}{1000}+\frac{1}{1000}+\cdots+\frac{1}{1000})$$
$$-(\frac{1}{1000}+\frac{1}{1000}+\cdots+\frac{1}{1000})$$
$$=H_{1000}-\frac{1}{10}H_{100}-\frac{9}{100}H_{10}-\frac{81}{1000}H_{1}$$
이 방식으로 하고 조화수를 로그로 근사하여
$$S_m<H_{10^m}-\sum_{k=0}^{m-1}\frac{9^{m-k-1}}{10^{m-k}}H_{10^k}$$
$$<1+\ln(10^m)-\frac{1}{9}\sum_{k=0}^{m-1}\left(\frac{9}{10}\right)^{m-k}\ln(10^k+1)$$
$$<1+m \ln 10-\frac{1}{9}\sum_{k=0}^{m-1}\left(\frac{9}{10}\right)^{m-k}k\ln 10$$
pf)
$$\sum_{k=0}^{n-1}\left(\frac{9}{10}\right)^{n-k}k=\sum_{j=1}^{n}(n-j)\left(\frac{9}{10}\right)^{j}$$
$$=n\sum_{j=1}^{n}\left(\frac{9}{10}\right)^{j}-\sum_{j=1}^{n}j\left(\frac{9}{10}\right)^{j}$$
첫 번째 항은 등비수열이고, 두 번째 항은 등비수열 꼴의 다항식을 미분한 후 x를 곱하면 나오는 형태이므로 시그마 없는 닫힌 형태로 나오게 되고, 후는 계산 열심히ㅜ
$$=1+m \ln 10-\frac{1}{9}\sum_{k=0}^{m-1}\left(\frac{9}{10}\right)^{m-k}k\ln 10$$
$$=1+m \ln 10-10\ln 10\left(\frac{9}{10}\right)^{m}-m\ln 10 +10 \ln 10$$
$$=1+10\ln 10\left(1-\left(\frac{9}{10}\right)^{m}\right)$$
따라서
$$S_m<1+10\ln 10\left(1-\left(\frac{9}{10}\right)^{m}\right)<1+10\ln 10$$
이므로 단조수렴정리로 수렴함을 알 수 있고, 극한값의 상계가 $1+10\ln 10$임을 알 수 있습니다.
$1+10\ln 10\approx 24.02585\cdots$로 꽤나 투박하게 했는데도 실제 값인 $22.92067 \cdots$와 크게 다르지 않습니다!
마지막으로 조화급수에 대해 Mathologer이라는 채널에서 다룬 영상이 있는데 너무 내용도 좋고 이 채널 자체도 너무 좋아서 시간 될 때 보시는 걸 추천드립니다.

끝!



Comments ()