시리즈 | Integration - 오늘의 적분 1

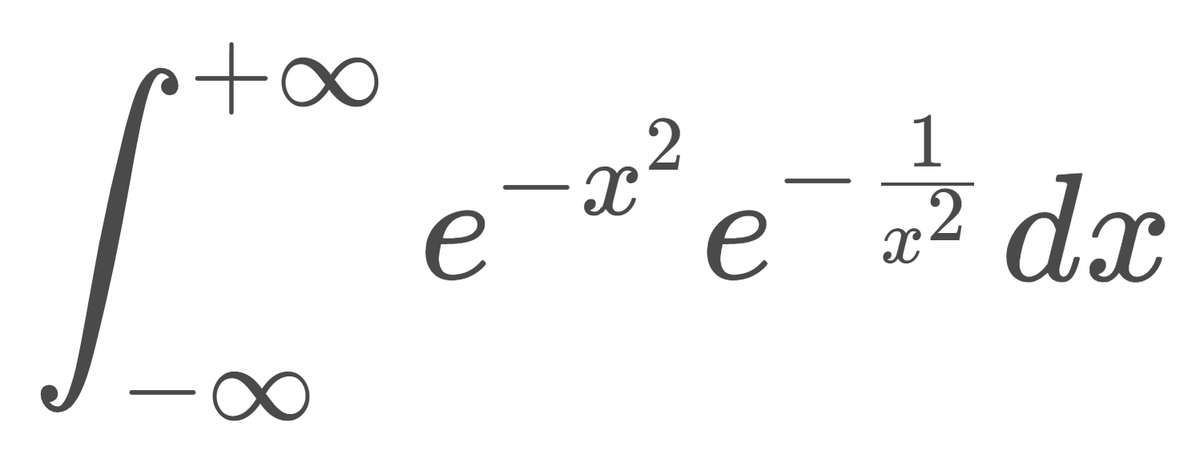
댓글로 적분 추천

오늘의 적분이라는 이름을 달고도 매일 글이 올라오지 않는다.

처음에는 쉬운 문제로 시작해 더 어렵고 복잡한 문제들은 나중에 다루어 보자

ㅤ

ㅤ

정석적인 가우스 적분

\[ \int_{- \infty}^{+ \infty} e^{-x^2} dx = \sqrt \pi \]

의 변형인

\[ I = \int_{- \infty}^{+ \infty} e^{-x^2} e^{- \frac{1}{x^2}} dx \]

을 풀어보자.

아이디어와 이론, 기교도 쉽고 일반적으로 많이 사용되니 한번 시도해보면 좋을 것이다.

ㅤ

ㅤ

ㅤ

ㅤ

ㅤ

(풀이)

ㅤ

\[ I = 2 \int_{0}^{ \infty} e^{-(x^2 + \frac{1}{x^2})} dx \]

일단 피적분 함수는 \( x \to \frac{1}{x} \) 의 치환에 대해 대칭이다. 해당 치환을 적분에 적용한다고 생각하면 \( dx \to - \frac{1}{x^2} dx \) 로 변환된다. \( dx = 1 dx \) 로 보고 위끝과 아래끝이 바뀌니 부호가 한번 바뀐다.

\[ I = 2 \int_{0}^{ \infty} e^{-(x^2 + \frac{1}{x^2})} (1) dx = 2 \int_{0}^{ \infty} e^{-(x^2 + \frac{1}{x^2})} ( \frac{1}{x^2} ) dx \]

의 두 식을 더하면,

\[ I = \int_{0}^{ \infty} e^{-(x^2 + \frac{1}{x^2})} \left( 1 + \frac{1}{x^2} \right) dx \]

이 상태까지 식 변형을 성공했다면 문제가 끝난 것이나 다름없다.

\[ \frac{d}{dx} \left( x-\frac{1}{x} \right) = 1 + \frac{1}{x^2} \]

\[ \left( x-\frac{1}{x} \right)^2 +2 = x^2 + \frac{1}{x^2} \]

이므로

\[ \left( x-\frac{1}{x} \right) = t \,\,\, : \,\,\, \left( 1 + \frac{1}{x^2} \right) dx = dt \]

의 치환이 가능하다.

\[ I = \int_{-\infty }^{ \infty} e^{-(t^2 + 2) } dt = e^{-2} \int_{-\infty }^{ \infty} e^{-t^2 } dt = \frac{ \sqrt{ \pi}}{e^2} \]

ㅤ

\[ I = \frac{ \sqrt{ \pi}}{e^2} \]