시리즈 | Integration - 오늘의 적분 3
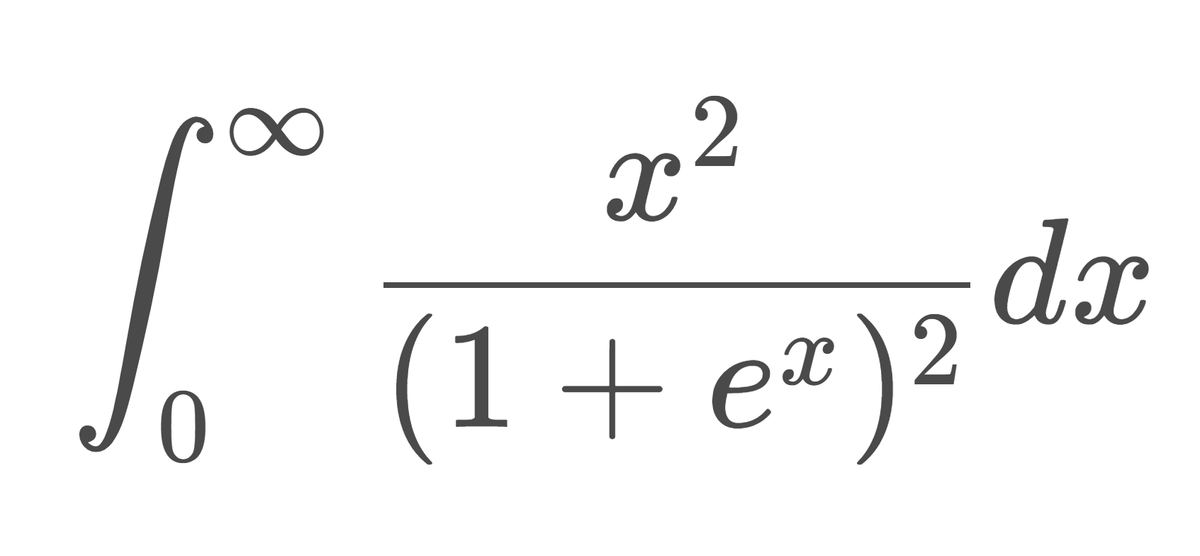
오늘은 조금은 클래식하고 간단한 지수 적분을 살펴본다.
\[ I = \int_{0}^{\infty} \frac{x^2}{(1 + e^x)^2} dx \]
ㅤ
ㅤ
ㅤ
ㅤ
일단 가장 먼저 생각할 수 있는 것은 \( e^x \) 를 곱한 뒤 치환하는 것인데 그 방법은 \(x^2\) 이 \( \ln^2 x \) 가 되어 분자와 겹치며 적분하기 불편해진다.
그러니
의 철칙을 따라보자.
ㅤ
등비급수는 간단하게 \(|r|<1\) 인 경우에 한해 수렴시킬 수 있다. 물리에서도 가끔 사용한다 들었다.
\[ \sum_{n=0}^{\infty} r^n = \frac{1}{1-r} \]
\( r\to -r \) 의 치환으로
\[ \sum_{n=0}^{\infty} (-1)^n r^n = \frac{1}{1+r} \]
ㅤ
그러나 적분 구간인 \( (0, \, \infty ) \) 에서는 \( r \)이 되어야 할 \( e^x \) 가 범위 내에 있지 않다. 그러니 \( e^x \to e^{-x} \) 로 바꾸어 주어야 한다. \( e^{2x} \) 를 빼내자는 것이다.
\[ I = \int_{0}^{\infty} \frac{x^2}{e^{2x}(1 + e^{-x})^2} dx = \int_{0}^{\infty} \frac{x^2 e^{-2x}}{(1 + e^{-x})^2} dx \]
일단 \( r = e^{-x} \) 를 대입한다면 양수 \( x \) 에 대하여
\[ \sum_{n=0}^{\infty} (-1)^n e^{-nx} = \frac{1}{1+e^{-x}} \]
이므로 분모를 제곱으로 만들기 위해서는 양변을 \( x\)에 대하여 미분하면 될 것이다. 그럼 \( n=0 \) 인 항은 사라지니
\[ - \sum_{n=0}^{\infty} (-1)^n n e^{-nx} = \frac{e^{-x}}{( 1+e^{-x})^2} = \sum_{n=1}^{\infty} (-1)^{n+1} n e^{-nx}\]
ㅤ
이걸 바로 적분식에 대입한다.
\[ I = \int_{0}^{\infty} x^2 e^{-x} \left( \sum_{n=1}^{\infty} (-1)^{n+1} n e^{-nx} \right) dx \]
각 항이 수렴하는 것은 자명하므로
\[ I = \sum_{n=1}^{\infty} (-1)^{n+1} n \int_{0}^{\infty} x^2 e^{-(n+1)x} dx \]
적분은 라플라스 변환이기는 하나 그런 거 외우지 않는 현명한 사람이라면 간단한 부분 적분 꼴로 계산할 수 있다.
\[ \int_{0}^{\infty} x^2 e^{-(n+1)x} dx = \left[ -\frac{e^{-(n+1)x}}{n+1} x^2 \right|_{0}^{\infty} - \left[ \frac{e^{-(n+1)x}}{(n+1)^2} \, 2x \right|_{0}^{\infty} + \int_{0}^{\infty} \frac{e^{-(n+1)x}}{(n+1)^2} \, 2 \, dx \]
로피탈 정리에 의해 앞 극한들은 모두 0 이므로
\[ \int_{0}^{\infty} x^2 e^{-(n+1)x} dx = 2 \left[ - \frac{e^{-(n+1)x}}{(n+1)^3} \right|_{0}^{\infty} = \frac{2}{(1+n)^3} \]
ㅤ
우와
\[ I = 2 \sum_{n=1}^{\infty} \frac{(-1)^{n+1} n}{(1+n)^3} = 2 \sum_{n=2}^{\infty} \frac{(-1)^{n} (n-1) }{n^3} \]
\[ I = 2 \sum_{n=2}^{\infty} \frac{(-1)^{n} }{n^2} - 2 \sum_{n=2}^{\infty} \frac{(-1)^{n} }{n^3} \]
\( n=1 \) 의 경우 값이 같으므로
\[ I = 2 \sum_{n=1}^{\infty} \frac{(-1)^{n} }{n^2} - 2 \sum_{n=1}^{\infty} \frac{(-1)^{n} }{n^3} \]
으로 쓸 수 있다.
ㅤ
리만 제타 함수에서 파생되는 한 함수를 살펴보면
\[ \eta(s) = \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n^s} = (1- 2^{1-s}) \zeta (s) \]
증명은 쉽고 적기 귀찮으므로 넘어간다. 조금만 생각해보면 자명하다.
ㅤ
\[ I = 2( -\eta (2) +\eta(3) ) = 2( - \frac{1}{2} \zeta(2) + \frac{3}{4} \zeta(3) )\]
따라서
\[ I = \int_{0}^{\infty} \frac{x^2}{(1 + e^x)^2} dx = \frac{3}{2} \zeta(3) - \frac{\pi^2}{6} \]




Comments ()