스털링 근사: 노베이스 증명
팩토리얼은 다음과 같이 비율적으로 근사된다.
\[ n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n \]
곧,
\[ \lim_{n \to \infty} \, \frac{n!}{\sqrt{2\pi n} \left(\frac{n}{e}\right)^n} = 1\]
ㅤ
ㅤ
증명의 시작은 곱을 합으로 바꾸는 것이다. 즉 \( \ln \)을 사용한다.
\[ \ln(n!) = \sum_{k=1}^{n} \ln(k) \]
이때 우변을 보면 리만 적분의 근사식처럼 보인다.
\[ \int_{a}^{b} f(x) dx = \lim_{n \to \infty} \sum_{k=0}^{n} f(a+ \frac{b-a}{n} k) \frac{b-a}{n} \]
에서 \( f(x) = \ln(x) \)일때 구간의 분할 간격을 나타내는 \( \frac{b-a}{n} \)을 \( 1\)로 바꿔 상황에 맞도록 근사하자.
\[ \int_{a}^{n+a} \ln x dx \approx \sum_{k=0}^{n} \ln(a+ k) \]
\( a=1\) 인 상황에서 \( n+1\) 을 다시 \(n\)으로 바꾼다.
\[ \int_{1}^{n} \ln x dx \approx \sum_{k=1}^{n} \ln(k) \]
ㅤ
이 근사에서 아이디어를 얻는다.
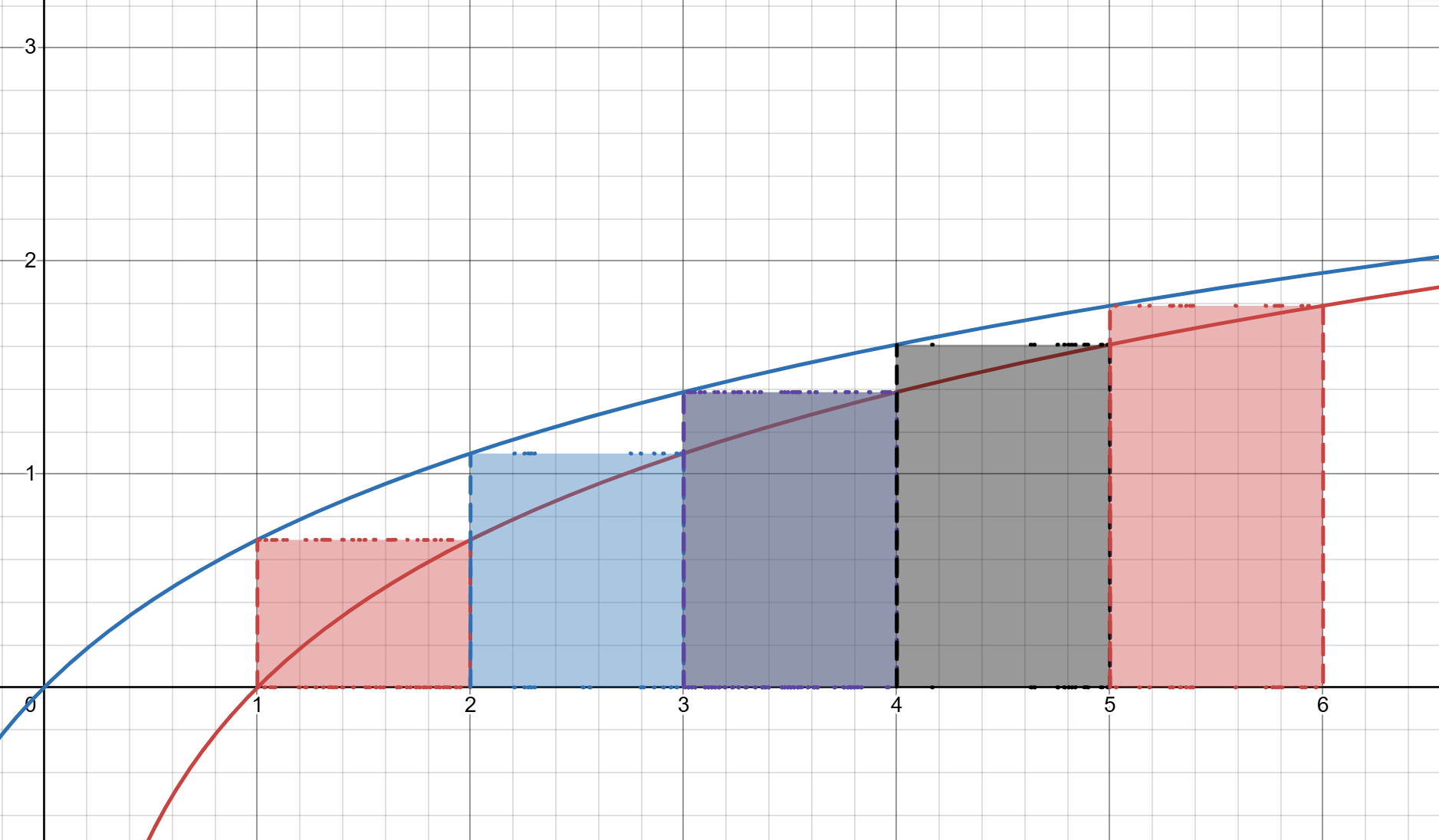
Desmos를 잘 못 써 그림이 좀 더럽다.
ㅤ
해당 근사를 바로 사용하기에는
\[ \ln n - \int_{n-1}^{n} \ln x dx \]
의 오차(위 사각형 중 빨간 곡선 위에 있는 부분)이 조금 거슬릴 수 있다.
ㅤ
이를 방지하기 위해 \( y= \ln(x+1) \)의 그래프를 활용한다.
\[ \lim_{x \to \infty} \left( \frac{d^2}{dx^2} \ln x = - \frac{1}{x^2} \right) =0\]
이므로 \( y=\ln x \)의 그래프는 결국 직선으로 근사된다.
즉, 큰 자연수 \( n\)에 대해 \( \{(x, \, y) \vert \, n \le x \le n+1 \, , \, \ln x \le y \le \ln (n+1) \} \) 의 넓이는 평행사변형으로 근사되는 \( \{(x, \, y) \vert \, n \le x \le n+1 \, , \, \ln x \le y \le \ln (x+1) \} \)의 넓이를 이등분한다고 계산한다.
ㅤ
즉, \( \ln n! \)은 \( \int_{1}^{n} \ln x \, dx \) 와 \( \int_{1}^{n} \ln (x+1) \, dx \)의 산술 평균으로 계산한다. 적분을 계산하면
\[ \ln n! \approx \left( n + \frac{1}{2} \right) \ln n -n +a \]
이때 a는 초반에 두드러지는 선형적인 오차를 나타낸다. 현재 우리는 \( \ln n! \)의 근사를 계산하고 있다. 따라서 이의 선형적인 오차는 \( n! \) 의 비율적 오차를 발생시킨다. 비율 근사를 위해서는 이를 고려해야 한다.
ㅤ
일단 식을 \( n! \) 에 대해 정리하고 보기 좋게 바꾸면 상수 c에 대해
\[ n! \approx c \sqrt{n} \left(\frac{n}{e}\right)^n \]
이다.
ㅤ
c의 값을 구하기 위해서는 팩토리얼이 들어간 비율의 극한 식을 활용하면 된다. 이 글에서는 Wallis' formula를 사용하겠다. 증명이 어마어마하게 다양하다.
\[ \prod_{n=1}^{\infty} \frac {(2n) \cdot (2n)}{(2n-1) \cdot (2n+1)} = \frac{\pi}{2} \]
루트를 씌우고 곱하는 개수가 무한대로 가지 않고 충분히 큰 상황을 가정하면
\[ \prod \frac {2n}{\sqrt{(2n-1) \cdot (2n+1)}} \approx \sqrt{\frac{\pi}{2}} \]
이때 첫 \( (2n-1)\)은 1이고, 마지막 \( (2n+1) \)은 따로 생각한다.
\[ \frac {\prod_{k=1}^{n} (2k)}{\sqrt{2n+1} \prod_{k=1}^{n} (2k-1)} \approx \sqrt{\frac{\pi}{2}} \]
\( \prod_{k=1}^{n} (2k) = 2^n n! \) 이고 \( \prod_{k=1}^{n} (2k-1) = \frac{(2n)!}{2^n n!} \) 이므로 \( n! \approx c \sqrt{n} \left(\frac{n}{e}\right)^n \) 를 대입하면,
\[ \frac{c}{2} = \sqrt{\frac{\pi}{2}} \]
즉,
\[c = \sqrt{2\pi} \]
따라서 증명이 완성되었다.
\[ n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n \]
ㅤ
ㅤ
처음 써본 수학 글이라 많이 불친절하고 더러울 것이다. 그래도 오버리프 문법 공부도 많이 하고 [더 메뉴] 논평 쓰다가 조금 미칠 뻔한 상태가 초심으로 약간 회복된 느낌이 든다.


Comments ()