Buffon's Needle Problem
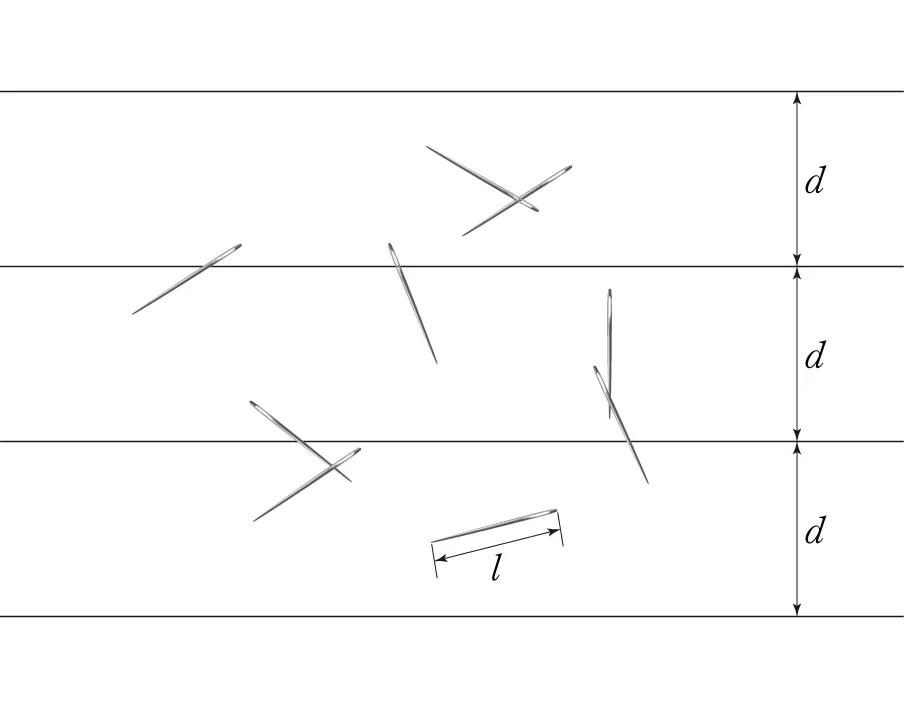
무한한 평면 위에 평행한 선들이 d의 간격을 두고 그어져 있다. 길이가 l인 바늘을 평면 위에 무작위로 떨어뜨린다. 바늘은 선에 걸칠 수도, 안 걸칠 수도 있다. 놀랍게도 이것으로 원주율 π를 계산할 수 있다.
원주율을 측정하는 방법은 정말 많다. 가장 전형적인 방법인 원의 둘레와 지름을 비교하는 방법과 원의 면적과 지름을 비교하는 방법 등이 있을 것이다. 이 중에는 원을 이용하지 않고 계산하는 방법도 있다. 원을 이용하지 않는 가장 대표적인 방법이 위에서 설명한 뷔퐁의 바늘(Buffon's Needle Problem)이다.
위에서 설명한 것과 같은 조건(단, \(d \ge l\))으로 바늘을 평면 위에 무작위로 떨어뜨렸을 때 바늘이 선에 걸칠 확률은 \(\frac{2l}{d\pi}\)이다. 왜일까?
증명
바늘을 무작위로 떨어뜨렸다. 그 바늘의 중심을 점 C라고 하자. 점C에서 가장 가까운 평행선과 더 가까운 쪽의 바늘의 끝을 A라고 하자. A에서 평행선과 평행한 직선 BC에 내린 수선의 발을 B라고 하자. C에서 가장 가까운 평행선에 내린 수선의 발을 H라고 하자. 바늘이 평행선과 이루는 각을 \(\theta\)(단, \(0 \le \theta \le \pi\))로 두자. 이해가 어려울 것 같아 그림을 첨부하였다.
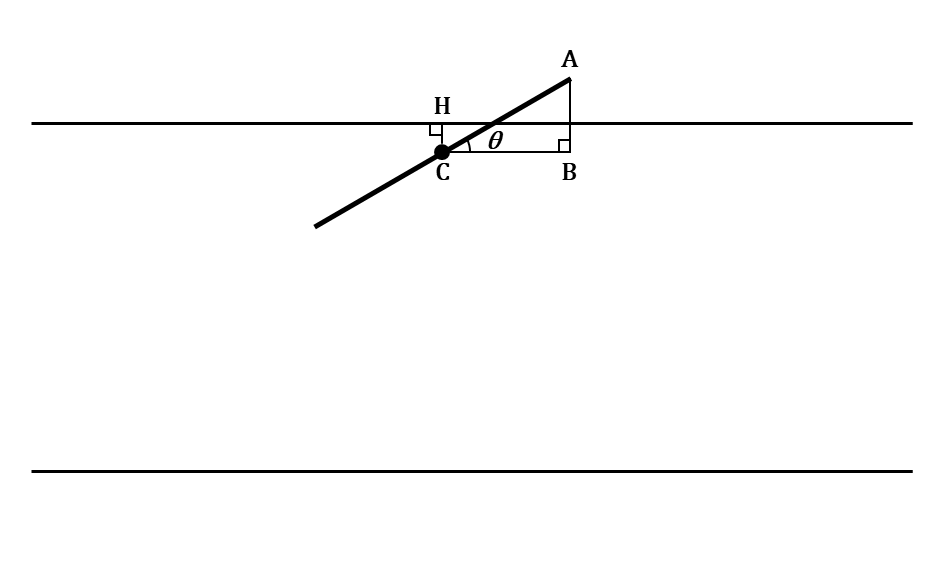
\(\overline{CH} \le d/2\)이고 바늘이 선에 걸칠 조건은 \(\overline{CH} \le \overline{AB}\)이다. 이때 \(\overline{AB} = \frac{l}{2}\sin \theta\)이기 때문에 결국 바늘이 선에 걸칠 조건은
\[\overline{CH} \le \frac{l}{2}\sin \theta\]
이제 x축이 \(\theta\)이고 y축이 \(\overline{CH}\)의 길이 \(x\)인 좌표평면 하나를 잡자. 전체 조건의 면 S와 바늘이 선에 걸칠 조건의 면 D는 다음과 같이 점들의 집합으로 나타낼 수 있다.
\[S = \left\{(\theta, x)\, \middle|\, 0 \le \theta \le \pi, 0 \le x \le \frac{d}{2}\right\}\]
\[D = \left\{(\theta, x)\, \middle|\, 0 \le \theta \le \pi, 0 \le x \le \frac{l}{2}\sin\theta\right\}\]
이제 바늘이 선에 걸칠 확률을 구하자. 확률은 \(S\)의 면적 \(S_S\)에 대한 \(D\)의 면적 \(S_D\)의 비로 표현될 수 있다. \(S\)는 직사각형이기에 \(S_S\)의 면적은 다음과 같이 구할 수 있다.
\[S_S = \pi \cdot \frac{d}{2}\]
\(D\)는 sin 함수와 \(\theta\)축으로 둘러싸여 있는 형태를 띠기에 정적분을 사용하여 면적을 구할 수 있다.
\[S_D = \int_0^\pi \frac{l}{2}\sin \theta \, d\theta = l\]
그러므로 바늘이 선에 걸칠 사건 A의 확률 P(A)는
\[P(A) = \frac{S_S}{S_D} = \frac{l}{\pi \cdot \frac{d}{2}} = \frac{2l}{d\pi}\]
실용적인가?
과거에는 원주율을 구할 때 자주 사용하던 방법이지만 훨씬 효과적이고 정확하게 원주율을 측정할 수 있는 현재 사용하기에는 다소 부적합하다. 그 이유는 너무 비효율적이기 때문이다. 이 방법으로 원주율을 측정하기 위해서는 바늘을 여러 번 떨어뜨리고 전체 횟수에 대한 선에 걸친 횟수의 비를 측정하며 점점 정확한 π에 수렴해야 하는데 이 수렴하는 속도가 대단히 느리다.
파이썬을 이용하여 시뮬레이션을 돌려보았다.
(떨어뜨린 횟수)번: (예상 원주율 값)
1번: 2.0
10번: 4.0
100번: 3.125
\(10^3\)번: 3.1397...
\(10^4\)번: 3.125
\(10^8\)번: 3.1420...
이렇게 무려 1억번의 시행을 했는데도 겨우 소수점 둘째자리까지 밖에 구하지 못했다. 당시에는 완벽한 원을 그리는 방법이 없었기에 이 방법이라도 사용한 것인데, 이제는 컴퓨터로 사실상 완벽한 원을 그릴 수 있는 상황에서는 다른 방법을 사용하는 것이 훨씬 효율적이다.
그래도 나름 원 사용 안하고 원주율을 측정할 수 있다는 점에 의의를 두자.





Comments ()