코시 응집 판정법
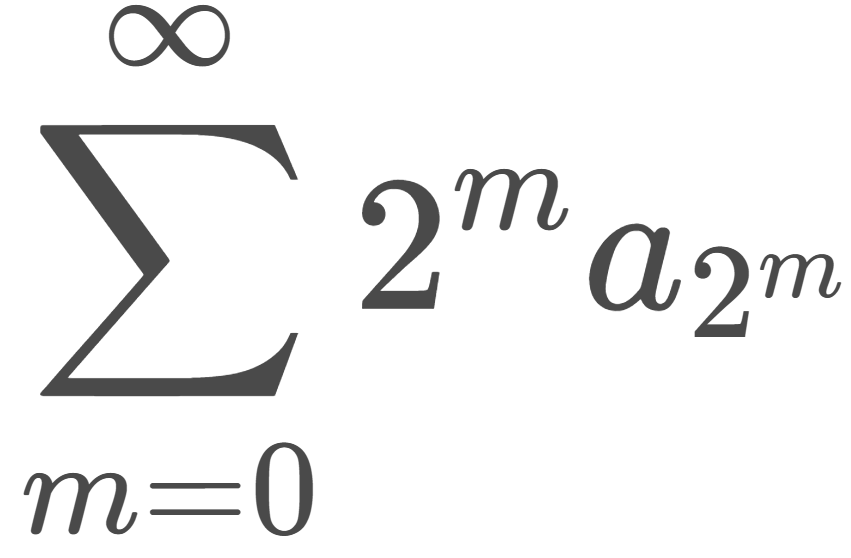
\( \{ a_n \}_{n=1}^{\infty}\,\,\, satisfy: \)
1. \( a_n \geq 0 \)
2. \( a_{n+1} \leq a_n \)
Than
\( \displaystyle \sum_{n=1}^{\infty} a_n \,\, \) converge \( \,\, \displaystyle \Leftrightarrow \sum_{m=0}^{\infty} 2^m a_{2^m} \,\, \) converge
ㅤ
ㅤ
증명
처음으로 \( \displaystyle \sum_{m=0}^{\infty} 2^m a_{2^m} \) 이 수렴한다는 조건 하에서 \( \displaystyle \sum_{n=1}^{\infty} a_n \) 의 수렴을 증명한다.
먼저 \( \displaystyle \sum_{n=1}^{\infty} a_n \) 의 수렴인 \( \displaystyle \lim_{N \to \infty} \sum_{n=1}^{N} a_n \) 과 \( \displaystyle \lim_{N \to \infty} \sum_{n=1}^{2^N} a_n \) 의 수렴은 동치이다.
\begin{equation*}
\begin{split}
\displaystyle \sum_{n=1}^{2^N} a_n &= a_1 + a_2 + a_3 + \cdots + a_{2^N} \\[2ex]
&= (a_1) +(a_2 + a_3) + (a_4 + a_5 + a_6 + a_7) + \cdots + ( a_{2^{N-1}} + \cdots + a_{2^{N}} ) \\[2ex]
& \leq (a_1) + (a_2 + a_2) + (a_4 + a_4 + a_4 + a_4) + \cdots + ( a_{2^{N-1}} + a_{2^{N-1}} + \cdots + a_{2^{N-1}}) \\[2ex]
&= \sum_{m=0}^{N-1} 2^m a_{2^m} \\[2ex]
\end{split}
\end{equation*}
이 경우에는 \( \displaystyle \sum_{m=0}^{\infty} 2^m a_{2^m} \) 이 수렴하므로 \( \displaystyle \sum_{m=0}^{N-1} 2^m a_{2^m} \) 가 모든 \( N \) 에 대하여 유계이다. 그렇다면 위 부등식은 가장 아래 항이 유계일 때 \( \displaystyle \sum_{n=1}^{2^N} a_n \) 가 유계임을 담고있다.
따라서 \( \displaystyle \sum_{n=1}^{2^N} a_n \) 는 모든 항이 양수인 급수이면서, 즉 단조 증가하는 수열이면서 유계, 즉 상한을 가지므로 단조수렴 정리에 의해 \( \displaystyle \sum_{n=1}^{\infty} a_n \) 은 수렴한다.
ㅤ
그 다음에는 \( \displaystyle \sum_{n=1}^{\infty} a_n \) 의 수렴이 \( \displaystyle \sum_{m=0}^{\infty} 2^m a_{2^m} \) 의 수렴으로 이어지는가를 보인다. 그렇다면 양방향 화살표가 보여지며 본 정리의 완전한 증명이 된다.
\begin{equation*}
\begin{split}
\sum_{m=0}^{N} 2^m a_{2^m} &= a_1 + 2 a_2 + 4 a_4 + \cdots + 2^N a_{2^N} \\[2ex]
&= (a_1) + (a_2 + a_2) + (a_4 + a_4 +a_4 +a_4) + \cdots + (a_{2^N} + a_{2^N} \cdots + a_{2^N} ) \\[2ex]
& \leq (a_1) + (a_1 + a_2) + (a_2 + a_3 +a_3 +a_4) + (a_4 + a_5 + a_5 +\cdots +a_7+a_8) \\[2ex] & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \cdots + (a_{2^{N-1}} + a_{2^{N-1} +1} + a_{2^{N-1} +1} + a_{2^{N-1} +2} + a_{2^{N-1} +2} \cdots + a_{2^N} ) \\[1.5ex]
&= 2 (a_1 + a_2 + \cdots + a_{2^{N}-1} + a_{2^N} ) - a_{2^N} \\[2ex]
& \leq 2 \sum_{n=1}^{2^N} a_n
\end{split}
\end{equation*}
이때 \( \displaystyle \sum_{n=1}^{\infty} a_n \) 가 수렴한다는 것은 \( \displaystyle \sum_{n=1}^{2^N} a_n \) 가 유계임을 의미하고 즉 이는 \( \displaystyle \sum_{m=0}^{N} 2^m a_{2^m} \) 의 유계성을 부여한다. 따라서 이 경우에도 단조수렴정리에 의해 \( \displaystyle \sum_{m=0}^{\infty} 2^m a_{2^m} \) 는 수렴한다.
ㅤ
이것으로 단조 감소 양급수, \( \displaystyle \sum_{n=1}^{\infty} a_n \) 의 수렴과 \( \displaystyle \sum_{m=0}^{\infty} 2^m a_{2^m} \) 의 수렴은 동치임을 보였다.
ㅤ
ㅤ
응용
코시의 응집 판정법은 급수에서 극히 일부의 항만을 가지고 수렴성을 판단할 수 있는 판정법이다. 다르게 말하면 특정 조건을 만족하는 항들에 대해서 급수의 합을 알 때 그 특수한 조건이 원하는만큼 타이트해도 판정 조건을 만족할 수 있다고 할 수 있다.
ㅤ
먼저 적분 판정법을 사용하지 않고 급수의 \( p- \)테스트를 증명할 수 있다. \( p- \)테스트란,
1. \( \,\,\, p \in \mathbb{R} \)
\( \displaystyle \sum_{n=1}^{\infty} \frac{1}{n^p}\,\, \) converge \( \,\,\, \Leftrightarrow \,\,\, p>1 \)
실수 \( p \) 에 대하여 급수 \( \displaystyle \sum_{n=1}^{\infty} \frac{1}{n^p} \)의 수렴 조건은 \( \displaystyle \sum_{n=0}^{\infty} 2^n \frac{1}{(2^n)^p} \) 의 수렴과 동치이다.
\[ \sum_{n=0}^{\infty} 2^n \frac{1}{(2^n)^p} = \sum_{n=0}^{\infty} \left( \frac{1}{2^{p-1}} \right)^n \]
이므로 해당 등비급수의 수렴 조건인 \( \displaystyle \left| \frac{1}{2^{p-1}} \right| < 1 \) 즉, \( p>1\) 이 구하려는 \( p \) 급수, \( \displaystyle \sum_{n=1}^{\infty} \frac{1}{n^p} \) 의 수렴 조건이 된다.
ㅤ
이를 그대로 확장하면 급수
\[ \sum_{n=2}^{\infty} \frac{1}{ n^{p} \ln n } \]
의 수렴 조건도 구할 수 있다.
먼저 이 급수의 수렴성은
\[ \sum_{n=1}^{\infty} 2^{n} \frac{1}{ (2^{n})^{p} \ln (2^{n} ) } = \frac{1}{ \ln 2 } \sum_{n=1}^{\infty} \left( \frac{1}{ 2^{p-1} } \right)^{n} \frac{1}{n} \]
의 수렴 조건과 같다. 이 때 \( \displaystyle \left| \frac{1}{2^{p-1}} \right| > 1 \) 라면 급수의 일반항이 발산하고 \( \displaystyle \left| \frac{1}{2^{p-1}} \right| = 1 \) 이라면 \( \displaystyle \sum_{n=1}^{\infty} \frac{1}{n} \) 은 \( p- \)테스트에 의해 발산한다.
따라서 해당 급수는 \( p > 1 \) 가 수렴의 필요충분조건이다.
ㅤ
또
\[ \sum_{n>e} \frac{1}{n^p ( \ln n ) ( \ln \ln n ) } \]
의 수렴이 있다. 먼저 수렴 발산에 초기값과 상수 곱은 중요하지 않으므로
\[ \sum_{n>2} 2^n \frac{1}{2^{np} n \ln n } = \sum_{n>2} \frac{1}{n \ln n } \left( \frac{1}{ 2^{p-1} } \right)^n \]
으로 쓸 수 있고 이는 등비 수열 항에서 공비가 \( 1\)보다 크면 발산, \( 1 \)이면 \( \displaystyle \sum_{n=2}^{\infty} \frac{1}{n^{p} \ln n } \) 가 되어 앞선 증명에 의해 발산한다.
결국 위 급수의 수렴 조건 또한 \( p > 1 \) 이 된다.
ㅤ
이 논리를 반복하면 결국 \( \ln \) 을 \( k \) 번 합성한 함수까지의 급수
\[ \sum_{n>e^{e^{e^{\cdots^e}}}} \frac{1}{n^p ( \ln n )( \ln \ln n )( \ln \ln \ln n ) \cdots ( \ln \ln \cdots \ln n ) } \]
의 수렴 조건은 \( p > 1 \) 임을 밝힐 수 있다.




Comments ()