제타함수의 해석적 연속

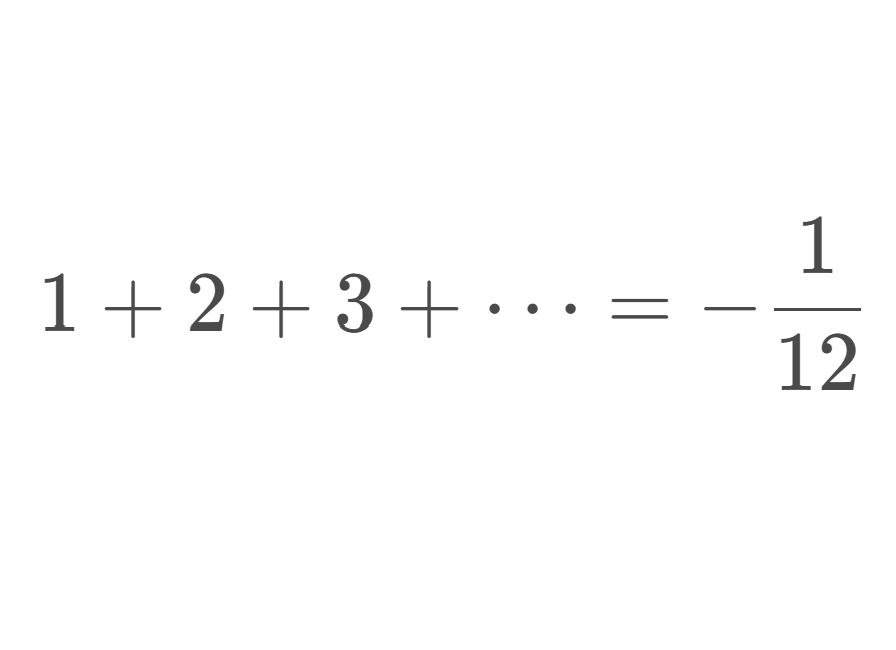
인터넷 등지 수학 관련 자료에서 이 수식을 한 번쯤은 본 적이 있을 것이다.

\[1+2+3+ \cdots = - \frac{1}{12}\]

이러한 수식은 발산하는게 당연한 급수의 값을 합리적으로 정할 수 있다는 사실을 통해 수학의 자유로움을 단적으로 보여준다. 구체적인 수학적 배경은 완전히 다르지만 발산하는 그란디의 급수의 값을 정할 수 있는 체사로합의 방법과 비슷한 인상을 띈다. (Kim Kyudong의 글 참고)

\[1-1+1-1+1- \cdots = \frac{1}{2} \]

다시 본론으로 돌아오자면 가장 위에 있는 급수의 값은 주로 라마누잔 합의 방법으로 구한다 소개된다. 그러나 해당 글에서는 다음과 같이 정의되는 리만 제타함수를 활용하여 값을 부여하는 방법을 소개한다.

\[ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} \,\,\,\,\,\,\,\,\,\,\, (\operatorname{Re} (z) > 1) \]

보이는 듯이 리만 제타함수의 정의역은 실수부가 1보다 큰 복소수로 제한된다. 그러니

\[ 1+2+3+ \cdots = \sum_{n=1}^{\infty} n = \zeta(-1) \]

은 말이 되지 않는 수식이다. 따라서 우리가 가지고 있는 제타함수의 식을 그대로 활용할 수 없다. 그러니 해석적 연속이라는 기법을 사용하여 해당 급수의 값을 정의하는 방법 중 하나를 얻는다.

먼저 복소평면 위 한 점에서의 해석함수란, 그 점을 중심으로 한 원판(\( B = \{ z : |z-z_0| < r \} \))에서 유효한 테일러 급수를 가진다는 것으로 정의한다. 그리고 한 영역에서 해석적인 함수는 그 영역 위의 모든 점에서 해석적인 함수를 의미한다.

해당 개념을 더 잘 이해하기 위해 잠시 실수로 옮겨 본다.

\[ f_1(x) = \sum_{n=0}^{\infty} x^n \]

는 \( D_1 = (-1,\,1) \) 에서 유효한 함수이다. 이때 \( D_2 = \mathbb{R} - \{1\} \) 에서 정의된 함수 \(f_2 = \dfrac{1}{1-x} \) 를 잡는다. \( f_1 \) 과 \( f_2\)는 \( D_1 \cap D_2 = (-1, \, 1) \) 에서 같은 값을 가진다. 따라서 \( f_2\)는 \(f_1\)의 해석적 연속이라 할 수 있다. 그리고 이를 이용해 다음 급수의 값을 정의할 수 있다.

\[ 1+2+4+8+16+ \cdots = \frac{1}{1-2} = -1 \]

그러니 우리는 리만 제타함수의 -1을 포함한 영역으로의 해석적 연속을 구해야 한다. 일단 리만 제타함수가 실수부가 1보다 큰 반평면에서 해석적이라는 사실은 자명하므로 받아들인다.

먼저 다음 정리를 살펴보자.

Theorem는 자연스럽게 해석적 연속의 유일성을 부여한다.

우리가 바라는 리만 제타함수의 해석적 연속은 기존의 것의 정의역 전체인 반평면(\(\operatorname{Re}(z)>1\))에서 급수식과 값이 같아야 한다. 그러니 두 해석적 연속이 존재한다 하면 해당 반평면을 두 함수값이 항상 같은 영역 영역으로 가지게 된다. 한편 두 해석함수의 정의역은 모두 \( \mathbb{C} -\{1\} \) 이므로 위의 \(D\)를 \( \mathbb{C} -\{1\} \) 으로 둔다. 반평면 (\(\operatorname{Re}(z)>1\))에서 함수값들이 완전히 같으므로 위 조건을 만족하는 수열이 존재한다. 그렇다면 Theorem에 의해 이 둘은 \(D\)에서, 즉 정의역 전체에서 같은 함수여야 한다.

아래는 증명의 간단한 스케치를 담았다.

Prove of Theorem

먼저 \( g(z) = f_2(z)-f_1(z) \) 로 놓으면 \( g\)는 해석적이면서 \( z_0 \) 로 수렴하는 수열이 다음을 만족한다.

\[ \forall n \in \mathbb{N} \,\,:\,\, g(z_n) = 0 \]

먼저 한 작은 원판 \( B = \{ z : |z-z_0| < r \} \)에서 정리를 증명해보자.

를 만족한다. 해석함수이므로 \( z_0\)를 중심으로 한 원판에서 테일러 전개할 수 있다.

\[ g(z) = a_0 + a_1(z-z_0) +a_2 (z-z_0)^2 + a_3(z-z_0)^3 + \cdots \]

해석함수는 연속함수이므로

\[ a_0 = g(z_0) = g \left( \lim_{n \to \infty} z_n \right) = \lim_{n \to \infty} g(z_n) = \lim_{n \to \infty} 0 = 0 \]

이다.

\[ g(z) = a_1(z-z_0) +a_2 (z-z_0)^2 + a_3(z-z_0)^3 + \cdots \]

이때 다른 해석함수를 둔다. 테일러 급수가 존재하므로 해석함수다.

\[ g_1(z)= \frac{g(z)}{z-z_0} = a_1 + a_2(z-z_0) + a_3 (z-z_0)^2 + \cdots \]

(정확히는 위 가운데 정의에서 \( g_1(z_0) = a_1 \) 를 이용해 구멍을 채우면 된다. )

임의의 자연수 \( n\)에 대하여 \( g_1(z_n) = \dfrac{g(z_n)}{z_n-z_0} = 0 \) 이다.

따라서 위와 같은 논리로

\[ a_1 = g_1(z_0) = g_1 \left( \lim_{n \to \infty} z_n \right) = \lim_{n \to \infty} g_1(z_n) = \lim_{n \to \infty} 0 = 0 \]

이를 반복하여 귀납법을 사용하면 모든 테일러 계수가 0임을 확인할 수 있다. 따라서 \( g\)는 원판 \( B_1\)에서 항등적으로 0이다.

그리고 임의의 연결된 영역 \( D\)에서 정리를 증명해보자. \( D\)는 영역이므로 정의에 의해 연결된 열린집합이다. 열린집합이므로 모든 점이 inner point( 그 점을 중심으로 한 원판이 존재하여 그 원판이 \( D\) 에 포함되도록 반지름을 설정할 수 있는 점) 이다.

연결되어 있으므로 \( z_0\)와 \( D\)위의 임의의 점 \( z_f\)를 잇는 곡선 \( \gamma\)가 존재한다. 이 \( \gamma\)를 기준으로 원판들을 이어붙여 \(z_f\)까지 도달하는 것을 생각한다.

먼저 \( z_0 \)를 중심으로 하고 \( D\)에 포함되는 가장 큰 원판을 잡는다. 그리고 원판 \( B_0\)와 \( \gamma\)의 교집합에서 \( z_f\)쪽으로 적당히 많이 다가간 점 \( w_0\)를 잡는다. 그리고 \( w_0\)를 둘러싼 적당히 작은 원판을 포함하고 \( \gamma\)위에 중심이 있으면서 \( D\)에 포함되는 가장 큰 원판을 잡는다. 새로 잡은 원판\( B_1\)의 중심을 \( z_1 \)이라 하자. 이 경우 \( g(z)\)는 \( B_0\)에서 항등적으로 0이므로 \( B_0\)에 포함되어 \( w_0\)로 수렴하는 수열은 항상 \( g(w_n)\)을 모두 0으로 만든다. 그 수열 중 \( B_0 \cap B_1\)에 포함되는 수열을 잡는다면 앞선 결과로 인해 \( g\)의 값은 \( B_1\)에서 항등적으로 0임을 증명할 수 있다.

이 과정을 \( z_1 \)에 대해 \( \gamma\)위에 있는 \( z_2 \)를 잡아 이를 중심으로 하는 원판 \( B_2\)에서 \( g\)의 값을 항등적으로 0이 되도록 반복 할 수 있다.

이를 반복하면 \( z_f\)를 포함하는 원판, \( B_f\)를 통해 \( g(z_f)\)가 0임을 보일 수 있다. \( z_f\)는 \( D\)위의 임의의 점이므로 결국 \( D\)에서 함수 \( g\)가 항등적으로0임을 보였다.

해석적 연속의 유일성이 보장되었으니 이를 실제로 구하는 과정을 살펴보자.

앞서 푸리에 해석과 연관이 깊은 함수인 세타함수를 살펴보자.

\[ \theta (t) = \sum_{n \in \mathbb{Z}} e^{-\pi n^2 t} \]

으로 정의되는 함수이다. 이때 푸아송 합공식을 적용하면 다음을 얻을 수 있다.

이는 추후 대칭적인 제타함수의 성질을 수식으로 보이는 데 관여한다. 그리고 당장은 세타함수의 증감 정도를 파악하는데 도움을 준다.

푸아송 합 공식은 당장에 증명하기는 어려우니 직관적이지는 않더라도 받아드리고 넘어간다. (도와줘요 Kim Kyudong)

Prove of Lemma1

이때는 좌변이 \( \theta (x) \) 가 되도록 \( f(t) = e^{- \pi t^2 x} \)로 잡는다. 그리고 이 함수의 푸리에 변환을 계산한다.

\begin{equation*}
\begin{split}
\hat{f} (k) &= \int_{-\infty}^{+\infty} f(t) e^{-2\pi i k t} dt \\[2ex]
&= \int_{-\infty}^{+\infty} e^{-\pi (xt^2 + 2 i k t)} dt \\[2ex]
&= \int_{-\infty}^{+\infty} e^{-\pi x \left( t + \frac{ik}{x} \right)^2 - \frac{\pi k^2}{x}} dt \\[2ex]
&= e^{ - \frac{\pi k^2}{x}} \int_{-\infty}^{+\infty} e^{-\pi x \left( t + \frac{ik}{x} \right)^2} dt \\[2ex]
\end{split}
\end{equation*}

이때는 변수가 허수부분으로 평행이동 되어 있기 때문에 단순한 치환으로 답을 구하는 것은 옳지 않다. 따라서 이때는 경로 적분에 대한 코시 구르사 정리를 사용한다.

\( f(z) = e^{-\pi x z ^2} \) 는 자명하게 해석적이고 이를 이용해 큰 양수 \( R_1, \, R_2 \) 다음과 같은 폐곡선을 고안한다.

위 그림은 \( \frac{ik}{x} = 2i \, , \,\, R_1 = 5 \, , \,\, R_2 = 6 \) 에 대하여

\begin{equation*}
\begin{split}
\gamma &= \Gamma_1+\Gamma_2+\Gamma_3+\Gamma_4 \\[2ex]
&= [-R_2, \, R_1] + \left\{ \operatorname{Re}(z) = R_1 \, , \,\, 0 \leq \operatorname{Im}(z) \leq \frac{k}{x} \right\} \\[2ex]
& \,\,\,\, - \left\{ \operatorname{Im}(z) = \frac{k}{x} \, , \,\, R_1 \leq \operatorname{Im}(z) \leq R_2 \right\} - \left\{ \operatorname{Re}(z) = -R_2 \, , \,\, 0 \leq \operatorname{Im}(z) \leq \frac{k}{x} \right\} \\[2ex]
\end{split}
\end{equation*}

을 표현한 것이다.

이때 마이너스는 폐곡선의 방향이 반대임을 의미하고 쓴 것이다.

\[ \oint_{\gamma} f(z) dz = \int_{\Gamma_1} f(z) dz +\int_{\Gamma_2} f(z) dz + \int_{\Gamma_3} f(z) dz + \int_{\Gamma_4} f(z) dz = 0 \]

에서 두번째와 네번째의 적분은 \( R_1\) 과 \(R_2\)가 무한대로 가는 극한에서 0으로 가고

\[ \lim_{R_1 , R_2 \to \infty} \int_{\Gamma_1} f(z) dz = \int_{-\infty}^{+\infty} e^{-\pi x t^2} dt \]

\[ \lim_{R_1 , R_2 \to \infty} \int_{\Gamma_4} f(z) dz = \int_{+\infty}^{-\infty} e^{-\pi x \left( t + \frac{ik}{x} \right)^2} dt \]

이므로 우리가 구하려는 적분은 실수로 평행이동한 일반적인 가우스 적분의 꼴과 그 값이 같다.

이때 알아두어야 할 것이 \( R_1\) 과 \(R_2\)가 서로 독립적으로 무한대로 가는 극한을 적용한다. 이상적분의 정의인

\[ \int_{-\infty}^{+\infty}f(t) dt = \int_{-\infty}^{a}f(t) dt+\int_{a}^{+\infty}f(t) dt \]

를 참고하기 바란다.

\[ \hat{f} (k) = e^{ - \frac{\pi k^2}{x}} \int_{-\infty}^{+\infty} e^{-\pi x \left( t + \frac{ik}{x} \right)^2} dt = e^{ - \frac{\pi k^2}{x}} \int_{-\infty}^{+\infty} e^{-\pi x t^2} dt = e^{ - \frac{\pi k^2}{x}} \sqrt{\frac{\pi}{\pi x}} \]

따라서 이 결과를 푸아송 합 공식에 대입하기만 하면 증명이 완료된다.

\[ \sum_{n \in \mathbb{Z}} f(n) = \sum_{k \in \mathbb{Z}} \hat{f}(k) \]

\[ \theta (x) = \sum_{k \in \mathbb{Z}} \left( e^{ - \frac{\pi k^2}{x}} \frac{1}{\sqrt{x}} \right) = \frac{1}{\sqrt{x}} \theta \left( \frac{1}{x} \right) \]

먼저 세타함수의 급수의 각 항은 \( n\)에 대한 우함수이므로

\[ \frac{\theta(x) - 1}{2} = \sum_{n=1}^{\infty} e^{-\pi n^2 x} =\psi(x)\]

라 정의하자.

그리고 다음과 같은 적분을 생각해보자.

\[ I= \int_{0}^{\infty} x^{\frac{s}{2} -1} \psi(x) dx \]

먼저 이 적분은 수렴한다.

아래 부등식

\[ \psi(x) = \sum_{n=1}^{\infty} e^{-\pi n^2 x} \leq \sum_{n=1}^{\infty} e^{-\pi n x} = \frac{e^{-\pi x}}{1-e^{-\pi x}} \]

에서 \( x \)가 충분히 크다면

\[ \psi(x) \leq C e^{-\pi x} \]

이기 때문이다.

\[ I = \int_{0}^{\infty} x^{\frac{s}{2} -1} \sum_{n=1}^{\infty} e^{-\pi n^2 x} dx \]

에서 앞선 논리로 급수와 적분의 순서를 바꿀 수 있다.

\[ I = \sum_{n=1}^{\infty} \int_{0}^{\infty} x^{\frac{s}{2} -1} e^{-\pi n^2 x} dx \]

이는 간단한 치환적분을 사용하여 감마함수를 통해 나타낼 수 있다.

\begin{equation*}
\begin{split}
I &= \sum_{n=1}^{\infty} \pi ^{-s/2} \Gamma \left( \frac{s}{2} \right) n^{-s} \\[2ex]
&= \pi ^{-s/2} \Gamma \left( \frac{s}{2} \right) \sum_{n=1}^{\infty} n^{-s} \\[2ex]
&= \pi ^{-s/2} \Gamma \left( \frac{s}{2} \right) \zeta(s) \\
\end{split}
\end{equation*}

이제는 식 구하기의 마지막 단계로 계산한 적분이 \(s = \dfrac{1}{2}\)에 대한 점대칭 함수임을 보이면 된다. 아래의 대칭식이 제타함수의 해석적 연속을 위한 함수 방정식이 된다.

Prove of Lemma2

Lemma1이 보이는 항등식에 의해 얻은

\[\psi(x) = \frac{\theta(x) - 1}{2} = \frac{\frac{1}{\sqrt{x}} \theta \left( \frac{1}{x} \right) - 1}{2} = \frac{1}{2} x^{-1/2} \theta \left( \frac{1}{x} \right) - \frac{1}{2} = x^{-1/2} \psi \left( \frac{1}{x} \right) + \frac{1}{2}x^{-1/2} - \frac{1}{2}\]

를 대입하고 조금 조작한다.

\begin{equation*}
\begin{split}
\xi(s) &= \int_{0}^{1} x^{\frac{s}{2} -1} \psi(x) dx + \int_{1}^{\infty} x^{\frac{s}{2} -1} \psi(x) dx \\[2ex]
&= \int_{0}^{1} x^{\frac{s}{2} -1} \left( x^{-1/2} \psi \left( \frac{1}{x} \right) + \frac{1}{2}x^{-1/2} - \frac{1}{2} \right) dx + \int_{1}^{\infty} x^{\frac{s}{2} -1} \psi(x) dx \\[2ex]
\end{split}
\end{equation*}

일단 앞의 항의 뒤쪽 두 적분인

\begin{equation*}
\begin{split}
\frac{1}{2} \int_{0}^{1} x^{\frac{s-1}{2} -1} dx &= \frac{1}{s-1} \\[3ex]
- \frac{1}{2} \int_{0}^{1} x^{\frac{s}{2} -1} dx &= -\frac{1}{s} \\
\end{split}
\end{equation*}

는 따로 구해 빼놓고

\[ \int_{0}^{1} x^{\frac{s-1}{2} -1} \psi \left( \frac{1}{x} \right) dx \]

에는 \( x \to \dfrac{1}{x} \) 의 치환을 적용해

\[ \int_{1}^{\infty} x^{-\frac{s-1}{2} -1} \psi \left( x \right) dx \]

로 구한다. 결국

\begin{equation*}
\begin{split}
\xi(s) &= \frac{1}{s-1} -\frac{1}{s} + \int_{1}^{\infty} \left( x^{\frac{s}{2} -1} + x^{-\frac{s-1}{2} -1} \right) \psi(x) dx \\[2ex]
&= - \left( \frac{1}{s} + \frac{1}{1-s} \right) + \int_{1}^{\infty} \left( x^{\frac{s}{2} -1} + x^{\frac{1-s}{2} -1} \right) \psi(x) dx \\
\end{split}
\end{equation*}

이므로 Lemma2가 성립한다.

\( \xi(s) = \xi(1-s) \) 에서 다음을 얻는다.

\[ \pi ^{-s/2} \Gamma \left( \frac{s}{2} \right) \zeta(s) = \pi ^{-(1-s)/2} \Gamma \left( \frac{1-s}{2} \right) \zeta(1-s) \]

이 식에서 특정 점의 제타함수값을 간편하게 얻기 위해서 다음 두 식을 이용해 \( \zeta(s) \)에 대해 정리된 식을 얻는다.

이 둘을 대입하고 정리하면 다음을 얻을 수 있다. Theorem에 의해 아래의 함수가 제타함수의 유일한 해석적 연속임을 보장받는다.

\[ \zeta(s) = 2^s \pi^{s-1} \sin(\frac{\pi s}{2}) \Gamma(1-s) \zeta(1-s) \]

\( s = -1\) 를 대입하면 우리가 원하는 값을 구할 수 있다.

\begin{equation*}
\begin{split}
\zeta(-1) &= \frac{1}{2} \pi^{-2} \sin(\frac{-\pi}{2}) \Gamma(2) \zeta(2)\\[1.5ex]
&= \frac{1}{2} \pi^{-2} \sin(\frac{-\pi}{2}) \frac{\pi^2}{6} \\[1.5ex]
&= -\frac{1}{12} \\
\end{split}
\end{equation*}

따라서 해석적 연속의 관점에서

\[1+2+3+ \cdots \neq \zeta(-1) = - \frac{1}{12}\]

이라 쓸 수 있다.