Introduction

오늘은 오일러 공식을 이끌어내는 5가지 방법을 알아보도록 하자.

제목이 <오일러 공식을 증명하는 5가지 방법>이 아니라 <오일러 공식을 이끌어내는 5가지 방법>인 이유는 엄밀한 증명을 위해서는 고급 수학을 다뤄야 하기 때문이다. 그래서 수학적 엄밀함 보다는 아이디어에 초점을 맞추고 글을 읽도록 하자.

I. 테일러 급수

각 함수를 테일러 급수로 나타내면
\[
e^x = \sum^{\infty}_{n=0}\frac{x^n }{n!}
\]\[
\sin {x} = \sum^{\infty}_{n=0}\frac{(-1)^{n}x^{2n+1} }{(2n+1)!}
\]\[
\cos {x} = \sum^{\infty}_{n=0}\frac{(-1)^{n}x^{2n}}{(2n)!}
\]
이때 \(\displaystyle\cos{x}+i\sin{x} = \sum^{\infty}_{n=0}\frac{(ix)^n }{n!} = e^{ix}\)이다.

\[\therefore e^{ix}=\cos{x}+i\sin{x}\]

하지만, 이것이 완전한 증명이 되기 위해서는 두 무한급수의 더하는 순서를 바꿔도 바뀐 무한급수가 같은 값으로 수렴함을 보여야 한다. 사실 그럴 수도 있고 아닐 수도 있다. 이게 필자가 말한 수학적 엄밀함이다.

II. 1계 미분방정식

\(f(x) = \cos{x} + i\sin{x}\)라고 하자. \(f'(x) = -\sin{x} + i\cos{x}\)이다. 우리는
\(\frac{f'(x)}{f(x)} = i\) 임을 알 수 있다. 양변을 적분하면 \(\ln(f(x)) = ix + C\)이다. \(f(x)=e^{ix+C}\)인데, \(f(0) = 1\)이므로 \(C = 0\)이다.

\[\therefore e^{ix}=\cos{x}+i\sin{x}\]

III. 2계 미분방정식

II에서 $f(x)$를 두 번 미분하자. $f''(x) = -\cos{x}-i\sin{x}$이다. 우리는 $f''(x)+f(x)=0$이라는 미분방정식을 얻는다. 이것의 특성다항식은 $x^{2}+1$이므로 미분방정식의 해는 $Ae^{ix}+Be^{-ix}$이다. $f(0)=1, f'(0)=i$를 이용해 $A, B$를 구하면 $A=1, B=0$이다.

\[\therefore e^{ix}=\cos{x}+i\sin{x}\]

IV. 등속원운동

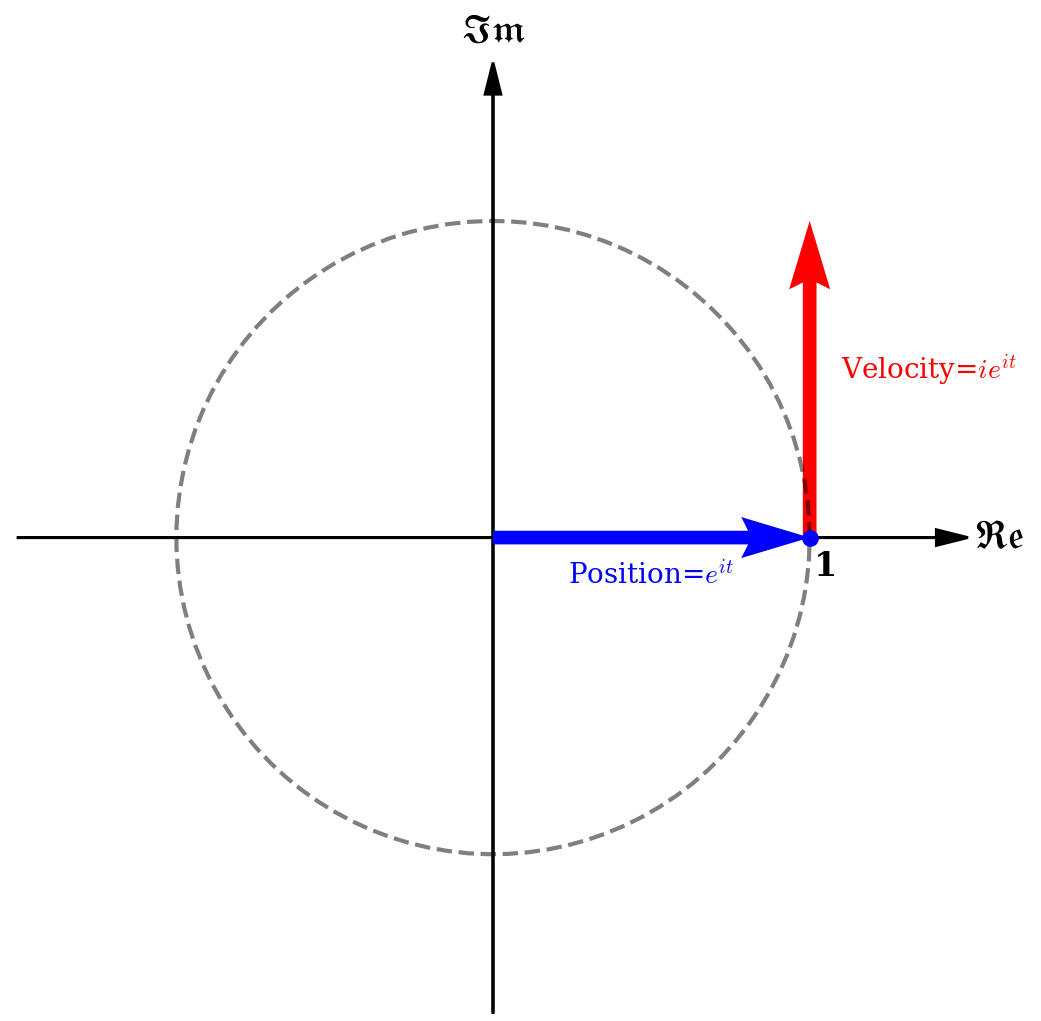
복소평면에서 한 입자의 위치를 $e^{it}$로 두자. 속도는 $ie^{it}$이다. 즉, 속도=$i\times$위치이다. 이로부터 속도가 위치에 직교하며, 크기가 항상 1임을 알 수 있다. 즉, 입자는 등속원운동을 한다. 등속원운동의 반지름을 구해보자. $t=0$일 때 위치는 1이다. 결국 등속원운동의 반지름은 1이다. 그런데 이 운동을 복소평면 상의 좌표성분으로 분해하면 시간에 따른 입자의 위치는 $\cos{t}+i\sin{t}$이다.

\[\therefore e^{ix}=\cos{x}+i\sin{x}\]

V. 드 무아브르 정리

$\displaystyle e^{ix}=\lim_{n\rightarrow\infty}{(1+\frac{ix}{n})^n}$이므로 충분히 큰 N에 대해 $ e^{ix}\approx{(1+\frac{ix}{N})^N}$로 둘 수 있다.

그런데 충분히 큰 N에 대해 $\sin{\frac{x}{N}}\approx\frac{x}{N}, \cos{\frac{x}{N}}\approx1$이다.

이것을 대입하면 $e^{ix}=(\cos{\frac{x}{N}}+i\sin{\frac{x}{N}})^N$이다.

드 무아브르 정리에 의해 $(\cos{\frac{x}{N}}+i\sin{\frac{x}{N}})^N=\cos{x}+i\sin{x}$이다.

\[\therefore e^{ix}=\cos{x}+i\sin{x}\]

결론

오늘 우리는 오일러 공식을 이끌어내는 5가지 방법을 알아보았다. 한 공식을 유도하는 방법이 이렇게나 다양하다는 사실이 놀랍지 않은가? 다음에 나올 피타고라스 정리를 증명하는 $n$가지 방법도 많은 관심 부탁한다.