Stirling's Approximation

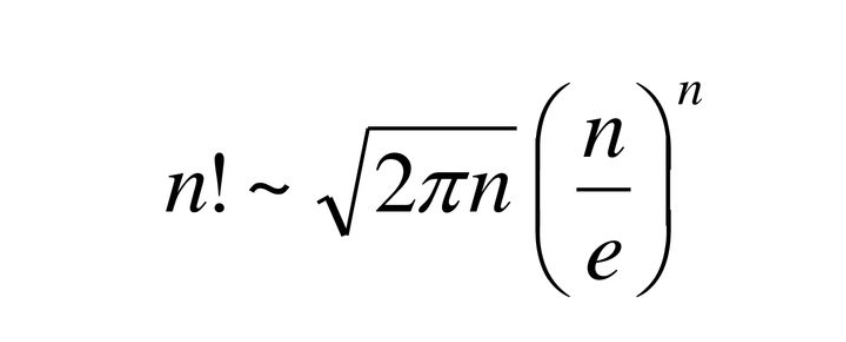
Introduction

위에서 언급된 두 글에서는 각각 다른 방법으로 스털링 근사를 유도했다. 하나의 글에서는 팩토리얼을 감마 함수로 표현하고 감마 분포의 성질을 이용하여 스털링 근사를 유도하였고, 다른 글에서는 팩토리얼에 자연로그를 취한 후 리만합을 이용하여 스털링 근사를 유도해내었다. 다음은 각각의 방법에 대한 상세 설명이다.

Proof 1 (감마 함수 이용)

먼저, 증명을 위해서 \(n!\) 을 감마 함수 표현으로 고치도록 하자.

\[n! = \Gamma(n+1) = \int\nolimits_{0}^{\infty}x^n e^{-x}\mathrm{d}x\]

이때, 피적분 함수가 감마 분포를 따른다는 것을 알 수 있다.

감마 분포는 \(n\) 이 매우 클 경우 중심 극한 정리에 의해 정규 분포로 근사될 수 있다. 그렇다면 근사를 위해서 우리가 더 다루기 쉬운 꼴인 정규 분포의 형태로 식을 바꿔 보자.

피적분 함수의 꼴을 바꿔보면,

\[x^n e^{-x} = e^{n\ln x -x}\]

이제 \(y = x-n\)으로 치환하고 식을 전개하면,

\[n\ln x -x = n\ln(n+y)-n-y\\ \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space=n\ln\left[n\left(1+\frac{y}{n}\right)\right]-n-y\\ \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space=n\ln n -n + n\ln\left(1+\frac{y}{n}\right)-y\]

이제, 여기서 정규 분포의 형태를 얻기 위해서 \(\ln\left(1+\frac{y}{n}\right)\) 를 테일러 전개하여 2 차 항까지 나타내면,

\[\ln\left(1 + \frac{y}{n}\right) \approx \frac{y}{n} - \frac{1}{2} \left(\frac{y}{n}\right)^2\]

위의 식을 대입하여 최종적인 피적분 함수의 근사식을 구하면,

\[x^n e^{-x} \approx n^n e^{-n} e^{-\frac{y^2}{2n}}\]

이때 감마 분포를 정규분포에 근사하였기 때문에, \(y<0\)인 영역은 0에 가깝다. 따라서 모든 \(y\)에 대하여 적분하면,

\[n! = \int_0^\infty x^n e^{-x} \,\mathrm{d}x \approx n^n e^{-n} \int_{-\infty}^\infty e^{-\frac{y^2}{2n}} \, \mathrm{d}y = n^n e^{-n} \sqrt{2\pi n}\]

Proof 2 (리만합 이용)

팩토리얼은 다음과 같이 비율적으로 근사된다.

\[ n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n \]

곧,

\[ \lim_{n \to \infty} \, \frac{n!}{\sqrt{2\pi n} \left(\frac{n}{e}\right)^n} = 1\]

증명의 시작은 곱을 합으로 바꾸는 것이다. 즉 \( \ln \)을 사용한다.

\[ \ln(n!) = \sum_{k=1}^{n} \ln(k) \]

이때 우변을 보면 리만 적분의 근사식처럼 보인다.

\[ \int_{a}^{b} f(x) dx = \lim_{n \to \infty} \sum_{k=0}^{n} f(a+ \frac{b-a}{n} k) \frac{b-a}{n} \]

에서 \( f(x) = \ln(x) \)일때 구간의 분할 간격을 나타내는 \( \frac{b-a}{n} \)을 \( 1\)로 바꿔 상황에 맞도록 근사하자.

\[ \int_{a}^{n+a} \ln x dx \approx \sum_{k=0}^{n} \ln(a+ k) \]

\( a=1\) 인 상황에서 \( n+1\) 을 다시 \(n\)으로 바꾼다.

\[ \int_{1}^{n} \ln x dx \approx \sum_{k=1}^{n} \ln(k) \]

이 근사에서 아이디어를 얻는다.

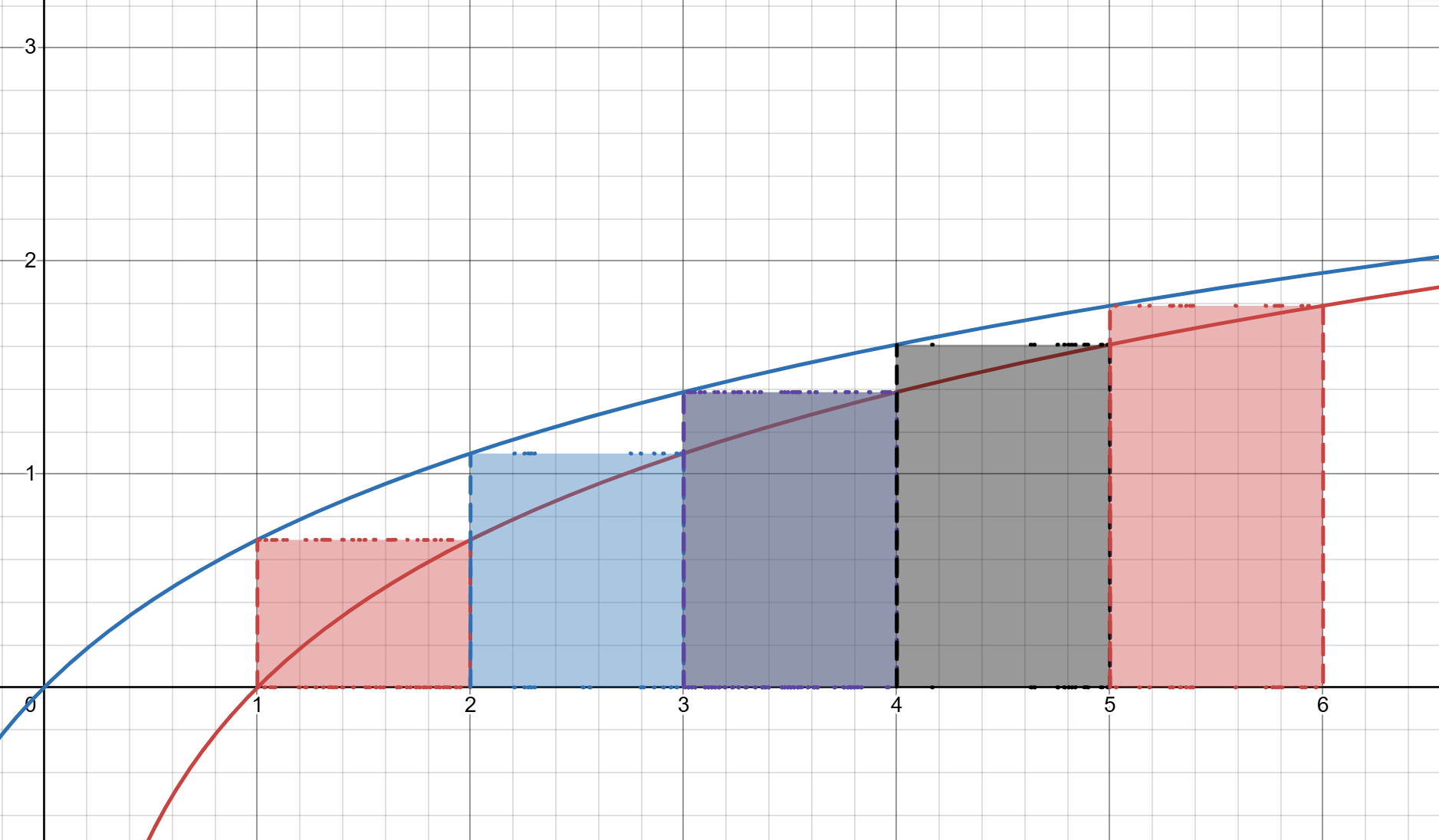
Desmos를 잘 못 써 그림이 좀 더럽다.

해당 근사를 바로 사용하기에는

\[ \ln n - \int_{n-1}^{n} \ln x dx \]

의 오차(위 사각형 중 빨간 곡선 위에 있는 부분)이 조금 거슬릴 수 있다.

이를 방지하기 위해 \( y= \ln(x+1) \)의 그래프를 활용한다.

\[ \lim_{x \to \infty} \left( \frac{d^2}{dx^2} \ln x = - \frac{1}{x^2} \right) =0\]

이므로 \( y=\ln x \)의 그래프는 결국 직선으로 근사된다.

즉, 큰 자연수 \( n\)에 대해 \( \{(x, \, y) \vert \, n \le x \le n+1 \, , \, \ln x \le y \le \ln (n+1) \} \) 의 넓이는 평행사변형으로 근사되는 \( \{(x, \, y) \vert \, n \le x \le n+1 \, , \, \ln x \le y \le \ln (x+1) \} \)의 넓이를 이등분한다고 계산한다.

즉, \( \ln n! \)은 \( \int_{1}^{n} \ln x \, dx \) 와 \( \int_{1}^{n} \ln (x+1) \, dx \)의 산술 평균으로 계산한다. 적분을 계산하면

\[ \ln n! \approx \left( n + \frac{1}{2} \right) \ln n -n +a \]

이때 a는 초반에 두드러지는 선형적인 오차를 나타낸다. 현재 우리는 \( \ln n! \)의 근사를 계산하고 있다. 따라서 이의 선형적인 오차는 \( n! \) 의 비율적 오차를 발생시킨다. 비율 근사를 위해서는 이를 고려해야 한다.

일단 식을 \( n! \) 에 대해 정리하고 보기 좋게 바꾸면 상수 c에 대해

\[ n! \approx c \sqrt{n} \left(\frac{n}{e}\right)^n \]

이다.

c의 값을 구하기 위해서는 팩토리얼이 들어간 비율의 극한 식을 활용하면 된다. 이 글에서는 Wallis' formula를 사용하겠다. 증명이 어마어마하게 다양하다.

\[ \prod_{n=1}^{\infty} \frac {(2n) \cdot (2n)}{(2n-1) \cdot (2n+1)} = \frac{\pi}{2} \]

루트를 씌우고 곱하는 개수가 무한대로 가지 않고 충분히 큰 상황을 가정하면

\[ \prod \frac {2n}{\sqrt{(2n-1) \cdot (2n+1)}} \approx \sqrt{\frac{\pi}{2}} \]

이때 첫 \( (2n-1)\)은 1이고, 마지막 \( (2n+1) \)은 따로 생각한다.

\[ \frac {\prod_{k=1}^{n} (2k)}{\sqrt{2n+1} \prod_{k=1}^{n} (2k-1)} \approx \sqrt{\frac{\pi}{2}} \]

\( \prod_{k=1}^{n} (2k) = 2^n n! \) 이고 \( \prod_{k=1}^{n} (2k-1) = \frac{(2n)!}{2^n n!} \) 이므로 \( n! \approx c \sqrt{n} \left(\frac{n}{e}\right)^n \) 를 대입하면,

\[ \frac{c}{2} = \sqrt{\frac{\pi}{2}} \]

즉,

\[c = \sqrt{2\pi} \]

따라서 증명이 완성되었다.

\[ n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n \]

Conclusion

스털링 근사는 물리에서도 많이 사용되고 많은 분야에서 유용하게 쓰이는 굉장히 유명한 근사이므로 잘 알아두도록 하자.