시간복잡도
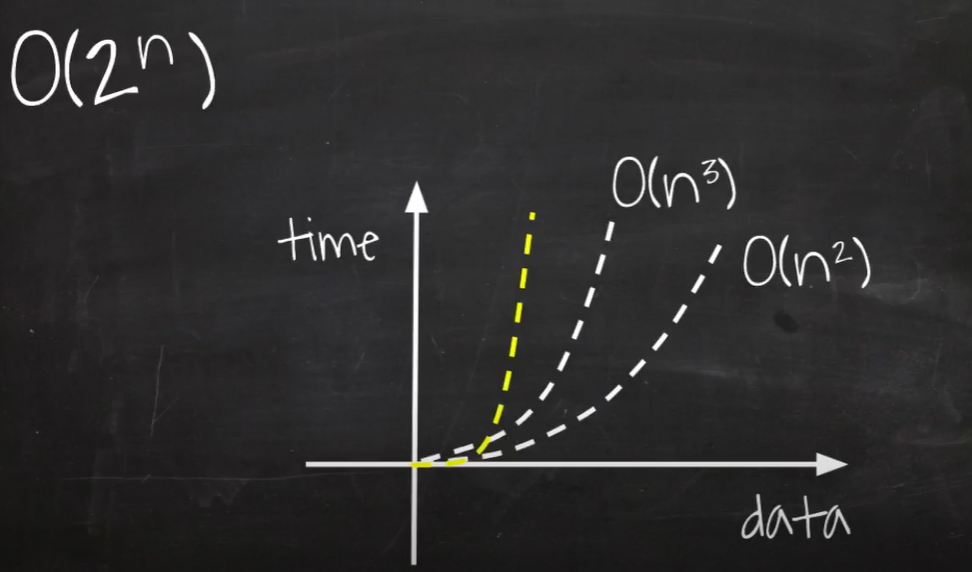
백준같은 곳에서 알고리즘을 공부하다 보면 필연적으로 시간복잡도라는 개념을 한 번쯤은 보게 된다. 단순히 어떤 알고리즘의 시간복잡도가 \(\mathcal{O}(n^2)\)라는 것을 입력의 크기가 \(n\)일 때 최악의 경우에 실행 시간이 \(n^2\)에 비례한다는 것만 알아도 알고리즘 문제를 푸는 것에는 큰 영향이 없지만, 이 글에서는 시간복잡도의 수학적 정의에 대해서 알아보고자 한다.
시간복잡도를 나타내는 방법은 Big \(\mathcal{O}\), Big \(\theta\), Big \(\Omega\)로 크게 3가지가 있다.
Big $\mathcal{O}$
\[\text{어떤 양의 상수 } M, c\text{과 } M \text{이상의 모든 } x\text{에 대해 } \vert f(x)\vert \le c\vert g(x)\vert\text{일 때 } f(x)\in \mathcal{O}(g(x))\]
보통 위의 정의를 만족할 때 이해하기 쉽도록 \(f(x)=\mathcal{O}(g(x))\)라고 표기하는 경우도 있지만, 여기서는 좀 더 엄밀하게 하기 위해 \(f(x) \in \mathcal{O}(g(x))\)로 표기하도록 하겠다.
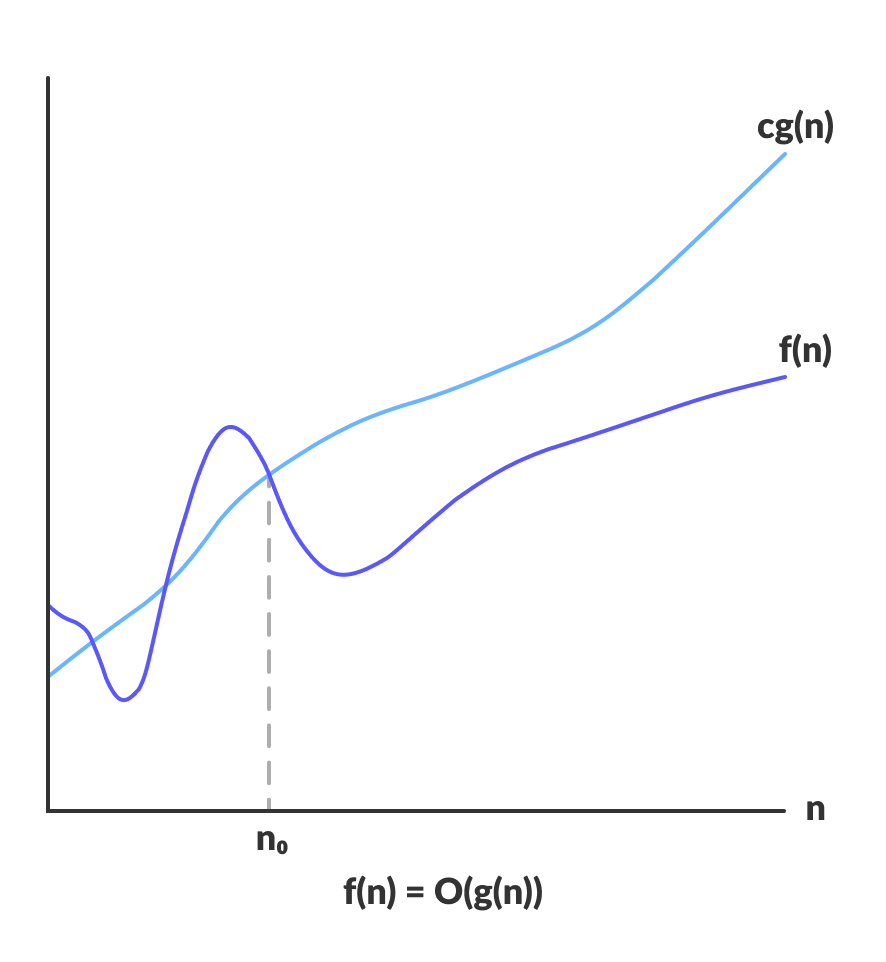
위 그림에서 보면, \(n\)이 \(n_0\)보다 큰 모든 경우에 \(\vert f(n)\vert \le c\vert g(n)\vert\)이므로 \(f(n) \in \mathcal{O}(g(n))\) 이다.
예를 들어 \(f(x) = x^2\)라고 하자.
만약 \(g(x) = x^3\)이라면 \(c\)가 어떤 양수가 되더라도 충분히 큰 \(M\)가 있어 모든 \(M\)보다 큰 \(x\)에 대해 \(f(x) \le cg(x)\)이므로 \(f(x) \in \mathcal{O}(g(x))\)이다.
만약 \(g(x) = x^2 - 3x\)이라면 \(c\)가 모든 양수는 아니더라도 충분히 큰 \(c, M\)이 있어 \(M\)보다 큰 모든 \(x\)에 대해 \(f(x) \le cg(x)\)이므로 \(f(x) \in \mathcal{O}(g(x))\)이다.
하지만 \(g(x) = x\)이라면 \(c\)가 어떤 수가 되더라도 충분히 큰 \(x\)에 대해 \(f(x) > cg(x)\)이므로 \(f(x) \notin \mathcal{O}(g(x))\)이다.
Big $ \Omega $
\[\text{어떤 양의 상수 } M, c\text{과 } M \text{이상의 모든 } x\text{에 대해 } \vert f(x)\vert \ge cg(x)\text{일 때 } f(x)\in \Omega(g(x))\]
즉, \(Big \mathcal{O}\)와 반대라고 생각하면 편하다.
이번에도 예를 들어 \(f(x) = x^2\)라고 하자.
만약 \(g(x) = x^3\)이라면 \(c\)가 어떤 양수가 되더라도 충분히 큰 \(x\)에 대해 \(\vert f(x)\vert < c\vert g(x)\vert\)이므로 \(f(x) \notin \Omega(g(x))\)이다.
만약 \(g(x) = x^2 - 3x\)이라면 \(c\)가 모든 양수는 아니더라도 충분히 작은 \(c\)와 충분히 큰 \(M\)가 있어 \(M\)보다 큰 모든 \(x\)에 대해 \(\vert f(x)\vert \ge c\vert g(x)\vert\)이므로 \(f(x) \in \Omega(g(x))\)이다.
그리고 \(g(x) = x\)이라면 충분히 큰 \(M\)이 있고 \(c\)가 어떤 양수가 되더라도 충분히 큰 \(x\)에 대해 \(\vert f(x)\vert \ge c\vert g(x)\vert\)이므로 \(f(x) \in \Omega(g(x))\)이다.
Big $\theta$
\[f(x) \in \mathcal{O}(g(x)) \text{이고 } f(x) \in \Omega(g(x)) \text{일 때 } f(x) \in \theta(g(x))\]
사실 Big \(\theta\)는 이게 끝이다.
성질
Big \(\mathcal{O}\), Big \(\Omega\), Big \(\theta\) 표기법에는 여러 성질들이 있다.
1. 반사성
\[f(x) \in \mathcal{O}(f(x)), f(x) \in \Omega(f(x)), f(x) \in \theta(f(x))\]
2. 전이성
\[f(x) \in \mathcal{O}(g(x)), g(x) \in \mathcal{O}(h(x)) \text{이면 } f(x) \in \mathcal{O}(h(x))\]
\[f(x) \in \Omega(g(x)), g(x) \in \Omega(h(x)) \text{이면 } f(x) \in \Omega(h(x))\]
\[f(x) \in \theta(g(x)), g(x) \in \theta(h(x)) \text{이면 } f(x) \in \theta(h(x))\]
3. 대칭성
\[f(x) \in \theta(g(x)) \Leftrightarrow g(x) \in \theta(f(x))\]
4. 전치 대칭성
\[f(x) \in \mathcal{O}(g(x)) \Leftrightarrow g(x) \in \Omega(f(x))\]
5. 덧셈 규칙
위에서 추측할 수 있듯이, \(\mathcal{O}(f(x)), \Omega(f(x)), \theta(f(x))\)는 전부 다 집합이다.
\[\mathcal{O}(f(x)) + \mathcal{O}(g(x)) = \mathcal{O}(f(x) + g(x))\]
\[\Omega(f(x)) + \Omega(g(x)) = \Omega(f(x) + g(x))\]
\[\theta(f(x)) + \theta(g(x)) = \theta(f(x) + g(x))\]
예를 들어 \(\mathcal{O}(x^2) + \mathcal{O}(x) = \mathcal{O}(x^2+x) \text{이고, } \mathcal{O}(x^2+x) = \mathcal{O}(x^2)\)이므로 \(x\)가 충분히 큰 수라고 생각했을 때
\[\mathcal{O}(f(x)) + \mathcal{O}(g(x)) = \mathcal{O}(max(f(x), g(x)))\]
으로 써도 무방하다. 마찬가지로
\[\Omega(f(x)) + \Omega(g(x)) = \Omega(min(f(x), g(x)))\]
도 성립한다.
6. 곱셈 규칙
\[\mathcal{O}(f(x)) \cdot \mathcal{O}(g(x)) = \mathcal{O}(f(x) \cdot g(x))\]
\[\Omega(f(x)) \cdot \Omega(g(x)) = \Omega(f(x) \cdot g(x))\]
\[\theta(f(x)) \cdot \theta(g(x)) = \theta(f(x) \cdot g(x))\]
\(f(x) = x^2, g(x) = log(x)\)라 하자. \(x\)가 충분히 클 때 \(\mathcal{O}(f(x))\)에 속한 함수는 \(f(x)\)보다 작거나 같고, \(\mathcal{O}(g(x))\)에 속하는 함수는 \(g(x)\)보다 작거나 같다. 당연히 이 둘의 곱은 \(\mathcal{O}(f(x) \cdot g(x))\)보다 작거나 같다.
어떤 알고리즘이 좋을까?
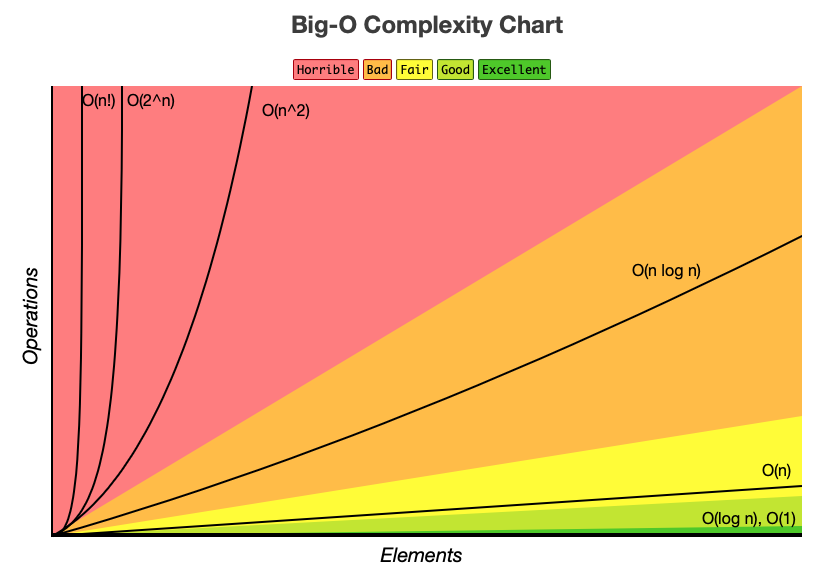
잠시 정보과학의 영역으로 넘어와 보자. 알고리즘의 시간복잡도는 알고리즘의 효율성을 따질 때 중요한 지표 중 하나인데, 맨 처음에도 말했듯이 Big \(\mathcal{O}\) 표기법으로 나타낼 수 있다. \(0 < a < b\)인 \(a, b\)가 존재하고 \(x\)가 충분히 클 때, 알고리즘의 시간복잡도 별 걸리는 시간은 아래와 같다.
\[\mathcal{O}(1) < \mathcal{O}((log(x))^a) < \mathcal{O}((log(x))^b) < \mathcal{O}(x^a) < \mathcal{O}(x^b) < \mathcal{O}(a^x) < \mathcal{O}(b^x) < \mathcal{O}(x!)\]
위의 부등식들과 덧셈 규칙, 곱셈 규칙을 잘 결합하면 알고리즘이 얼마나 효율적인 것인지 알 수 있을 것이다.
결론
처음에는 수학적으로 엄밀하게 시간복잡도를 정의하고 그의 성질들도 엄밀하게 설명하려 했지만, 글을 써내려 갈수록 어쩔 수 없이 직관을 요하는 부분이 많았던 것도 사실이다. 이 점은 독자의 양해를 바란다. 이 글을 다 읽었다면 앞으로는 Big \(\mathcal{O}\) 표기법이 나와도 두려워 할 것 없다. 그러니 여러 알고리즘들을 배울 때 시간복잡도 표기가 나오면 위의 정의와 성질들을 곱씹으며 그것이 무엇을 의미하는지 확실히 이해하기를 바란다.





Comments ()