Introduction

소인수분해. 개념만 들어서는 중학교 1학년때 잠시 배우고 지나간, 굳이 수학의 길로 들어서지 않는다면 영원히 모르고 살아도 될 것 같은 느낌이 드는 개념이다. 혹여나 이런 생각을 하는 독자가 있다면, 이번 글을 읽고나서는 이것에 약간의 흥미를 느낄지도 모르겠다.

자, 내가 지금부터 매우 간단한 과제를 하나 주겠다. 시간제한은 없으니, 아래 수를 소인수분해해보아라. TMI를 달자면 이 수는 8번째 페르마 수이다.

115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,03,457,584,007,913,129,639,937

무운을 빈다. 참고로 정답을 알려주자면 아래 두 수로 소인수분해된다.

• 1238926361552897
• 93461639715357977769163558199606896584051237541638188580280321
• (아 물론 이건 알고리즘을 위한 빌드업이지 필자가 이 해괴망측한 수들을 직접 구한 것은 아니라는 점을 미리 밝힌다.)

내가 찍신도 아니고, 초능력자도 아닌데, 저 숫자들은 도대체 어떻게 얻어낸 걸까? 사실 일종의 찍신이 강림하였다고 할 수도 있겠다. 오늘 알아볼 것은 Pollard's Rho 알고리즘이다.

Before We Begin...

표면상으로 봐서는 Pollard's Rho 알고리즘은 알고리즘이라는 허울을 뒤집어쓴 서커스처럼 보인다. 몇가지 대놓고 이상한 점만 짚어보자면,

• 코드 내부에서 랜덤 함수가 있다. 코딩을 조금만 해본 사람이라면 이게 뭔 어이없는 이야기인지 체감이 될 것이다.
• 함수에 같은 값을 넣어도, 다른 값이 튀어나온다.
  • 사실 이건 어찌 보면 위 랜덤의 특성이라고도 할 수 있겠다.
• 함수 내부에서 자기 자신을 변화 없이 그대로 호출한다. 그러니까 pollardRho(n, v)를 받아서 내부에서 pollardRho(n, v)를 그대로 호출한다.

단순히 봐서는 우리가 아는 모든 코딩의 상식들을 벗어나는, 이상한 알고리즘 같다. 하지만 여기에는 나름대로의 미학이 숨어있다.

그럼, 시작하자.

Overview

일단 필자의 대부분의 글이 그렇듯, 먼저 알고리즘의 전체적인 진행 방식에 대하여 알아보고 시작하자.

일단 파라미터 부터 알아보자. n은 현재 소인수분해하려는 수이다. 이는 제귀적으로 감소한다. set / vector &v는 소인수들을 담을 배열이다. 이것은 결과값용 배열이여서, 소인수를 전부 구하고 싶은지, 아니면 소인수의 종류만 구하고 싶은지에 따라서 적절히 끼우면 된다.

이제 알고리즘을 알아보자.

• \(n=1\)이면 그냥 리턴한다.
• \(n=2k\)이면 \(2\)를 \(v\)에 넣고 리턴한다.
• \(n\)이 소수면 \(n\)을 \(v\)에 넣고 리턴한다.
• \(x=y\), \(c\) 3개의 변수를 묶인대로 랜덤을 설정해준다.
• \(f(x) = x^2+c mod n\)으로 정의하자. 반복문을 돌면서 \(x\)는 \(f(x\)로, \(y\)는 \(f(f(y))\)로 진전시킨다. 이것을 영어로 Tortise Move, Hare Move라고 한다.
• \(|x-y|\)와 \(n\)의 최대공약수를 조사한다.
  • 만일 \(1\)이라면 반복문을 한번 더 돈다.
  • 만일 \(n\)이라면 pollardRho 함수를 받은 파라미터 그대로 재호출한다.
  • 만일 \(n\), \(1\)이 아니라면 그 수를 \(d\)라 하자. pollardRho 함수를 \(d\), \(n/d\)로 재호출한다.

끝이다. 생각보다 간단하지 않은가? 더 궁금한 사람을 위해 아래에 간단한 코드를 첨부한다. 여기서 millerRabin 함수는 단순히 소수인지 아닌지 true/false를 리턴하는 함수이다.

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <vector>
#include <algorithm>
#include <numeric>
#include <set>
using namespace std;
typedef long long int lli;

lli mul(lli a, lli b, lli n) {
    return (__int128)a*b % n;
}

lli power(lli a, lli d, lli n) {
    lli res = 1;
    a %= n;
    while (d > 0) {
        if (d % 2 == 1) {
            res = mul(res, a, n);
        }
        a = mul(a, a, n);
        d /= 2;
    }
    return res;
}

void pollardRho(lli n, set<lli> &v) {
    if(n==1) {
        return;
    }
    if(n%2==0) {
        v.insert(2);
        pollardRho(n/2, v);
        return;
    }
    if(millerRabin(n)) {
        v.insert(n);
        return;
    }
    lli x = (rand()%(n-2))+2;
    lli y = x;
    lli c = (rand()%(n-1))+1;
    lli d = 1;
    while(d==1) {
        x = (power(x, 2, n) + c)%n;
        y = (power(y, 2, n) + c)%n;
        y = (power(y, 2, n) + c)%n;
        d = gcd(abs(x-y), n);
        if(d==n) {
            pollardRho(n, v);
            return;
        }
    }
    pollardRho(n/d, v);
    pollardRho(d, v);
    return;
}

How It Works

그래서, 이건 어떻게 작동하는 걸까. 앞에 단계들은 간단한 예외처리니까 넘어가고, 본격적인 반복문부터 살펴보자.

우리가 이 글(알고리즘)에서 가장 중요하게 다룰 수열이 두가지가 있다. 각각 :
\[ x_k = f(x_{k-1}) \mod{n} \text{, where }f(x) = x^2 + c\]

\[y_{\{p | n,k\}} = x_k \mod{p}\]

여기서 \(f(x)\)의 초기 시작값과 \(c\)는 완전히 랜덤으로 정해진다. (참고로 우리는 프로그램에서 \(p\)를 구하는 것이 목적이다. 즉 \(p\)를 모른다. 모르는 수열을 활용한다니, 재미있지 않은가?)

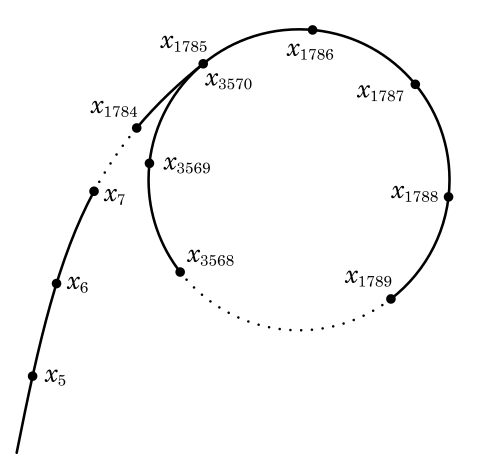
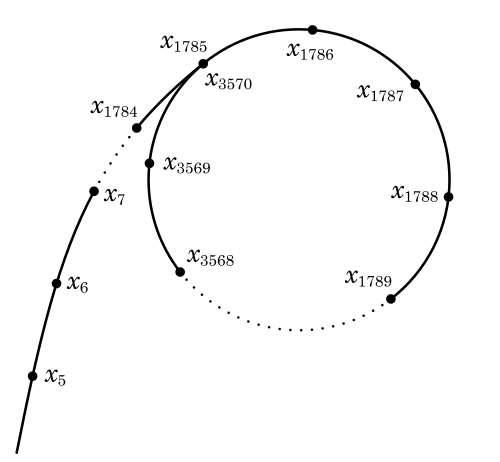
자, 이때 생각해보자. 비둘기집의 원리에 의해 \(x_k\)와 \(y_{\{p,k\}}\)는 각각 \(n\)과 \(k\)내부에서 반복되므로 사이클을 형성할 것이다. 만일 \(x_a \neq x_b\)이면서 \(y_{\{p,a\}} \equiv y_{\{p,b\}}\)인 케이스를 찾게 된다면, \(|x_a - x_b|\)가 \(n\)보다 작은, \(n\)의 인수 \(p\)의 배수가 될 것이다. 즉 \(n\)과의 Greatest Common Divisor를 구해보면 \(p\)를 구할수 있는 것이 된다.

여담으로 이 알고리즘 이름의 Rho는 실제 그리스 문자 Rho를 의미한다. 위 과정을 무한히 실행해보면 아래와 같은 Rho 형태의 그래프가 나오기 때문이다.

Example Problem

13926번: gcd(n, k) = 1

Baekjoon Online Judge스타트링크 (Startlink)

얼핏 봐서는 매우 간단해 보이는 문제이다. RSA 글의 Euler's Totient Function에 관한 설명, 그리고 앞서 말한 Miller-Rabin 소수 판별법을 적절히 섞어 이용한다면 단시간에 해결 가능한 문제이다(심지어 다이아몬드이다!).

정답 코드는 여기서 확인 가능하다.

Conclusion

이 글이 소인수분해, 인수분해, 소수판별법과 관련된 짧은 시리즈의 마지막 글이 될 예정이다. 크게 다루었던 Miller-Rabin 소수판별법과 Pollard's Rho 알고리즘 모두 얼핏 봐서는 이상한 괴리감들이 존재하지만, 그것들을 적절히 조정함으로써 범위 내에서는 문제가 없는, 일명 실용적 알고리즘의 형태를 띄는 것이다.