RSA, and Bézout's Numbers
Introduction
최근 인터넷을 돌아다니다 보면 이런 뉴스를 심심찮게 볼수 있다
RSA는 뭐고, 이건 양자컴퓨터랑 무슨 관련이 있는 것일까? 양자컴퓨터 부분은 담에 알아보고, 우선은 RSA가 뭔지, 이것은 어떻게 작동하는지를 알아보고 증명해보자.
암호화의 기본 원리
내가 10m 떨어진 친구한테 abcd라는 비밀, 즉 Secret를 전해야 한다고 생각하자. 그냥 말하면 주위의 모든 사람들이 비밀을 알게 될 것이다. 당연히 이러면 망한다.
이에 대응하기 위해 우리는 암호화를 사용할 수 있다. 본인이 무엇으로 암호화할지 말하고, abcd를 그 방법으로 암호화한 것을 보내는 식이다. 이는 종류가 2가지가 있는데, Hashing이라고도 알려진 단방향 암호화와 양방향 암호화가 그것이다.
단방향 암호화의 경우, 처음의 방법만을 가지고는 원래의 abcd를 복원하지 못하는 경우이다. 이 경우 나와 내 친구 둘 사이의 제3자가 암호화 방법만을 가지고는 원래 식을 유추 못한다는 장점이 있지만, 반대로 말하면 친구도 이것을 해독하지 못하므로 무용지물이다.
양방향 암호화는 처음의 방법을 적절히 활용해 원래 식을 알아낼 수 있는 경우이다. 이 경우 친구는 이것을 해석할 수 있지만, 주위의 사람들도 우리의 비밀을 알 수 있게 된다.
이처럼 우리가 간단하게 생각해볼수 있는 암호화는 이런저런 문제가 존재한다. 이를 해결하기 위해 초기의 컴퓨터 과학자들이 고안해낸 위대한 알고리즘이 RSA 알고리즘이다.
What is RSA?
RSA는 창시자인 Ron Rivest, Adi Shamir, Leonard Adleman의 성을 각각 가져와 붙은 이름이다. 간단히 개념만 설명하자면, 이는 Private Key와 Public Key를 이용하여 Public Key를 가지고서는 암호화만 가능하고, Private Key를 이용해야지만 복호화가 가능한 암호 체계이다.
알고리즘의 작동을 설명하기 전에, 증명해야 하는 것들이 좀 있고, 알아봐야 하는 개념들도 여럿 있다. 과장 안하고, 매우 많다. 그럼 알아보자.
Appetizer
New Terms
- 이 글에서는 Totient Set \(S\)와 \(\phi(n)\), 즉 Euler's Totient Function이 매우 자주 사용된다. 만일 \(\phi\) 혹은 \(\phi(n)\)를 보게 된다면 이는 위 함수를 의미한다.
- 잘 모르는 독자들을 위해 잠시 설명하자면, \(\phi (n)\)은 \(n\)보다 작으면서 \(n\)과 서로소인 집합, 즉 Totient Set \(S\)의 크기를 의미한다.
- 즉, \(S\) 를 수학적으로 정의하자면 \(S = \{1 \leq x \leq n | gcd(x, n) = 1 \}\)이 되고, \(n(S) = \phi (n)\)를 만족한다.
- Bézout's Number란, 숫자 \({a,b}\)에 대하여 \(ax + by = 1\)라는 식을 만족하는 정수 숫자 \({x,y}\)를 의미한다. 이때, Bézout's Identity으로부터 \(gcd(a,b) = 1\)일 경우 \({x,y}\)가 존재함이 밝혀져 있다. 자세한 내용은 이 글을 참고바란다.
Proofs
CLAIM 1 : EULER'S TOTIENT FUCTION(1)
\[\phi (n) = (p-1)(q-1)\]
첫 증명이라 그런지 증명 자체는 간단하다. \(p\)가 소수이므로 \(\phi (n)\)을 구하는 과정에서 \({1, 2, \cdot \cdot \cdot n-1}\)에서 \(p\)개의 수마다 \(1\)개의 수가 빠짐을 알 수 있다. 또한, \(q\)에 대해서도 비슷하게 성립한다. 따라서, \(\phi (n)\)의 식은 다음과 같이 정의된다 :
\[\phi (n) = n \cdot \frac{p-1}{p} \cdot \frac{q-1}{q} \]
여기서 \(n=pq\)인 사실을 이용하면 :
\[\phi (n) = (p-1) \cdot (q-1)\]
CLAIM 2 : BÉZOUT'S IDENTITY & CODE
우선 우리는 이 증명을 위해서 Bézout's Identity을 알아야 한다. 위에서도 설명한 것 처럼, 이것은 숫자 \({a,b}\)에 대하여 \(ax + by = gcd(a,b)\)라는 식을 만족하는 정수 숫자 \({x,y}\)가 항상 존재한다는 것을 의미한다. 우리는 이 특수해를 코드를 통해 찾아볼 것이다.
이 증명은 증명이라기 보다는 코드를 구현해야 하는 문제이다. 일반적으로 코딩할때의 GCD 함수를 기억하는가? 아마 대부분의 경우 이것을 유클리드 호제법으로 구현하였을 것이다. 하지만 우리는 이제 Bézout's Number를 구해야 한다. 이를 위하여 확장된 유클리드 호제법, 혹은 Extended Eucledian Algorithm을 이용하자.
유클리드 호제법을 전개해나가다 보면 다음과 같은 식의 형태를 볼 수 있다.
\[ a_n = b_n \cdot q_n + r_n \cdot \cdot \cdot \raisebox{.5pt}{\textcircled{\raisebox{-.9pt} {1}}}\]
유클리드 호제법의 정의에 의해 다음 단계에서는 \(a_{n+1} = b_n\), \(b_{n+1} = r_n\)임을 알 수 있다. 이때 우리는
\[ a_{n+1} \cdot x_1 + b_{n+1} \cdot y_1 = 1 \cdot \cdot \cdot \raisebox{.5pt}{\textcircled{\raisebox{-.9pt} {2}}}\]
을 만족하는 해 \( \{x_1, y_1\} \)을 재귀적으로 받았다고 가정할 수 있다. \(\raisebox{.5pt}{\textcircled{\raisebox{-.9pt} {1}}}\)을 \(r_n\)에 대하여 정리하면
\[r_n = a_n - b_n \cdot q_n\]
임을 알 수 있고, 이를 \(\raisebox{.5pt}{\textcircled{\raisebox{-.9pt} {2}}}\)에 대입 후 정리시
\[ a_n \cdot \{y_1\} + b_n \cdot \{ x_1 - q_n \cdot y_1\} = 1\]
이 성립한다. 따라서 이 함수의 리턴값은 \( \{y_1, x_1 - q_n\cdot y_1\}\)이 될 것이다.
이 알고리즘을 코드로 그대로 구현한다면 다음과 같이 구현할 수 있다. 이 함수는 Bézout's Identity의 특수해를 구하는 함수이고, 만약 \(a\)와 \(b\)가 서로소가 아닐 경우 작동을 중지하게 설계되어 있다. C++17 이후라면 optional을 써서 더 깔끔하게 구현할 수 있다.
#include <stdio.h>
#include <vector>
using namespace std;
pair<int,int> getBezoutNumbers(int a, int b) {
if(b==0) {
if(a==1) {
return make_pair(1,0);
} else {
return make_pair(0,0);
}
}
pair<int,int> result = getBezoutNumbers(b, a%b);
if(result==make_pair(0,0)) {
return result;
} else {
return make_pair(result.second, result.first - a/b * result.second);
}
}
int main(void){
int a = 0;
int b = 0;
scanf("%d %d",&a, &b);
printf("%d %d", getBezoutNumbers(a, b).first, getBezoutNumbers(a, b).second);
}
CLAIM 3 : EULER'S TOTIENT FUNCTION(2) & SET
\[let \space S = \{1 \leq x \leq n \space |\space gcd(x, n) = 1 \}\]
\[then \space ^{\forall} a \in S, \\^{\exists} a^{-1} \in S \space s.t. \space aa^{-1} \equiv 1 \space mod \space n\]
이것을 증명하기 위해 CLAIM 2의 Bézout's Identity를 이용하자. \(a\)는 \(S\)에 속해있으므로 \(gcd(a, n) = 1\)이 성립한다. 즉, Bézout's Identity의 \(a\), \(b\)의 후보군의 조건을 만족한다는 것이다. 그리하여 다음과 같은 식을 세울 수 있다 :
\[ a\cdot x + n\cdot y = 1\]
여기서 주의해야 하는 점은 \(x\)가 여러개 있을 수 있다는 것이다. Bézout's Identity를 만족하는 어느 한 특수해를 \( x', y'\)라 하고 디오판토스 부정방정식의 일반해 해법을 이용시, \(x = x' + kn\)가 나오게 된다.
양변의 modulo n을 취하게 된다면
\[ a \cdot x \equiv 1 \space mod \space n\]
가 된다. 앞서 우리가 구해놓은 \(x\)의 일반항은 modulo n에 대하여 항상 같은 값을 가지게 된다. 또한, 일반항의 형태가 \(x = x' + kn\)이므로 \(0 \lt x \leq n\)의 범위에서는 정확히 한개의 해가 존재할 것이다. 이 식의 형태로부터 \(x\)는 \(a\)의 역원이고, 여기서 \(x\)와 \(a\)가 대칭성을 띄기 때문에 \(x\)와 \(a\)가 서로 역원 관계이며 둘다 \(S\) 내부에 존재함을 알 수 있다.
따라서, Euler's Set \(S\) 내부의 모든 원소는 modulo n에 대한 역원이 \(S\)에 존재함을 알 수 있다.
CLAIM 4 : BIJECTIVITY
아마 이 글을 읽는 대부분의 독자들은 수업시간에 배웠겠지만, 잠시 단사성과 전사성의 정의를 복습하고 넘어가자.
전사성이란, 공역의 모든 원소 y에 대하여 대응되는 x의 값이 존재하는 상태를 의미한다. 수학적으로 서술하자면,
\[ ^{\forall} y \in S, \space ^{\exists}x \in S \space s.t.\space f(x) = y \]
또한, 단사성이란 정의역의 한 수 가 공역의 정확히 한 수에만 대응되는 경우를 의미한다. 이 또한 수학적으로 서술하면,
\[ ^{\forall} x_1, x_2 \in S, f(x_1) = f(x_2) \Longrightarrow x_1 = x_2\]
가 될 것이다. 당연히 전단사 함수라면 이것들을 모두 만족해야 할 것이다. 각각을 증명해보자.
i) INJECTIVITY(단사성)
만일 \(f(x_1) = f(x_2)\)라면 \(a \cdot x_1 \equiv a \cdot x_2 \space mod \space n \) 가 성립할 것이다. 이때 \(gcd(a, n) = 1\)이므로 \(a\)의 modulo n의 역원 \(a^{-1}\)이 존재한다. 따라서 이를 양변에 곱해주면 \(x_1 \equiv x_2 \space mod \space n\)이 되는데, \(x_1\)과 \(x_2\)가 정의역인 \(S\)에 속해있으므로 \(\equiv\)를 =로 바꾸어도 문제가 없다. 따라서 \(x_1 = x_2\)이므로 단사성의 증명은 완료하였다.
ii) SURJECTIVITY(전사성)
어떤 \(y \in S\)가 있다고 하자. 우리는 이 \(y\)에 대하여 \(a \cdot x \equiv y \space mod \space n\)인 \(x \in S\)을 찾아야 한다. \(gcd(a, n) = 1\)이므로 \(a^{-1}\)이 존재하므로, \(x \equiv a^{-1} \cdot y \space mod \space n\)이 성립한다. 이때, \( a^{-1}, y \in S\)이므로 \(x \in S\)를 비교적 쉽게 알 수 있다.
CLAIM 5 : EULER'S THEOREM
\[ a^{\phi (n)} \equiv 1 \space mod \space n\]
다음 식을 생각해보자.
\[ \prod_{x \in S} x \cdot \cdot \cdot \textcircled{1}\]
그리고 그것을 이 식과 비교해보자.
\[ \prod_{x \in S} a \cdot x \space where \space a \in S \cdot \cdot \cdot \textcircled{2}\]
CLAIM 4에서 증명했듯, \(f(x) = a \cdot x\space mod \space n\)는 \(S \rightarrow S\)에 대하여 전단사 함수이기에 이 두 식의 값은 modulo n에 대하여 동치일 것이다.
한편, \( \textcircled{2}\) 식을 정리하자면, \(a\)는 \(n(S) = \phi (n)\)만큼 곱해지므로, 이것을 앞으로 묶는다면,
\[ a^{\phi (n)} \cdot\prod_{x \in S} x \space where \space a \in S \cdot \cdot \cdot \textcircled{3}\]
그런데, \( \textcircled{1} \equiv\textcircled{3} \space mod \space n\) 라는 등식에서 \( \textcircled{1}\)에 해당하는 식은 각 요소가 전부 n과 서로소이므로 \( \equiv\) 양변에서 나누어도 된다. 따라서, 우리는 최종 식인
\[ a^{\phi (n)} \equiv 1 \space mod \space n\]
를 얻을 수 있다.
CONCLUSION
워낙 증명이 많았기에 우리가 지금까지 증명했던 것을을 차례대로 나열해보자.
\[\phi (n) = (p-1)(q-1)\]
\[ ^{\forall}x_1, x_2 \in \mathbb{Z}, ^{\exists}a_1, a_2 \in \mathbb{Z} \space s.t. \space x_1 \cdot a_1 + x_2 \cdot a_2 = gcd(x_1, x_2)\]
\[let \space S = \{1 \leq x \lt n \space |\space gcd(x, n) = 1 \}\]
\[then \space ^{\forall} a \in S, \\^{\exists} a^{-1} \in S \space s.t. \space aa^{-1} \equiv 1 \space mod \space n\]
\[ a^{\phi (n)} \equiv 1 \space mod \space n\]
나중에 아래의 최종적인 증명에서 이 CLAIM들이 매우 중요하게 사용되는데, 이것이 무엇이었는지 기억이 안난다면 이곳을 참고하자.
Main Dish : The RSA Encryption Method
Overview
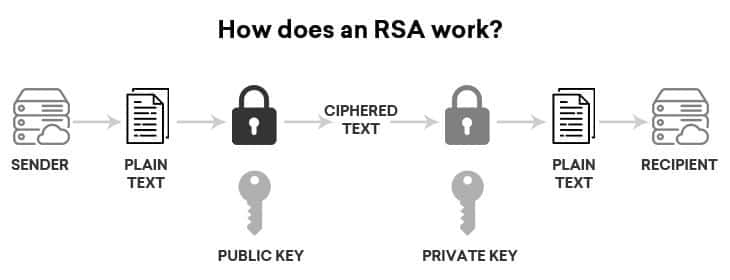
자, 이제 Appetizer가 겨우 끝났다. 지금부터는 실제 RSA 암호체계가 어떻게 전달하는지를 알아보자. 자세한 내막을 알기 전에, 우선 전체적인 진행 과정은 아래와 같다.
- 서버는 클라이언트에게 두개의 숫자로 이루어진 공개키(Public Key) \( \{ n, e\}\)를 전달한다.
- 클라이언트는 어떤 평문 \(m\)을 숫자로 바꾼 후 \( \{ n, e\}\)를 이용하여 암호화 한 후 전달한다. 이 암호문을 \(c\)라 하자.
- 서버에게는 아직 새상에 공개 안한 비밀키(Private Key) \(d\)가 존재한다. 서버는 이제 \( \{ c, n, d\}\)를 이용하여 \(c\)를 \(m\)으로 복호화한다.
처음 듣기에는 매우 난해할 수 있다. 이제 이를 자세히 알아보고, 이런게 왜 작동하는지 알아보자.
Specifics
우선, 서버는 거대한 소수 테이블에서 두개의 소수 \(p\)와 \(q\)를 가져온다. 이 둘을 곱하여 Public Key \(n\)을 만든다. 원래 \(n\)을 소인수분해하여 \(\phi (n)\)를 얻는 것은 매우 힘들지만, CLAIM 1에 따라 서버는 매우 쉽게 \(\phi (n)\)를 알 수 있게 된다. (이것이 RSA 암호화의 가장 중요한 포인트이다.)
또한, 공개키의 다른 부분인 \(e\) 또한 필요하다. \(e\)의 값은 \(\phi(n)\)과 서로소가 되도록 잡아줄 것이다. 우리에게는 위대한 Bézout's Identity가 있으므로 \(e\)의 modulo \(\phi (n)\)에 대한 역원을 쉽게 찾을 수 있다(CLAIM 4의 방법 응용). 이 역원을 \(d\)라 하고, 우리의 Private Key로 삼자.
클라이언트는 서버가 위 과정을 거친 다음 \( \{ n, e\}\)를 전달받는다. 이후, 클라이언트는 자신의 평문 \(m\)를 \(e\)제곱 한 후, modulo n을 취하여 반환한다.
서버는 방금 받아진 정보를 다시 \(d\)제곱한 후, modulo n을 취한다. 이 경우, 매우 신기하게도, 원래 평문 \(m\)을 얻을 수 있다!
How?
앞서서 우리는 \(d\)를 구하기 위하여 Bézout's Identity 를 이용하였다. 그 식을 다시 써보면,
\[ e\cdot d + \phi (n) \cdot k = 1\]
이 성립한다. 여기서 \(k\)는 단순히 어떤 정수이다. 중요하지 않으므로 그냥 넘기자.
이로부터, 우리는 \( m^{e\cdot d}\)가 \( m^{1 - \phi(n) \cdot k}\)임을 알 수 있다. 이때, CLAIM 5의 \(m^{\phi (n)} \equiv 1 \space mod \space n\)로 부터, 위 식의 modulo n을 취한 것에 \(m^{\phi (n)} \)를 \(k\)번 곱하게 되면 단순히 \(m^1 \space mod \space n\)이 됨을 알 수 있다! 안전한 암호화 및 복호화에 성공한 것이다!
잠깐, 아직 기쁘기는 이르다. 우리는 앞서 CLAIM 5가 \(m\)과 \(n\)이 서로소일 경우에 대해서만 증명했었다. 하지만, 이것을 어떻게 보장할 수 있을까? \(m\)은 클라이언트가 자기 마음대로 정하는 평문이다. 서로소라는 보장이 절대 없다. 이를 해결하기 위해서 중국인들의 도움을 잠시 빌리자.
CRT Time
중국인의 나머지 정리를 잠시 이용하자. 초기의 조건에서 우리는 \(n=pq\), 즉 두 개의 소수의 곱으로 정의하였다. 따라서, CLAIM 5의 식을 잠시 각 소인수의 관점에서 확인해보자.
일반성을 잃지 않고 소인수 \(p\)의 관점에서 볼 때, 만일 \(m\)이 \(p\)의 배수가 아니라면 둘이 서로소라는 뜻이고, 이는 이후 CLAIM 5를 이용하여 쉽게 전개 가능하다. 또한, 만일 \(m\)이 \(p\)의 배수라면, \(m^{e\cdot d} \equiv 0 \equiv m \space mod \space p\)이므로, 두가지 케이스 모두에 대하여 \( m^{ed} \equiv m \space mod \space p\)가 성립한다. 같은 논리로, q에 대해서도 동일한 식이 성립한다.
최종적인 결론을 위해 두 식을 합치자. \( m^{ed} \equiv m \space mod \space pq = n\)이 되므로, 앞선 증명에서 필요한 조건은 충족되었다고 할 수 있다.
Conclusion..?
오늘은 현실세계에서 컴퓨터 암호화의 시초라고도 할 수 있는 RSA 암호화 체계에 대하여 알아보았다. RSA는 현재 셀 수도 없이 많은 웹사이트의 표준 보안 방식으로 사용되고 있으며, \(\phi(n)\)의 독특한 특성 덕분에 일반적인 컴퓨터로는 뚫는 것이 불가능한 궁극의 암호체계를 구성하였다.
사실 RSA라는 알고리즘 자체는 매우 오래된 알고리즘이다. 심지어, 원 개발자들에 의해 RSA가 처음 제안된 해는 1977년인데, 이는 사실상 최초의 가정용 컴퓨터인 알테어 8800가 출시된 바로 직후인 만큼 컴퓨터 산업이 그렇게 발전하지 않았던 때이다. 컴퓨터가 제대로 보급되기도 전에, 미래 1세기동안의 정보보안을 책임질 알고리즘을 개발해냈다는 것이, 매우 낭만적이지 않은가?
하지만, 현대에 와서 양자컴퓨터의 등장과 함게 이 위상도 조금씩 흔들리고 있다. 다음 편에서는 양자컴퓨터와 암호체계들의 싸움에 대하여 다뤄보고자 한다.
혹 오늘 글에서 궁금한 점이 생긴 독자들은 아래 첨부한 원논문을 읽어보는 것을 추천한다.





Comments ()