String Matching Algorithms

1.Introduction
"나는 제발 제발 제발 제발 제발 자고 싶다"라는 문장에서 "제발"의 위치를 모두 찾아보자. "나"를 position \(0\)라고 했을때 \(3, 6, 9, 12, 15\)에 있다는 것을 알 수 있다.
위에는 농담이고, 아무튼 위와 같은 작업을 수행하는 것을 String Matching이라고 한다. 세상에는 여러 String Matching 알고리즘이 존재하고, 각각의 목적은 다르다. 이번 글에서는 PS에서 사용되는 여러 종류의 String Matching Algorithm에 대해서 알아보자.
오늘 다룰 알고리즘들은 KMP, Trie, Aho Corasick, 그리고 Rabin Karp 알고리즘이다. 각각의 의도는 다음과 같다.
- KMP : 문자열 \(S\)가 있을 때, 패턴 \(P\)를 찾는 알고리즘
- Trie : 문자열 \(N\)개가 있을 때, 문자열 \(S\)를 찾는 알고리즘
- Aho Corasick : 패턴 \(N\)개가 있을 때, 이를 문자열 \(S\) 속에서 찾는 알고리즘
- Rabin Karp : 문자열 \(S\)가 있을 때, 해시를 이용하여 패턴 \(P\)를 찾는 알고리즘
자, 시작하자.
2.KMP
KMP알고리즘은 PS 중상급을 풀다보면 항상 만나는 중간보스 느낌의 알고리즘이다. 하지만 KMP의 이점을 이해하려면 우선 Naive 알고리즘의 원리를 생각해보자.
Naive한 알고리즘은 대충 아래와 같이 작동한다.
- \(S\)와 \(P\)를 찾는다.
- 시작 인덱스 \(i\)에 대하여 인덱스 \(j\)에서 \(S[j]\)와 \(P[j-i]\)를 비교한다.
- 달라지면 \(i\)를 하나 증가시킨다.
- 완전히 같은 지점을 찾으면 \(i\)를 기록한다.
하지만, 이 알고리즘은 개선의 여지가 있다. 생각해보자. 내가 만약 \(P\)가 "abcabce"이고, \(S\)가 "abcabcabcabce"라고 생각해보자. Position 6에서 불일치 판정이 나지만, 생각해보면 여기서는 우리가 놓친 정보가 있다. "abcabce"에서 "e" 직전에는 "abc"라는 phrase가 반복된다. 따라서 우리는 1칸만 미는 것이 아니라, 3칸씩 한번에 밀 수 있는 것이다.
이처럼 어느 부분 문자열의 접두사와 접미사가 같다는 점을 이용하는 알고리즘이 KMP이고, 이를 위해서 우리는 패턴 \(P\)의 LPS(Longest Proper Prefix which is also a suffix. 줄임말이 왜 저런지는 잠시 넘기도록 하자. 필자는 주로 코딩할때 preprocessing을 이용한다. Fail 함수라는 표현도 이용된다. 으아....)
간단한 KMP의 구현은 아래와 같다.
#include <iostream>
#include <vector>
#include <string>
using namespace std;
// KMP Algorithm
void computeLPS(const string& pattern, vector<int>& lps) {
int length = 0;
lps[0] = 0;
int i = 1;
while (i < pattern.length()) {
if (pattern[i] == pattern[length]) {
length++;
lps[i] = length;
i++;
} else {
if (length != 0) {
length = lps[length - 1];
} else {
lps[i] = 0;
i++;
}
}
}
}
void KMPSearch(const string& text, const string& pattern) {
int n = text.length();
int m = pattern.length();
vector<int> lps(m);
computeLPS(pattern, lps);
int i = 0; // index for text
int j = 0; // index for pattern
while (i < n) {
if (pattern[j] == text[i]) {
i++;
j++;
}
if (j == m) {
cout << "KMP: Found pattern at index " << i - j << endl;
j = lps[j - 1];
} else if (i < n && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
}
int main() {
string text = "AABAACAADAABAAABAA";
string pattern = "AABA";
KMPSearch(text, pattern);
return 0;
}
3.Trie
Trie는 매우 특이한 알고리즘이다. 이름이 Tree와 비슷하니까 그렇게 외워도 좋다. 필자의 지식에 따르면 Trie라는 이름은 ReTRIEval의 대문자된 부분에서 따온 것이다(작명센스..) 앞에서도 말했지만, Trie는 문자열 \(N\)개가 있을 때, 문자열 \(S\)를 찾는 알고리즘이다. 즉, 하나의 사전(Dictionary)인 것이다.
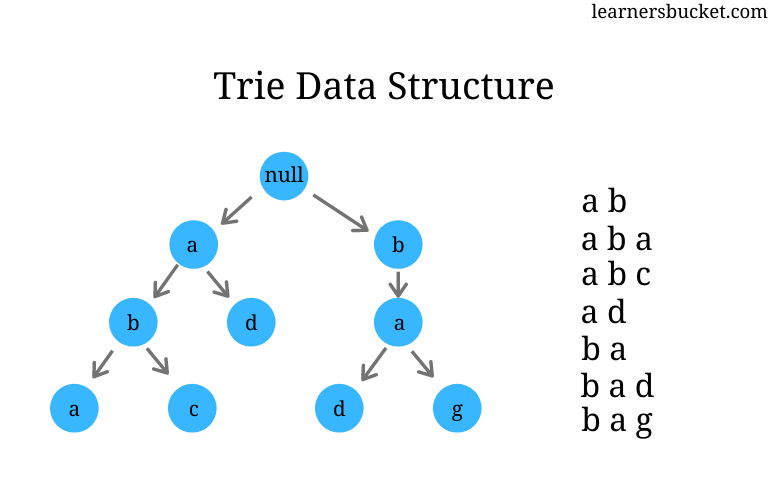
위 그림은 Trie의 형태를 잘 보여준다. 여러 문자열이 들어왔을 때, 여러 문자열들의 같은 접두사들을 묶어 저장하는 형태이다. 이는 아무 랜덤한 문자열이 들어왔을 때, 이것이 존재하는지를 \(O(n)\)만에 찾게 해준다.
Trie를 구현하자면 다음과 같이 할 수 있다 :
#include <iostream>
#include <string>
#include <unordered_map>
using namespace std;
// Trie
struct TrieNode {
unordered_map<char, TrieNode*> children;
bool isEndOfWord;
TrieNode() : isEndOfWord(false) {}
};
class Trie {
public:
TrieNode* root;
Trie() {
root = new TrieNode();
}
void insert(const string& word) {
TrieNode* current = root;
for (char c : word) {
if (current->children.find(c) == current->children.end()) {
current->children[c] = new TrieNode();
}
current = current->children[c];
}
current->isEndOfWord = true;
}
bool search(const string& word) {
TrieNode* current = root;
for (char c : word) {
if (current->children.find(c) == current->children.end()) {
return false;
}
current = current->children[c];
}
return current != nullptr && current->isEndOfWord;
}
};
int main() {
Trie trie;
trie.insert("hello");
trie.insert("world");
cout << "Trie: 'hello' found? " << (trie.search("hello") ? "Yes" : "No") << endl;
cout << "Trie: 'hell' found? " << (trie.search("hell") ? "Yes" : "No") << endl;
return 0;
}
사실 Class와 Struct를 안써서도 구현하는 방법이 존재하지만, 위 코드처럼 깔끔한 Main문을 원한다면 Class를 쓰는 것을 추천한다.
4.Aho Corasick
자....이제부터 슬슬 머리가 아파지기 시작한다. 우리는 지금까지 문자열 \(S\)가 있을 때 패턴 \(P\)를 찾는 알고리즘과 문자열 \(N\)개가 있을 때 문자열 \(S\)를 찾는 알고리즘을 살펴보았다. 그렇다면, 자연스럽게 패턴 \(N\)개가 있을 때 문자열 \(S\) 속에서 이를 찾는 알고리즘도 알아보아야 하지 않겠는가? 이것을 가능하게 해주는 것이 Aho Corasick 알고리즘이다. 거창한 것은 없다. 사실상 Trie에 KMP를 접목시켜 놓은 것이다.
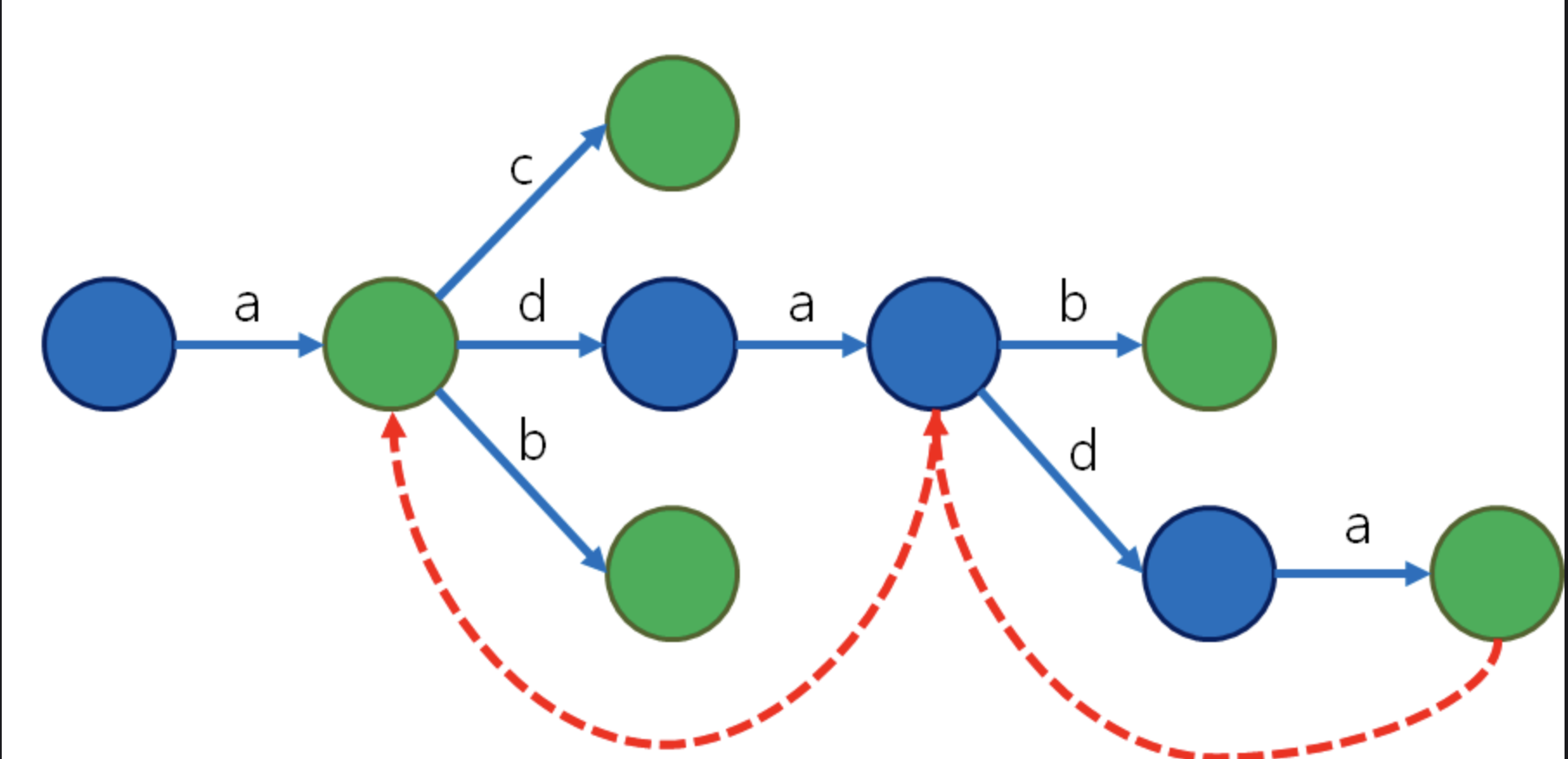
위 그림은 Aho Corasick 전처리 과정에서 생성되는 그래프의 모습이다. 여기서도 Fail 배열이 나오는데(위에서 빨간색 점선 화살표), 이는 KMP처럼 여기서 어긋났을때 갈 수 있는 곳을 저장한다.(아래 코드의 buildFailureLinks 참조) 또 각 node에는 output이라는 이상한 배열이 있는데, 여기에는 내부에 속해 있는 모든 부분 패턴들까지도 저장하기 위해 사용된다. 가령, "aba"내부에는 "ab"가 속하기에 이것을 별도 처리 해줄 필요가 있다.
그래서 아무튼 Aho Corasick 알고리즘은 어떻게 작동하는 걸까? 생각해보자. 내가 어떤 문자열 "......yes......"에서 여러 패턴 중 "yes"를 찾는다고 해보자. 앞에서 어떻게 되었든 yes를 실행시에는 Trie의 Root를 보고 있을 것이고(이건 바로 다음 케이스를 보면 조금 더 이해될 것이다) 여기서부터 "y" "e" "s" 를 순서대로 찾아가면 될 것이다.
하지만 만약 "........eyes....."라는 문자열이 있고, 여기에서 "eyd"와 "yes"를 찾아야 하면 어떻게 할까? 루트에서 바로 찾을 수 있는 "e" "y" 까지 갔다가, "e/d"에서 불일치가 나게 된다. 이 경우 Trie에서 "y->y"로 점프해야지만 "yes"를 찾을 수 있다. 이런 연결들을 만드는 것이 Fail 배열이자 Preprocessing이다.
Aho Corasick 알고리즘의 사기적인 성능은 시간복잡도에서 나온다. 이 모든 패턴들의 위치를 전부 구하는데 \(O(N+M+V)\)밖에 소요되지 않는다. 여기서 \(N\)은 테스트 문자열의 길이, \(M\)는 패턴의 개수, 그리고 \(V\)는 전체 찾은 문자열의 개수에 해당한다. 다른 복잡한 계산은 제쳐두고, 이것을 선형 시간에 계산해낼 수 있다는 것이 놀라운 것이다.
Aho Corasick 알고리즘의 코드는 아래와 같다. 좀 길고, 익숙한 부분들이 중간중간에 보이는데, 이는 이 알고리즘이 KMP, Trie, BFS 등 유명한 알고리즘들을 사용하여 그렇다.
#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
// Aho-Corasick
struct AhoCorasickNode {
unordered_map<char, AhoCorasickNode*> children;
AhoCorasickNode* failureLink;
vector<int> output;
AhoCorasickNode() : failureLink(nullptr) {}
};
class AhoCorasick {
public:
AhoCorasickNode* root;
AhoCorasick() {
root = new AhoCorasickNode();
}
void insert(const string& pattern, int patternIndex) {
AhoCorasickNode* current = root;
for (char c : pattern) {
if (current->children.find(c) == current->children.end()) {
current->children[c] = new AhoCorasickNode();
}
current = current->children[c];
}
current->output.push_back(patternIndex);
}
void buildFailureLinks() {
queue<AhoCorasickNode*> q;
for (auto& pair : root->children) {
pair.second->failureLink = root;
q.push(pair.second);
}
while (!q.empty()) {
AhoCorasickNode* current = q.front();
q.pop();
for (auto& pair : current->children) {
char c = pair.first;
AhoCorasickNode* child = pair.second;
AhoCorasickNode* temp = current->failureLink;
while (temp != nullptr && temp->children.find(c) == temp->children.end()) {
temp = temp->failureLink;
}
child->failureLink = (temp == nullptr) ? root : temp->children[c];
child->output.insert(child->output.end(), child->failureLink->output.begin(), child->failureLink->output.end());
q.push(child);
}
}
}
void search(const string& text, const vector<string>& patterns) {
AhoCorasickNode* current = root;
for (int i = 0; i < text.length(); ++i) {
char c = text[i];
while (current != nullptr && current->children.find(c) == current->children.end()) {
current = current->failureLink;
}
if (current == nullptr) {
current = root;
continue;
}
current = current->children[c];
if (!current->output.empty()) {
for (int patternIndex : current->output) {
cout << "Aho-Corasick: Found pattern '" << patterns[patternIndex] << "' at index " << i - patterns[patternIndex].length() + 1 << endl;
}
}
}
}
};
int main() {
string text = "AABAACAADAABAAABAA";
vector<string> patterns = {"AABA", "ABAA", "ACAAD"};
AhoCorasick ac;
for(int i = 0; i < patterns.size(); ++i) {
ac.insert(patterns[i], i);
}
ac.buildFailureLinks();
ac.search(text, patterns);
return 0;
}
5.Rabin Karp
Rabin Karp 알고리즘은 String Matching 알고리즘에서 약간의 생태계 교란종으로 취급되는 놈이다. 애초에 접근 자체가 다른다. 원리도 간단하다. 주로 KMP라는 중간보스에게 당하고 온 PS 지망생들이 휴식처로 애용하는 알고리즘이다.
Rabin Karp는 String Hashing의 원리를 이용하여 문자열을 검색한다. 생각해보자. 나한테 들어올 문자열이 항상 알파벳 소문자로만 이루어져있다고 보장받을 수 있다 해보자. 그럼 가냥 \(a=0, b=1, c=2....\)이렇게 한 후 \(26\)진법 수를 만들어 버리면 안되는가?
반박하는 사람들은 이렇게 말할 수도 있다. 아니, 만약 문자열 길이가 \(100\)만 되더라도 이미 \(1*26^{100} = 3.1429306416×10^{141}\)아닌가? 세상에는 이정도 수를 저장할 수 있는 컴퓨터는 없을 것이다.
이를 위해 Rabin Karp 알고리즘은 modular를 사용한다. 생각해보자. 내가 만약 저 숫자의 hash값을 \(1000000007\)로 나눈 값을 취했다 하면, 이론상 서로 다른 문자열에 대하여 hash값이 겹칠 확룰은 \( \frac{1}{1000000007}\)일 것이다. 따라서 사실 이정도만 해도 어지간하면 문제가 안된다.
하지만 그래도 겹치는게 문제가 되는 경우가 있다! 이런 경우를 Hash Collision라고 하는데, 실제로 존재하는 현상이다. 이를 위해서 과학자들은 Hash된 값를 다시 hash하는 등 확률을 낮추는 여러 방법을 고안하였는데, 그리 중요하지는 않으므로 기회가 된다면 다음에 이야기하도록 하겠다.
아무튼 Rabin Karp 알고리즘은 이런 hash의 특징을 잘 이용한다. 문자열 \(S\)을 전처리해놓을 경우 구간 \([i,j]\)에 대하여 hash값을 구할 수 있다. 이것이 만일 \(P\)의 hash값과 다르면 보지도 않고 그냥 넘기는 것이다. 이것이 Rabin Karp알고리즘의 성능의 비밀이다.
여기서 Hash Collision을 걱정하는 독자들도 있을 것이다. 하지만 걱정 안해도 되는 것이, 서로 다른 두 문자열이 같은 hash값을 가질 수는 있어도, 서로 같은 두 문자열이 다른 hash값을 가지는것은 수학적으로 불가능하기 때문이다. 따라서 hash값이 같은 경우 확인해주는 간단한 코드만 추가시 알고리즘을 완성할 수 있다. (아래 참조.)
#include <iostream>
#include <string>
#include <vector>
using namespace std;
// Rabin-Karp Algorithm
void rabinKarpSearch(const string& text, const string& pattern, int q) {
int n = text.length();
int m = pattern.length();
int i, j;
int p = 0; // hash value for pattern
int t = 0; // hash value for text
int h = 1;
int d = 256;
for (i = 0; i < m - 1; i++)
h = (h * d) % q;
for (i = 0; i < m; i++) {
p = (d * p + pattern[i]) % q;
t = (d * t + text[i]) % q;
}
for (i = 0; i <= n - m; i++) {
if (p == t) {
for (j = 0; j < m; j++) {
if (text[i + j] != pattern[j])
break;
}
if (j == m)
cout << "Rabin-Karp: Found pattern at index " << i << endl;
}
if (i < n - m) {
t = (d * (t - text[i] * h) + text[i + m]) % q;
if (t < 0)
t = (t + q);
}
}
}
int main() {
string text = "AABAACAADAABAAABAA";
string pattern = "AABA";
rabinKarpSearch(text, pattern, 101);
return 0;
}
Conclusion
자....드디어 PS에서 유명한 String Search Algorithm들에 대하여 알아보았다. 어려운 알고리즘도 있고, 그에 비해 상당히 쉬운 알고리즘도 있으며, 저게 무슨 소린지 된통 모르겠는 알고리즘들도 존재한다. 하지만 String Search 자체가 워낙 많은 분야에서 자잘하게 사용되기 때문에 알아두는 것을 추천한다.





Comments ()