FA-2 푸리에 급수의 소개

앞으로의 푸리에 해석 글들은 Elias M. Stein과 Rami Sakarchi의 [STEIN 푸리에 해석학] 의 내용들에 아주아주 많이 기반을 합니다.

재밌는 내용이 많으니 흥미가 있으시면 꼭 읽어보는 걸 추천 드립니다!

앞선 글에선 푸리에 급수가 무슨 이유로 생겼는지에 대해 알아봤다면, 이제는 정확하게 푸리에 급수가 뭔지, 그리고 푸리에 급수를 어떻게 생각해야 할지에 대해 얘기해보려 합니다.

글을 시작하기에 앞서 푸리에 급수가 어떻게 생겼는지 보고 갑시다!

f가 구간 [a,b]에서 정의된 함수일 때 푸리에 계수(\(a_n\))와 계수를 통해서 표현되는 푸리에 급수는 다음과 같습니다.

$$a_n=\frac{1}{L}\int_{a}^{b}f(x)e^{-2\pi i n x/L}dx \, \, \, \, (L=b-a)$$

$$f(x)=\sum_{n=-\infty}^{\infty}a_ne^{2\pi i n x/L}$$

다들 벡터에 대해서 많이 알 거라고 생각합니다.

벡터를 어떤 기하적 대상에 대응시킨 뒤 선형변환이며 외적이며 내적 등을 해서 그 기하적 대상의 특성을 볼 수도 있고, 벡터들을 기본 단위 느낌의 기저벡터들의 선형결합으로 나타낼 수도 있습니다.

이러한 벡터는 결국 덧셈과 스칼라 곱셈, 그리고 내적이 되는 숫자들의 묶음으로 생각할 수 있습니다. 이런 벡터들을 모아 놓은 벡터들의 집합을 벡터공간 이라고 합니다.

정확한 정의:

사실 내적이 안 돼도 벡터공간이긴 한데, 내적연산을 이용해서 여러가지를 하기 위해선 내적까지 돼야 좋습니다. 벡터공간에 내적이 정의되면 이를 내적공간이라고 합니다.

여기서 complex conjugate연산이 왜 나오냐 할 수 있는데, 통상적으로 우리가 배우는 내적은 실수체 위에서의 벡터공간의 내적입니다. 복소수체 위에서의 벡터공간에서 내적을 하려면 내적이 하는 하나의 중요한 역할을 생각해 봐야합니다.

바로 내적이 벡터의 크기를 정의한다는 점입니다. 벡터는 자기 자신과 내적 했을 때 그 벡터의 크기 제곱이 나옵니다. 하지만 원소끼리 곱하는 내적을 그대로 복소수에서 하면 크기가 복소수로 나오게 됩니다. 이 문제를 해소하기 위해서는 자연스럽게 내적할 때 하나의 수를 복소켤레를 취해서 곱하는 것을 생각할 수 있습니다. 이러한 내적을 이를 처음 고안한 샤를 에르미트의 이름을 따서 에르미트 내적이라고 합니다. 이때, 에르미트 내적은 실수끼리 하는 우리가 익숙한 내적을 포함하니 그냥 앞으로 하는 내적은 다 에르미트 내적이라고 생각합시다.

에르미트 내적 예시) \(\mathbb{C}^2\)의 벡터를 잡읍시다.

$$v=(1+2i,3+4i),u=(2-2i,7+5i)$$

$$\langle v,u \rangle=(1+2i)(3-4i)+(3+4i)(7-5i)=52+15i$$

$$\langle v,v \rangle=(1+2i)(1-2i)+(3+4i)(3-4i)=30$$

여기쯤 오면 왜 푸리에 급수 얘기는 안 하고 뜬금없이 벡터 얘기를 하고 있나 싶을 수 있습니다. 그 이유는 벡터공간에 대한 고찰이 푸리에 해석의 기초이자, 제 생각에 푸리에 급수를 이해하기 가장 좋은 방법이기 때문입니다.

위의 놀라운 사실을 직접 확인해보시길 권장합니다.

결국 우리는 어떤 구간에서의 함수를 벡터로 생각할 수 있는 것입니다! 그러면 당연히 이 벡터공간의 근간을 이루는 기저벡터가 무엇일지가 궁금할 수 있습니다.

결론부터 말하자면 \(e_n(\theta)=e^{2\pi i n\theta/L}\)일 때 \(\{e_n\}_{n\in\mathbb{Z}}\)이 이 공간의 정규직교기저를 이룹니다. 그리고 이런 통찰을 통해서 우리는 푸리에 급수를 함수가 벡터인 벡터공간의 벡터(=함수)를 그 기저벡터들의 선형결합으로 나타낸 것임으로 받아들일 수 있게 됩니다. 그리고 당연히 벡터공간의 기저벡터들로 그 안에 있는 모든 벡터들을 만들 수 있으니 푸리에 급수로 \(\mathcal{R}\)안의 모든 함수들이 표현 될 수 있다는 것을 당연히 여기게 될 수 있습니다.

위에서 한 말을 식으로 서술하자면, [0,2π]을 구간으로 정했을 때

$$f(x)=\sum_{n=-\infty}^{\infty}a_n e^{i n x}=\cdots+a_{-1}e^{i(-1)x}+a_{0}e^{i(0)x}+a_{1}e^{i(1)x}+\cdots$$

$$\simeq$$

$$v=\cdots+a_{-1}(\cdots,0,1,0,0,0,\cdots)+a_{0}(\cdots,0,0,1,0,0,\cdots)+a_{1}(\cdots,0,0,0,1,0,\cdots)+\cdots$$

그러면 이제\(\{e_n\}_{n\in\mathbb{Z}}\)이 정규직교기저를 이룬다는 것을 확인해봅시다!(어차피 한 구간에서 성립한다는 걸 보이면 선택된 구간이 다를 때는 똑같이 하면 되니 [0,2π]이 함수들이 정의 된 구간일 때로 해서 보이겠습니다)

일단 정규와 직교는 자명합니다.

-정규 = 크기가 1이다

\begin{equation*}
\begin{split}
\| e_n \|=\langle e_n,e_n \rangle &=\frac{1}{2\pi}\int_0^{2\pi}e^{in\theta}\overline{e^{in\theta}}d\theta \\
&=\frac{1}{2\pi}\int_0^{2\pi}e^{in\theta}e^{-in\theta}d\theta \\
&=\frac{1}{2\pi}\int_0^{2\pi}1d\theta=1
\end{split}
\end{equation*}

-직교 = 서로서로 내적했을 때 0이 나옴 (\(n\ne m\))

\begin{equation*}
\begin{split}
\langle e_n,e_m \rangle &=\frac{1}{2\pi}\int_0^{2\pi}e^{in\theta}\overline{e^{im\theta}}d\theta \\
&=\frac{1}{2\pi}\int_0^{2\pi}e^{in\theta}e^{-im\theta}d\theta \\
&=\frac{1}{2\pi}\int_0^{2\pi}e^{i(n-m)\theta}d\theta \\
&=\frac{1}{2\pi}\left[ \frac{1}{i(n - m)} e^{i(n - m)\theta} \right]_0^{2\pi} \\
&=\frac{1}{2\pi}\left( \frac{1}{i(n-m)}e^{i(n-m)2\pi}-\frac{1}{i(n-m)}e^{i(n-m)0} \right) \\
&=\frac{1}{2\pi}\left( \frac{1}{i(n-m)}-\frac{1}{i(n-m)} \right)=0
\end{split}
\end{equation*}

-기저 = 이 집합의 벡터들의 선형결합으로 주어진 벡터공간의 임의의 벡터를 만들 수 있다.

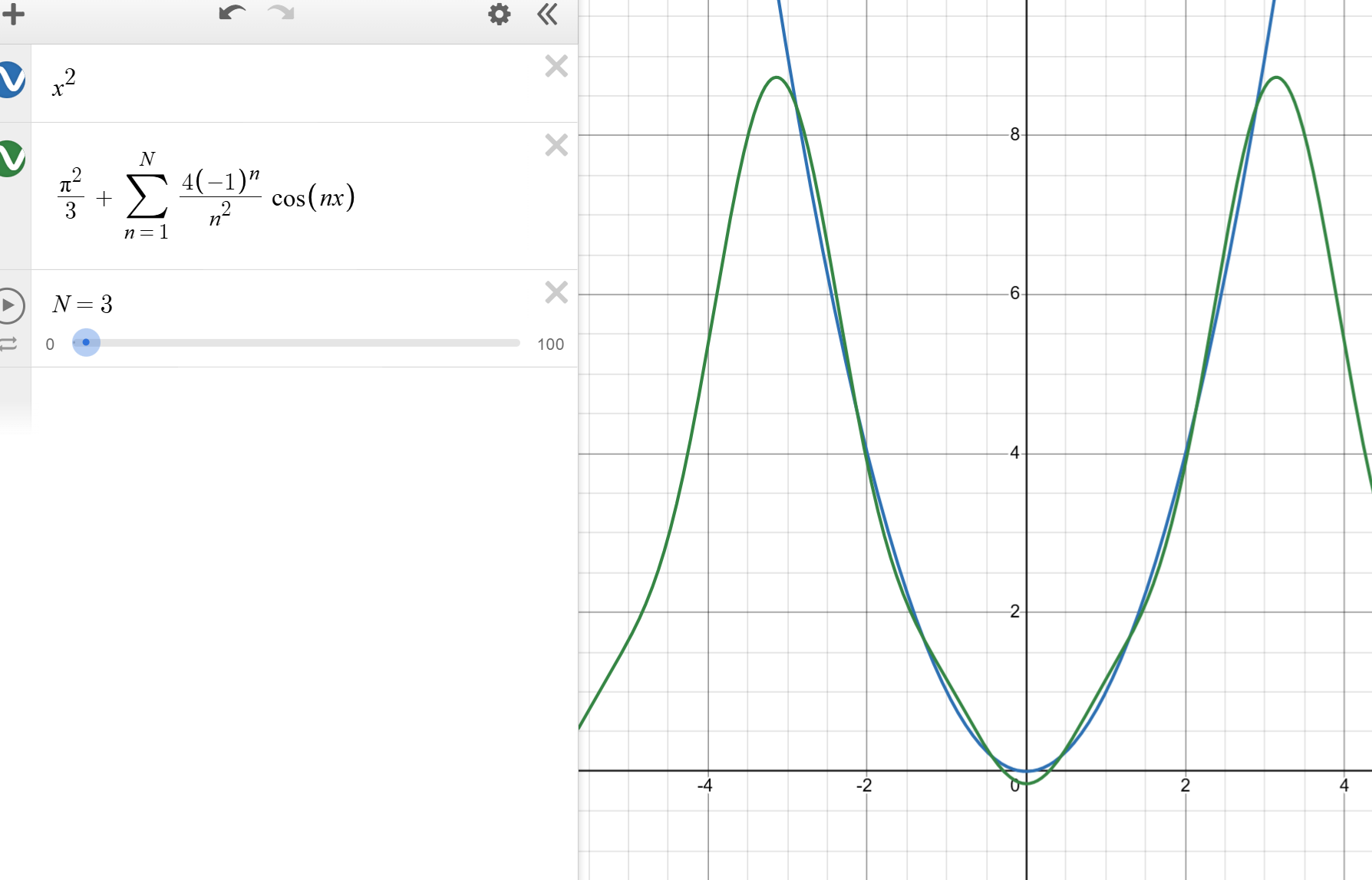
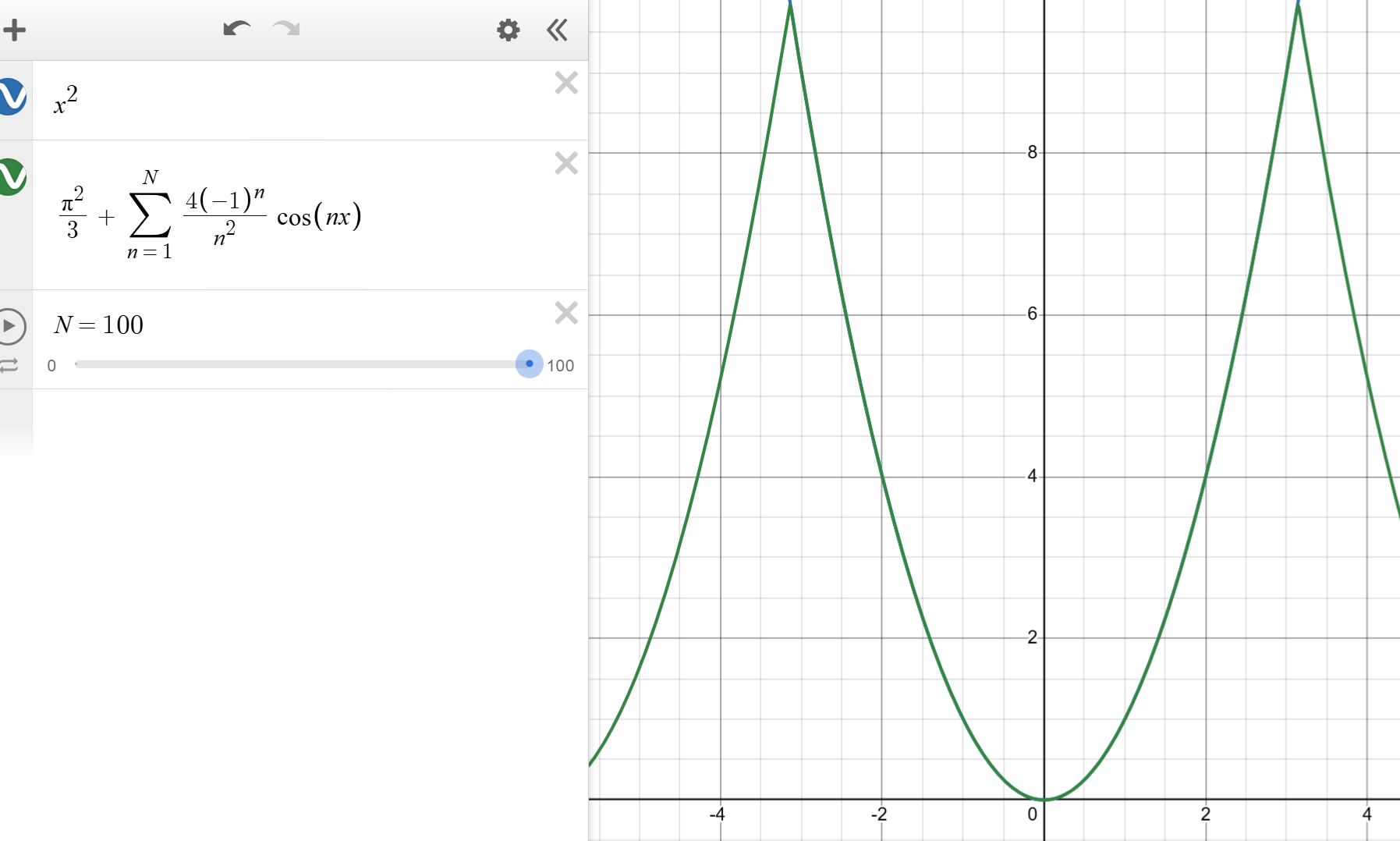
이걸 증명하려면 결국 푸리에 급수의 수렴성을 증명해야 됩니다. 으엑. 글이 너무 길어지고, 단순한 소개가 아니게 돼서 푸리에 급수의 제곱평균수렴성은 독립된 글에서 증명하겠습니다.

위 정리에 따라서 N이 무한대로 가면, 즉 \(\{e_n\}_{n\in\mathbb{Z}}\) 안의 모든 함수들을 더하면, \(\{e_n\}_{n\in\mathbb{Z}}\) 안 모든 함수들과 f를 뺀 벡터의 크기는 0이 되고, 따라서 선형결합으로 이루어진 꼴과 원 함수는 같게 됩니다.

마지막으로, 푸리에 급수의 계수에 대해 설명하려고 합니다. 푸리에 급수가 기저벡터들의 합으로 나타내어진 것이라면, 각 기저벡터 앞에 곱해지는 계수는 그 기저벡터의 방향으로 우리가 표현하고자 하는 벡터의 그 기저벡터방향 성분이어야 할 것입니다. 벡터에 대한 걸 대충 배우셨으면, 어떤 벡터가 다른 벡터의 방향으로 얼마만큼 성분이 있는지 알고 싶을 땐 내적을 한다는 걸 아실 겁니다. 따라서 푸리에 계수는 그 계수가 붙어있는 기저벡터와 우리 표현하고자 하는 함수의 내적으로 정의됩니다.

위 설명의 이해를 돕기 위함 예시)

$$(5,-7,6)=a_1(1,0,0)+a_2(0,1,0)+a_3(0,0,1)$$

$$a_1=\langle(5,-7,6),(1,0,0)\rangle=5$$

$$a_2=\langle(5,-7,6),(0,1,0)\rangle=-7$$

$$a_3=\langle(5,-7,6),(0,0,1)\rangle=6$$

$$\therefore (5,-7,6)=5(1,0,0)+-7(0,1,0)+6(0,0,1)$$

그래서 푸리에 계수와 그를 앞에 붙인 푸리에 급수는 다음과 같이 표현되는 것입니다.

$$a_n=\langle f(x),e^{2\pi inx/L}\rangle=\frac{1}{L}\int_{a}^{b}f(x)e^{-2\pi i n x/L}dx \, \, \, \, (L=b-a)$$

$$\therefore f(x)=\sum_{n=-\infty}^{\infty}a_ne^{2\pi i n x/L}$$

진짜 마지막으로 하나만 더하자면, 위 함수 f는 벡터공간의 원소로 봤을 땐 구간 [a,b]에서만 정의되지만, 복소지수함수는 주기함수여서 저 푸리에 급수는 주기 L로 반복 돼서 실수축에서 정의가 됩니다.

결국 이 글을, 읽으시면서 푸리에 급수가 한 벡터를 기저벡터들의 합으로 나타낸 것이라는 것을 이해하셨으면 제가 가장 전달하고자 한 것을 받으신 겁니다. 읽어주셔서 감사합니다!

여기서 푸리에 급수가 복소지수함수로 나타내어졌다가, 사인 코사인으로 나타내어져서 이게 뭔가 하실 수도 있을 것 같습니다. 사실 정규직교기저가 \(\{e_n\}_{n\in\mathbb{Z}}\)만 있는 게 아니라 \(\{sin(n\theta),cos(n\theta)\}_{n\in\mathbb{Z}^+}\)도 됩니다. 이들은

$$ f(x)=\sum_{n=-\infty}^{\infty}c_ne^{ i n x}=a_0+\sum_{n=1}^\infty a_n cos(nx)+\sum_{n=1}^\infty a_n sin(nx)$$ 이어서 각 n마다 비교하면

$$c_n e^{inx}+c_{-n} e^{-inx}=a_ncos(nx)+b_nsin(nx)$$

$$cos(nx)=\frac{e^{inx}+e^{-inx}}{2}이고 \, \, sin(nx)=\frac{e^{inx}-e^{-inx}}{2i}입니다$$ 따라서 각 항마다 비교하면

$$c_n=\frac{a_n+ib_n}{2}, \, c_{-n}=\frac{a_n-ib_n}{2}$$ 으로서 결국 서로 같습니다.

\(\mathbb{R}^2\)평면에서도 정규직교기저가 (1,0),(0,1)만 있는 게 아니라 \((\frac{\sqrt2}{2},\frac{\sqrt2}{2}),(-\frac{\sqrt2}{2},\frac{\sqrt2}{2}) \) 도 있는 것 같은 것 아니면 그냥 복소지수함수를 오일러 공식으로 풀어쓴 것으로 생각해도 좋을 것 같습니다.