FA-3 푸리에 급수의 유일성

오늘은 Elias M. Stein과 Rami Sakarchi의 [STEIN 푸리에 해석학]에서 소개된 푸리에 급수의 유일성의 증명을 알아봅니다. 사실 그냥 책을 직접 읽어도 되지만, 이 글에선 최대한 자세하게 증명을 설명하려고 합니다. 푸리에 급수가 뭔지에 대해 대충 아셔야 하니 앞선 푸리에 해석 글들을 읽어보시는 걸 추천합니다.

전 글에서도 했듯이, 어차피 구간을 어떻게 잡던 쓰는 논리는 달라지지 않으니 푸리에 급수의 구간을 표기가 편한 구간 [-π,π]로 잡읍시다. 우리가 증명하고 싶은 정리는 다음과 같습니다

\(h(\theta)=f(\theta)-g(\theta)\)인 \(h(\theta)\)를 두면

위 명제는 다음과 같다는 걸 확인 할 수 있습니다.

h가 적분가능한 함수이고, h의 모든 푸리에 계수가 0이면, 연속인 점 \(\theta_0\)에서 \(h(\theta_0)=0\)이다.

이 명제를 보고

$$f(\theta_0)=\sum_{n=-\infty}^{\infty}0 e^{in\theta_0}=0$$

이니까 "어 이거 자명한 거 아닌가?"라고 당연히 생각이 들 수 있습니다. 우리가 이것을 증명해야 되는 이유는 푸리에 계수가 적분으로 정의되기 때문입니다.

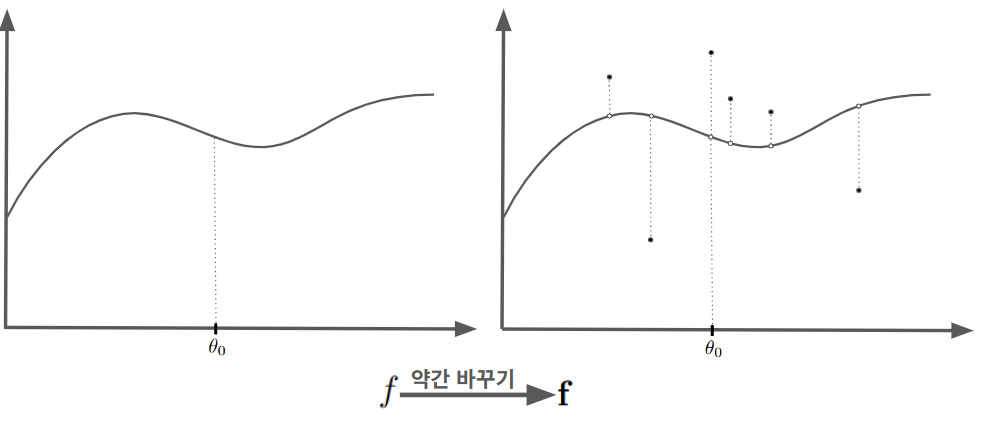
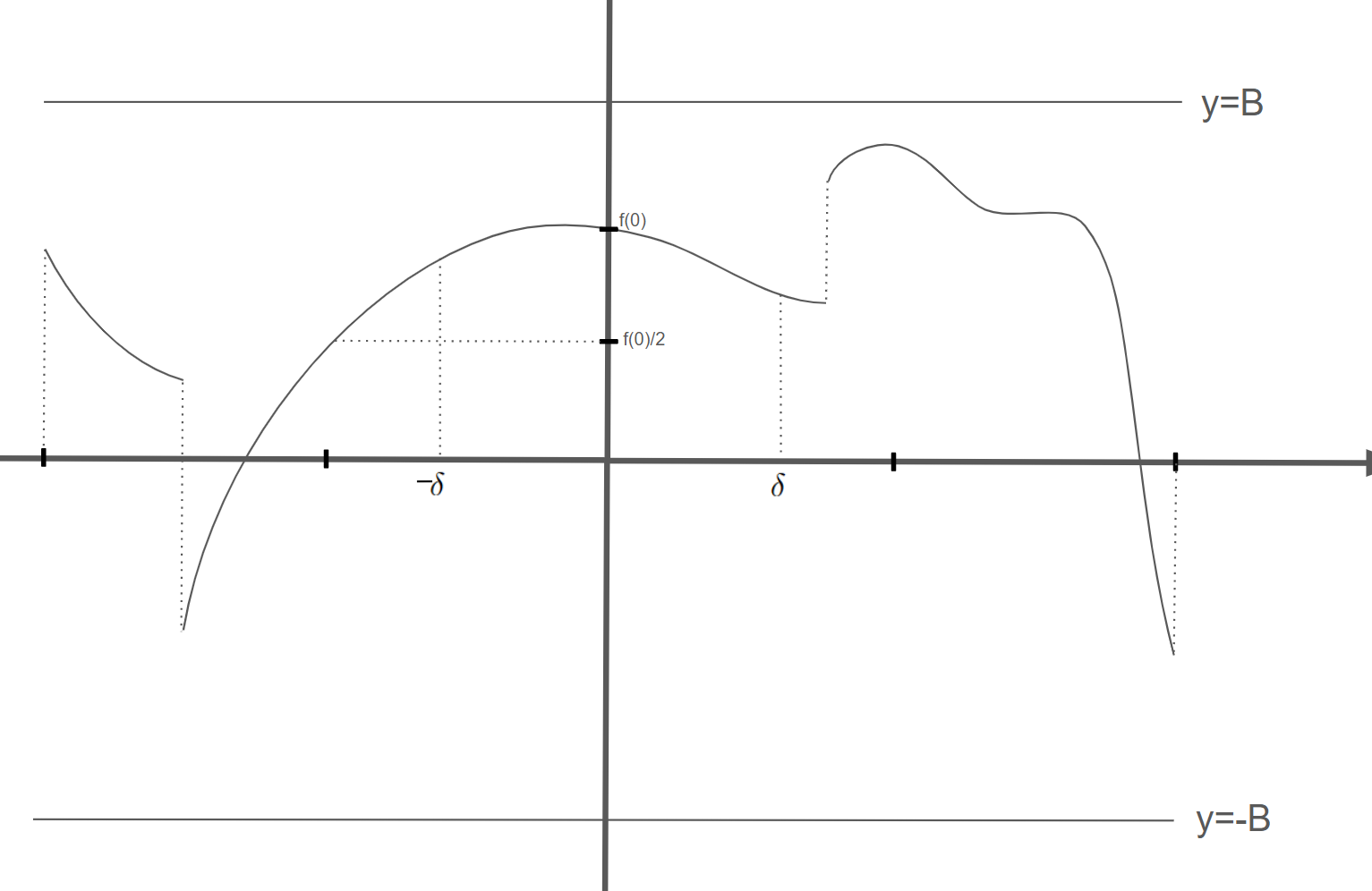
위 그림을 보면

$$\int f(\theta)d\theta=\int\mathbf{f}(\theta)d\theta$$

$$f(\theta_0)\neq \mathbf{f}(\theta_0)$$

임을 확인할 수 있는데, 따라서 이를 통해서 푸리에 급수로 나타냈을 때 계수가 같아도 두 함수가 특정 점들에선 값이 다를 수 있다는 것을 확인 할 수 있습니다(정확히는 측도가 0인 점들의 집합에서(=무시할 만큼 적은 양의 점들)).

우리는 여기에 연속 조건을 더했을 때 유일성이 성립하는지 보고 싶은 겁니다.

증명의 계획은 굉장히 간단합니다. 귀류법을 써서, \(f(\theta_0)\neq 0\)이라고 합니다. 일반성을 잃지 않고, f가 [-π,π]에서 정의되어 있고, \(\theta_0=0\), 그리고 f(0)>0이라고 둡니다.

(왜냐하면 예를 들어서 \(\theta_0=\pi/6\)였으면 f를 주기함수로 하고 \(\pi/6\)이 0에 오게 평행이동 시키고 나서 [-π,π]에서 정의되게 하면 같은 논법 적용 가능, 그리고 f(0)<0이어도 똑같은 논법 적용 가능)

그렇게 둔 후 0에서 엄청 커지는 삼각다항식들을{\(p_k(\theta)\)} 만드는 겁니다. f의 모든 푸리에 계수가 0이니 \(\int_0^{2\pi}f(\theta)p_k(\theta)d\theta\)=0이어야 되는데, \(k \to \infty\)가 됨에 따라 저 적분이 발산함을 보여서 모순을 찾는 것입니다.

(삼각다항식은 \(P(x)=\sum_{n=-N}^{N}a_n e^{inx}\)으로 나타내지는 모든 함수입니다(여기 참고) 그래서 f의 모든 푸리에 계수가 0임을 이용해서

\begin{equation*}
\begin{split}
\int_{-\pi}^{\pi}f(\theta)p_k(\theta)d\theta&=\int_{-\pi}^{\pi}f(\theta)\sum_{n=-N}^{N}a_n e^{in\theta}d\theta \\
&=\sum_{n=-N}^{N}a_n\int_{-\pi}^{\pi}f(\theta) e^{in\theta}d\theta =0
\end{split}
\end{equation*}

인 것입니다.)

삼각다항식은 다음과 같이 정합니다:

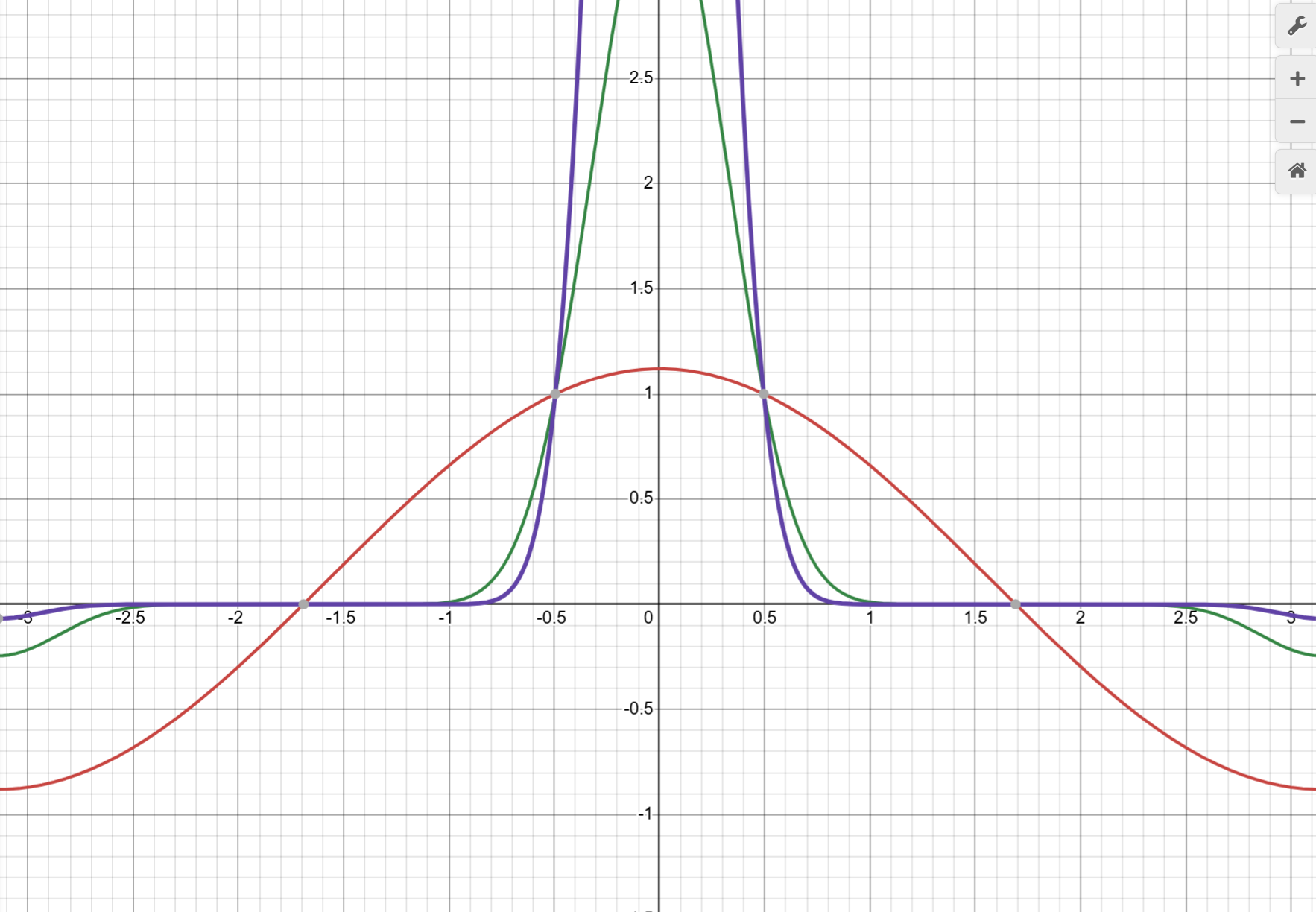
$$p(\theta)=\epsilon+\cos(\theta) \, , \, \, p_k(\theta)=(\epsilon+\cos(\theta))^k$$

조건에 의해서 0에서 함수 f는 연속이니, 엡실론 델타 논법으로 정의한 연속을 생각해서

$$\forall \epsilon' > 0 \, \, \, \exists \delta >0 \, \, \, s.t. $$

$$|\theta-0|<\delta \Rightarrow |f(\theta)-f(0)|<\epsilon'$$

이니, \(\epsilon'=f(0)/2\)로 두면 \(|\theta|<\delta\)일 때 \(f(\theta)>f(0)/2\)이고 \(0<\delta<\pi/2\)인 \(\delta\)를 잡을 수 있습니다.

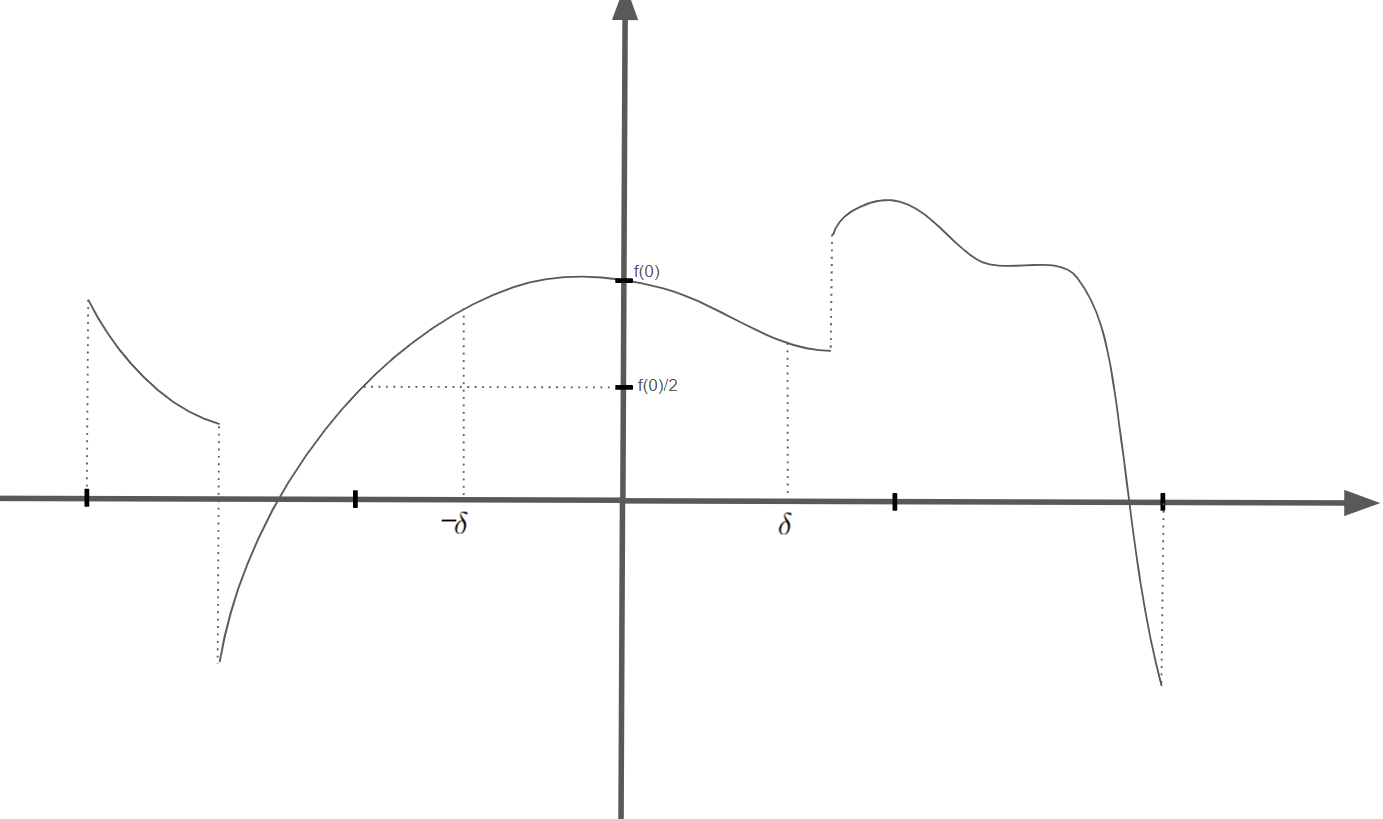
그리고 \(\epsilon\)을 \(\delta<|\theta|\leq\pi\)일 때 \(|p(\theta)|<1-\epsilon/2\)이 되게 충분히 작게 잡습니다.

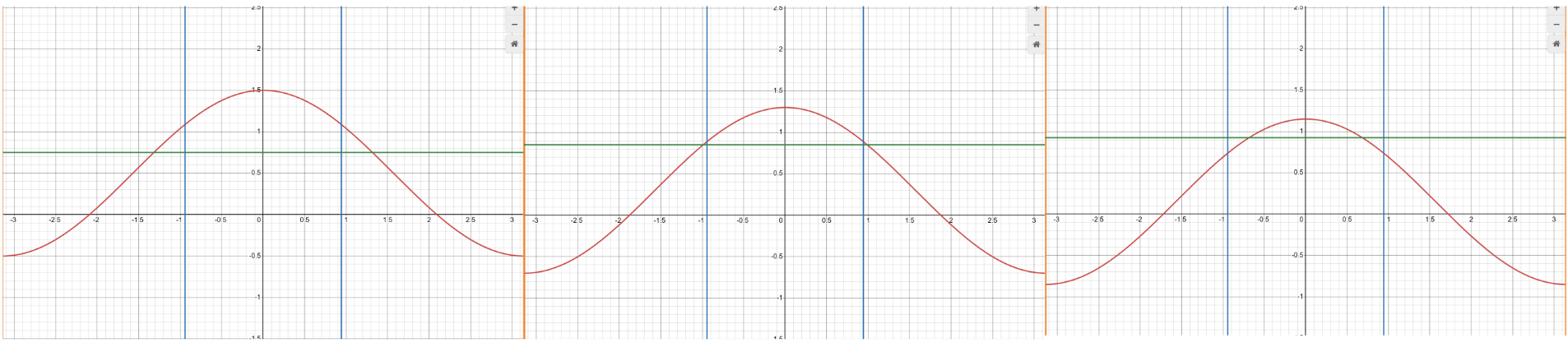
또, \(|\theta|<\eta\)이면 \(p(\theta)>1+\epsilon/2\)이게 \(0<\eta<\delta\)인 \( \eta \)를 잡읍시다.

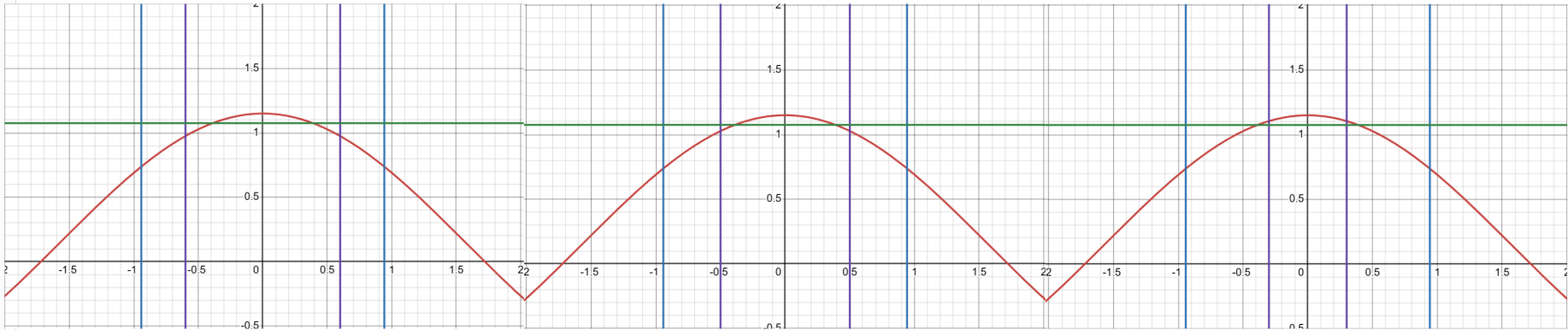
마지막으로 f는 적분 가능한 함수이니 모든 \(\theta\)에 대해 \(|f(\theta)|\leq B\)인 바운드 B를 잡으면

$$\int_{-\pi}^{\pi}f(\theta)p_k(\theta)d\theta$$

위 적분을 \(|\theta|\)의 \([0,\eta], ( \eta ,\delta],(\delta,\pi]\)의 세 개의 구간으로 나눠서 분석할 수 있습니다.

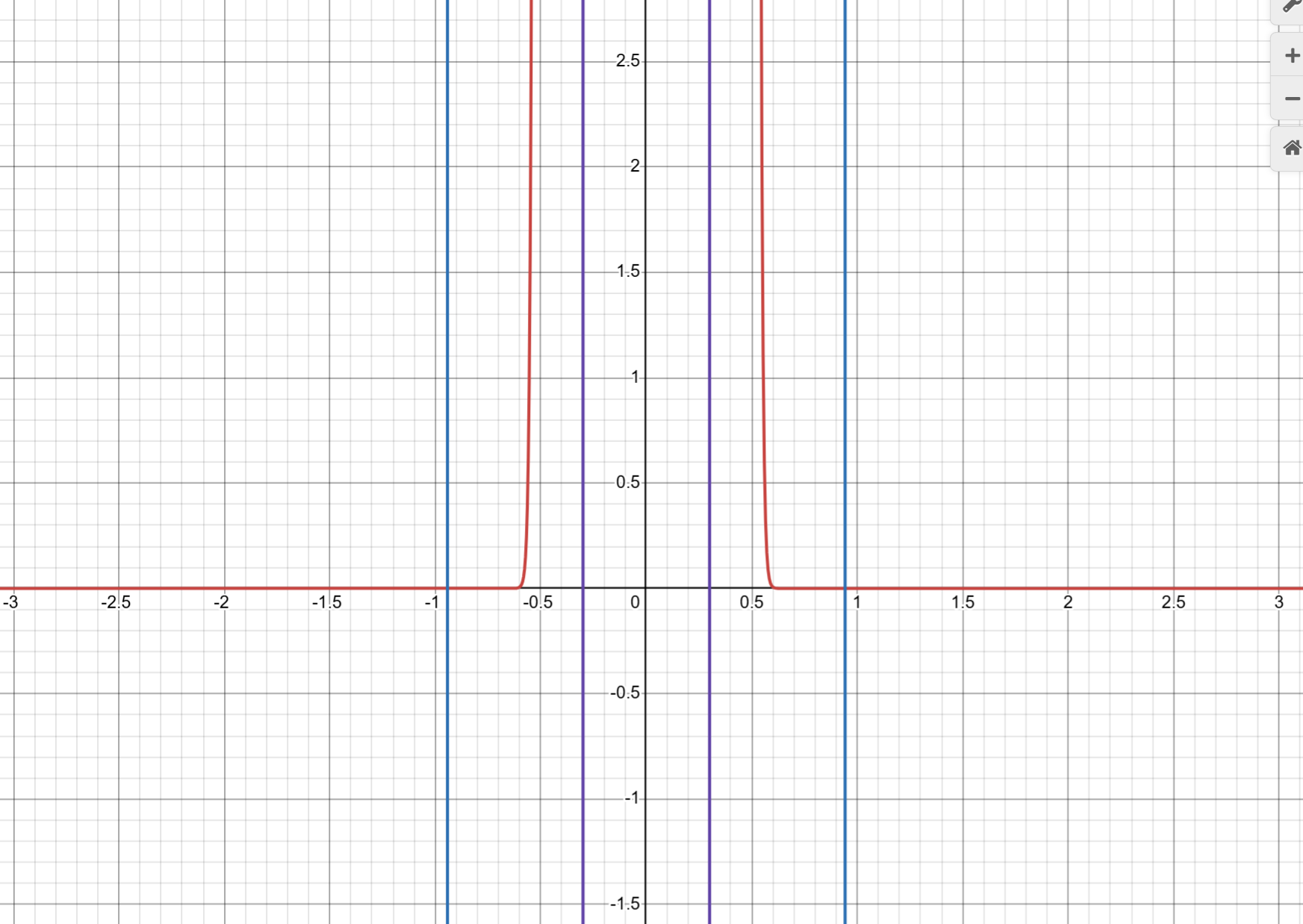
1-\((\delta,\pi]\)

-(적분 구간 크기)=\(2(\pi-\delta)\)

-\(f(\theta)\leq B\)

-\(p_k(\theta)<(1-\epsilon/2)^k\)

$$\therefore|I_1|= \left| \int_{|\theta|>\delta}f(\theta)p_k(\theta)d\theta \right|\leq 2(\pi-\delta)B(1-\epsilon/2)^k$$

이어서 \((1-\epsilon/2)^k\)항에 의해서 k가 무한대로 감에 따라서 적분값은 0으로 갑니다.

2-\(( \eta ,\delta]\)

-(적분 구간 크기)=\(2(\delta-\eta)>0\)

-\(f(\theta)>f(0)/2\)

-\(p_k(\theta)>\epsilon^k \, \, (\because |\theta|<\delta<\pi/2 \Rightarrow p(\theta)=\epsilon+\cos(\theta)>\epsilon)\)

$$\therefore I_2=\int_{\eta<|\theta|\leq\delta}f(\theta)p_k(\theta)d\theta>0$$

3-\([0,\eta]\)

-(적분 구간 크기)=\(2\eta\)

-\(f(\theta)>f(0)/2\)

-\(p_k(\theta)>(1+\epsilon/2)^k\)

$$\therefore I_3=\int_{|\theta|\leq\eta}f(\theta)p_k(\theta)d\theta>\eta f(0)(1+\epsilon/2)^k $$

따라서 이 적분값은 \((1+\epsilon/2)^k\)에 의해서 k가 무한대로 감에 따라서 양의 무한대로 발산합니다.

그래서 by 1,2,3

$$\int_{-\pi}^{\pi}f(\theta)p_k(\theta)d\theta=I_1+I_2+I_3>I_3$$

$$\therefore \int_{-\pi}^{\pi}f(\theta)p_k(\theta)d\theta\to \infty \, \, \, as \, \, \, k\to \infty$$

따라서 모순이 발생해서 유일성 정리는 참이 됩니다.