Free Rotation of a Rigid Body

Physics Aug 11, 2025

과학적으로 중요하게 사용된 개념에는 하이라이트를 하였다.

Introduction

이 글을 읽기 전에 자신의 핸드폰을 특정 축을 기준으로 회전 시키며 위로 던져보자. ~~핸드폰은 모두 무사한가요?~~

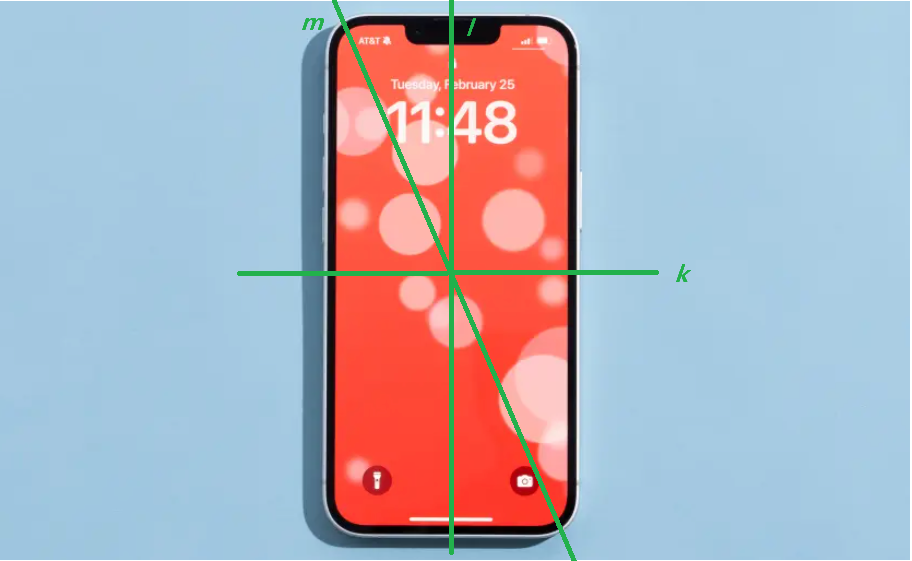
k, l, m 축을 기준으로 회전시키며 던져보면 각 회전마다 특징이 있다는 것을 알 수 있다. 필자의 기억이 틀리지 않았다면 ~~(한번 믿어보자)~~ k, l 축을 기준으로 회전시켰을 경우 회전축의 방향이 그대로 유지되지만, m 축을 기준으로 회전시키면 공중에서 회전축의 방향이 이리저리 바뀌는 것을 관찰할 수 있다. 왜 이러한 현상이 발생하는 것일까? 수식적으로 알아보도록 하자.

Analysis

분석에 앞서서...

가장 먼저 회전을 설명할 때 빠질 수 없는 개념인 회전 관성에 대해서 알 필요가 있다. 아래의 설명을 이해하기 위해서는 기본적으로 알고 있는 회전 관성에 대한 개념보다 조금 더 깊이 있게 이해할 필요가 있기 때문에 위키피디아에서 읽어보고 오도록 하자. ~~위키피디아를 믿자!~~

참고 : 아래 글에서는 관성 텐서를 표현할 때 \(\overset{\leftrightarrow}{\textbf{I}}\) 을 사용했다.

본격적인 분석

먼저 Frame 을 잘 설정할 필요가 있다. 분석을 용이하게 하기 위해서 \(O-xyz\)라는 Frame 을 잡을 것이다. 이때, \(x, y, z\) 축은 강체의 주축 (관성의 곱이 모두 0 이 되도록 하는 축) 이 되도록 한다. 주축은 위의 조건을 만족해야 하므로 자연스럽게 강체에 붙어서 같이 회전하게 된다. 그림에 표현하면 아래와 같다. 참고로 \(\vec{\omega}\) 는 각속도 벡터이다.

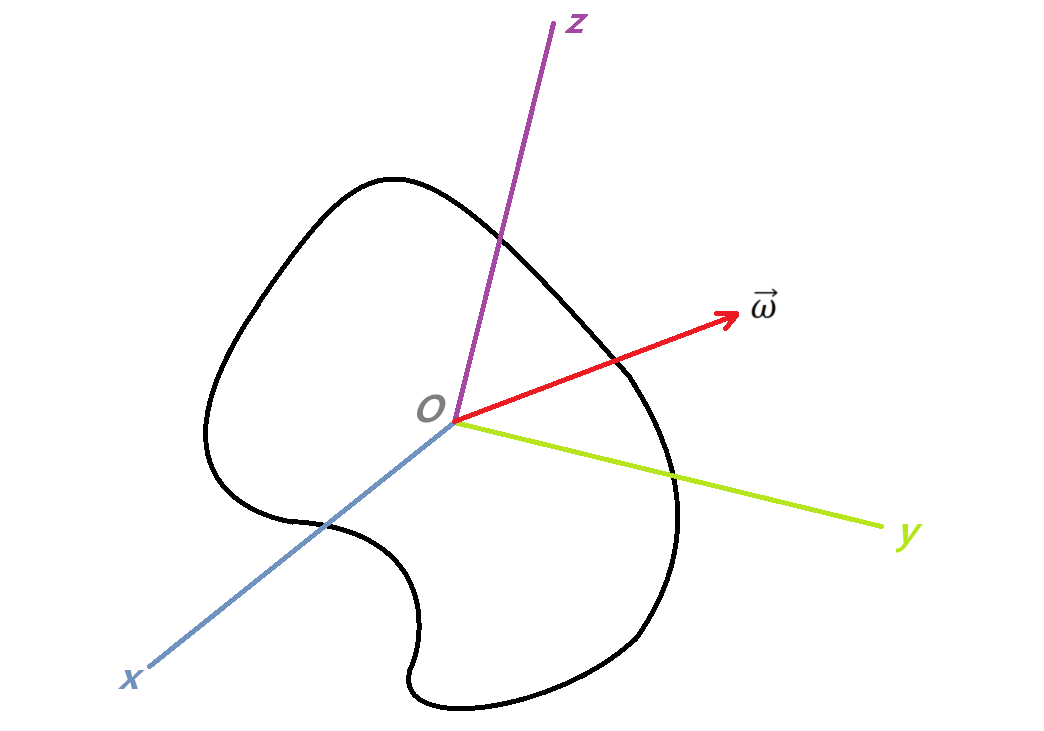
참고 : 일반적으로 3개의 서로 수직한 주축을 잡을 수 있다는 것은 증명이 가능하다. 다만 증명의 과정이 상당히 복잡하고 수학적인 관계로 (필자도 잘 모른다) 증명은 생략하겠다.

이 Frame 에서 강체가 회전을 할 때, \(\vec{L}\) (=각 운동량 벡터) 과 \(T\) (=운동에너지) 가 보존된다는 사실을 알 수 있다. 이제 위 보존량들을 회전 관성과 각속도의 식으로 표현해보자.

각 운동량 (\(\vec{L}\))

\(O-xyz\) 가 주축 Frame 이므로 관성의 곱이 모두 0이다. 따라서 이 Frame 에 대한 관성 텐서는,

\[\overset{\leftrightarrow}{\textbf{I}} = \begin{bmatrix}
I_x & 0 & 0 \\
0 & I_y & 0 \\
0 & 0 & I_z
\end{bmatrix}\]

로 표현된다. 이때 \(\vec{L} = \overset{\leftrightarrow}{\textbf{I}}\cdot\vec{\omega}\) 이므로,

\[\vec{L} = \overset{\leftrightarrow}{\textbf{I}}\cdot\vec{\omega}\
\begin{bmatrix}
I_x & 0 & 0 \\
0 & I_y & 0 \\
0 & 0 & I_z
\end{bmatrix}\begin{bmatrix}
\omega_x \\
\omega_y \\
\omega_z
\end{bmatrix}=\begin{bmatrix}
I_x \omega_x \\
I_y \omega_y \\
I_z \omega_z
\end{bmatrix}
\]

여기에서 \(\vec{L}\cdot\vec{L}\) 이 보존되기 때문에,

\[I_x^2 \omega_x^2 + I_y^2 \omega_y^2 + I_z^2 \omega_z^2 = \text{const.}\]

운동에너지 (\(T\))

회전하는 강체에서의 운동에너지는 \(T = \frac{1}{2} \vec{\omega}\cdot\overset{\leftrightarrow}{\textbf{I}}\cdot\vec{\omega}\) 로 나타나므로,

\[
T = \frac{1}{2}\begin{bmatrix}
\omega_x & \omega_y & \omega_z
\end{bmatrix}\begin{bmatrix}
I_x & 0 & 0 \\
0 & I_y & 0 \\
0 & 0 & I_z
\end{bmatrix}\begin{bmatrix}
\omega_x \\
\omega_y \\
\omega_z
\end{bmatrix}
= \frac{1}{2} \left( I_x \omega_x^2 + I_y \omega_y^2 + I_z \omega_z^2 \right)
\]

그리고 \(T\) 가 보존량이므로,

\[ I_x \omega_x^2 + I_y \omega_y^2 + I_z \omega_z^2 = \text{const.}\]

대략적인 연립의 개요

위의 두 보존량 조건을 모두 만족해야 하므로, 다음의 연립 방정식을 풀면 된다.

\[
\begin{cases}
I_x^2 \omega_x^2 + I_y^2 \omega_y^2 + I_z^2 \omega_z^2 = \text{const.}\\
I_x \omega_x^2 + I_y \omega_y^2 + I_z \omega_z^2 = \text{const.}
\end{cases}
\]

타원체 연립의 예시 ~~TMI : 필자가 그린 것은 아니다. 고마워요 그림작가!~~

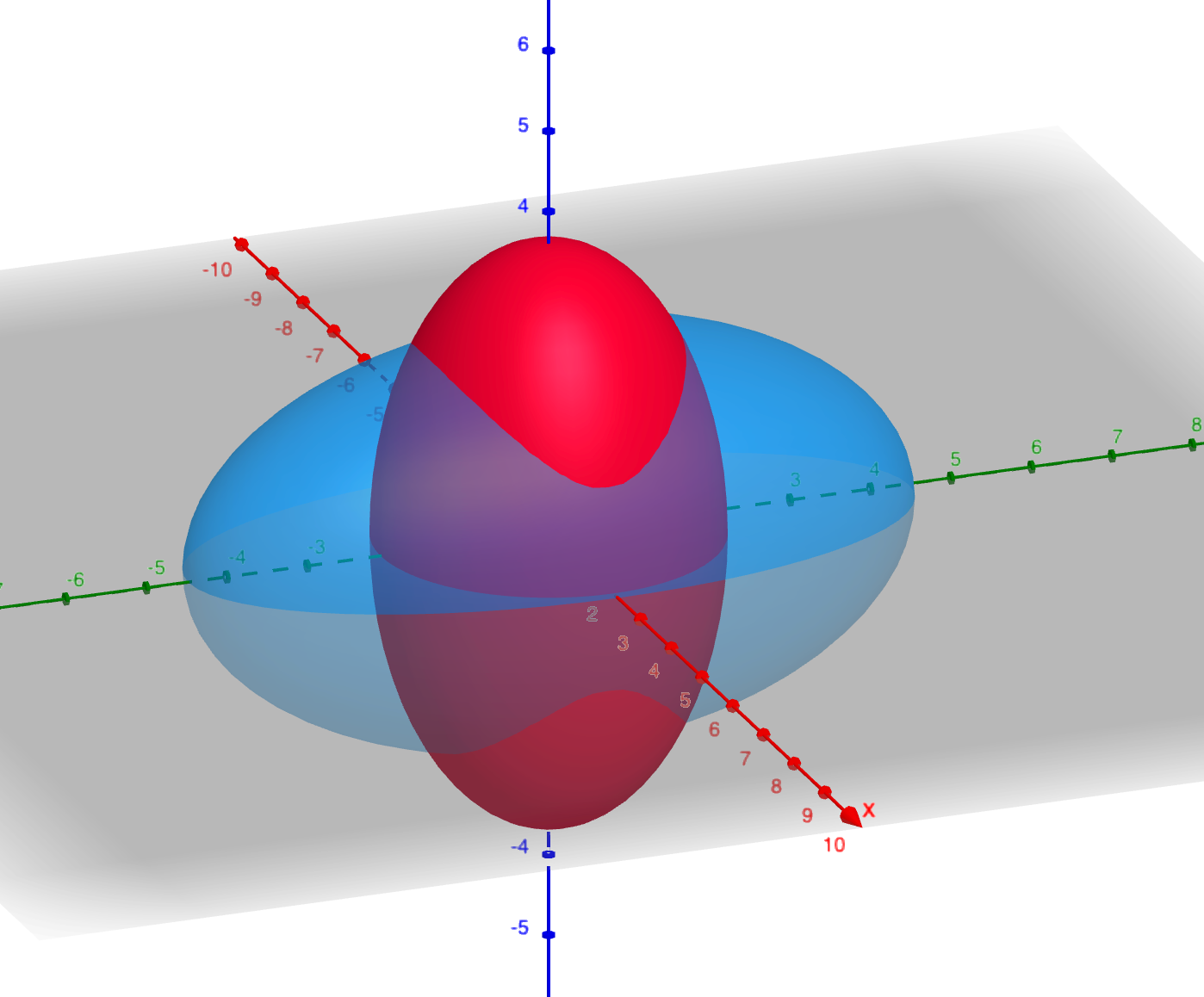
위의 두 식은 각각 타원체를 나타낸다. 따라서 위의 예시 그림처럼, 두 타원체의 교선 위에서 \(\vec{\omega}\) 가 이동할 것임을 알 수 있다. 따라서 우리는 초기 조건에 따라 타원체가 어떠한 형태를 가지는지 분석하여 초기 조건에 따른 물체의 회전 운동을 분석할 것이다.

구체적인 연립

상황마다 다르게 생긴 타원체를 모두 그리는 것은 필자 ~~or 그림작가~~에게는 너무나 가혹한 행위라고 생각되기 때문에 말로 때우도록 하겠다.
\(I_x < I_y < I_z\) 로 가정한다.

Case 1) \(\overset{\longrightarrow}{\omega_0} = (\omega_0,0,0)\) 인 경우

1. 각 운동량 (\(\vec{L}\)) 보존
\[I_x^2 \omega_0^2 = I_x^2 \omega_x^2 + I_y^2 \omega_y^2 + I_z^2 \omega_z^2 \\
\quad\Rightarrow\quad |\omega_x| \leq \omega_0, \quad |\omega_y| \leq \frac{I_x}{I_y} \omega_0, \quad |\omega_z| \leq \frac{I_x}{I_z} \omega_0\]

2. 운동에너지 (\(T\)) 보존
\[I_x \omega_0^2 = I_x \omega_x^2 + I_y \omega_y^2 + I_z \omega_z^2 \\
\quad\Rightarrow\quad |\omega_x| \leq \omega_0, \quad |\omega_y| \leq \sqrt{\frac{I_x}{I_y}} \omega_0, \quad |\omega_z| \leq \sqrt{\frac{I_x}{I_z}} \omega_0\]

위에서 도출된 범위 조건들로 각 타원체의 \(x, y, z\) 절편을 결정하면, 전체적으로는 \((\vec{L} 보존 타원체) \subseteq (T 보존 타원체)\) 의 형태가 나오고, \(x = \pm \omega_0\) 에서만 두 타원체의 교점이 생기게 된다. 따라서 \(\vec{\omega} = \overset{\longrightarrow}{\omega_0}\) 이고 이 식은 회전축이 처음의 회전축과 일치함을 나타낸다.

Case 2) \(\overset{\longrightarrow}{\omega_0} = (0,0,\omega_0)\) 인 경우

1. 각 운동량 (\(\vec{L}\)) 보존
\[I_z^2 \omega_0^2 = I_x^2 \omega_x^2 + I_y^2 \omega_y^2 + I_z^2 \omega_z^2 \\
\quad\Rightarrow\quad |\omega_x| \leq \frac{I_z}{I_x} \omega_0, \quad |\omega_y| \leq \frac{I_z}{I_y} \omega_0, \quad |\omega_z| \leq \omega_0\]

2. 운동에너지 (\(T\)) 보존
\[I_z \omega_0^2 = I_x \omega_x^2 + I_y \omega_y^2 + I_z \omega_z^2 \\
\quad\Rightarrow\quad |\omega_x| \leq \sqrt{\frac{I_z}{I_x}}, \omega_0 \quad |\omega_y| \leq \sqrt{\frac{I_z}{I_y}} \omega_0, \quad |\omega_z| \leq \omega_0\]

마찬가지의 방법으로 진행하면, 이번에는 \((T 보존 타원체) \subseteq (\vec{L} 보존 타원체)\) 의 형태가 나오고, \(z = \pm \omega_0\) 에서만 두 타원체의 교점이 생기게 된다. 따라서 이번에도 \(\vec{\omega} = \overset{\longrightarrow}{\omega_0}\) 이고 초기의 회전축과 나중의 회전축이 일치한다는 것을 알 수 있다.

Case 3) \(\overset{\longrightarrow}{\omega_0} = (0,\omega_0,0)\) 인 경우 (이 경우는 조금 다르다!)

1. 각 운동량 (\(\vec{L}\)) 보존
\[I_y^2 \omega_0^2 = I_x^2 \omega_x^2 + I_y^2 \omega_y^2 + I_z^2 \omega_z^2 \\
\quad\Rightarrow\quad |\omega_x| \leq \frac{I_y}{I_x} \omega_0, \quad |\omega_y| \leq \omega_0, \quad |\omega_z| \leq \frac{I_y}{I_z} \omega_0\]

2. 운동에너지 (\(T\)) 보존
\[I_y \omega_0^2 = I_x \omega_x^2 + I_y \omega_y^2 + I_z \omega_z^2 \\
\quad\Rightarrow\quad |\omega_x| \leq \sqrt{\frac{I_y}{I_x}} \omega_0, \quad |\omega_y| \leq \omega_0, \quad |\omega_z| \leq \sqrt{\frac{I_y}{I_z}} \omega_0\]

드디어 마지막으로 위에서 도출된 범위 조건들로 각 타원체의 \(x, y, z\) 절편을 결정하면, \(x\) 절편은 \(\vec{L}보존 타원체\) 가 더 크고, \(y\) 절편은 두 타원체가 같고, \(z\) 절편은 \(T 보존 타원체\) 가 더 크다. 따라서 필연적으로 두 타원체의 교선이 생기게 되고, 그 교선을 따라서 각속도 벡터가 이동한다는 것을 알 수 있다. 즉, 회전축이 계속 바뀌게 된다!

처음의 예시의 경우에 대입해본다면, k 축과 l 축은 Case 1 과 Case 2 와 비슷한 상황으로 볼 수 있고, m 축은 Case 3 와 비슷한 상황으로 볼 수 있다. ~~짜라란~~

Conclusion

나름 제목에 강체의 자유 회전이라고 써 놓았지만, 글에서 설명하는 과정에 있어서 초기 조건이 굉장히 단순했다는 것을 감안하면, 완벽하게 일반화를 한 상황은 아니다. (실제로 일반적인 초기 조건의 해는 타원적분을 포함하는 형태가 나온다고 한다 ~~심심한 사람은 한번 유도해보자~~) 따라서 이런 느낌으로 생각을 하고 설명을 하는구나 정도로만 생각하자. 필자의 지식이 매 글에서 강조했다시피 굉장히 얕기 때문에 잘 가려서 읽으면 될 것 같다. 이상한 것이 있으면 직접 찾아보고 이해하도록 하자. 또한 오류 수정이 많을수록 더 나은 글이 될 수 있으므로 틀린 내용이 있다면 꼭 댓글로 제보해주기를 바란다.