General Relativity

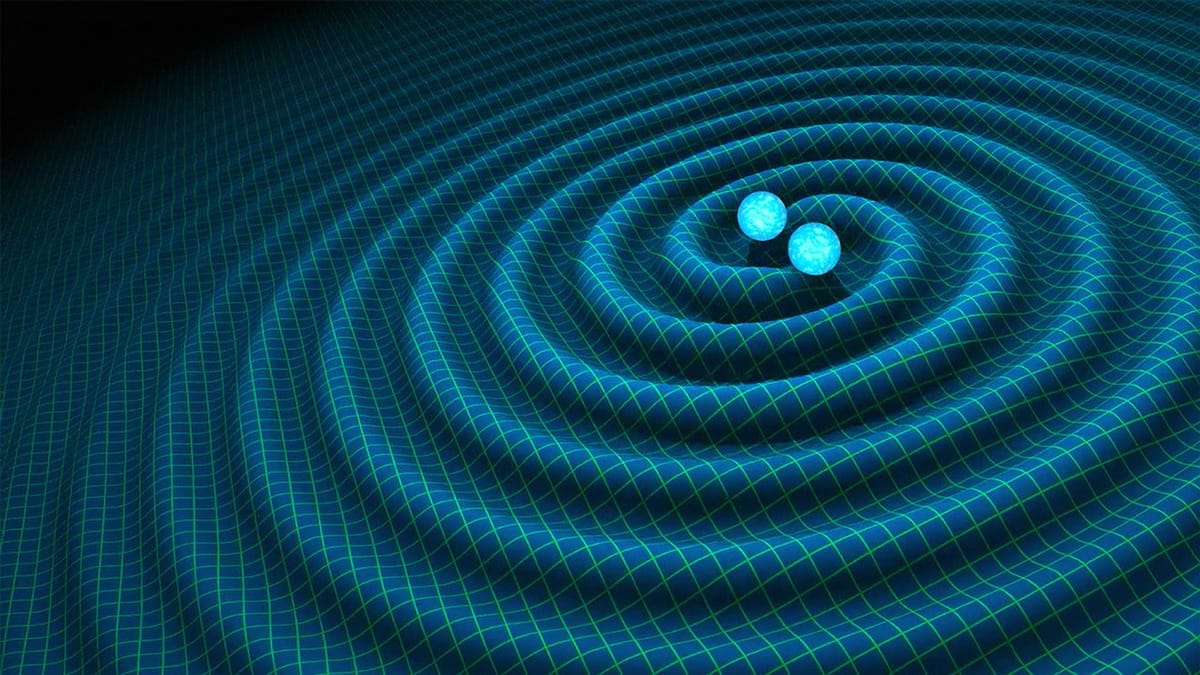
Albert Einstein's General Theory of Relativity(GR), unveiled in 1915, completely revolutionized our understanding of gravity, moving far beyond Issac Newton's concept of a mysterious "action at a distance" force. Newton describes gravity as a force pulling objects together. Einstein, however, proposed something far more elegant and profound : gravity is not a force, but a manifestation of the curvature of spacetime itself, caused by the presence of mass and energy.

Following is simple modeling and imagination of this. Imagine a heavy bowling ball placed on a stretched rubber sheet, causing it to sag. If you then roll smaller marbles across the sheet, they won't simply roll in straight lines; they'll curve inwards towards the bowling ball. The marbles aren't being 'pulled' by the bowling ball in the Newtonian sense; they are simply following the "straightest possible paths" on the now-curved surface. The crucial difference here is that the 'sheet' isn't just a separate background; it is space and time.

The Grand Choreography of Spacetime

The core insight of GR is deceptively simple yet incredibly powerful : Mass and energy tell spacetime how to curve, and curved spacetime tells mass and energy how to move.

• Spacetime is a Dynamic Fabric : Our familiar 3-dimensional space and 1-dimensional time are not independent entities but are interwoven into a unified, dynamic 4-diensional continuum called spacetime. This fabric is not a rigid stage upon which events unfold; it's active, flexible and responsive.
• Mass-Energy Warps Spacetime : Every speck of mass and every bit of energy in the universe distorts this spacetime fabric. The greater the mass or energy density, the more pronounced the curvature. This is akin to placing a bowling ball on a trampoline: it creates depression.
• Curved Spacetime Dictates Motion : Why do objects appear to be 'pulled' towards massive bodies? Because they are following the 'straightest possible paths' in this curved spacetime. If you roll a marble on the trampoline, it will naturally curve towards the depression created by the bowling ball. The marble isn't 'attracted' by a force from the bowling ball; it is simply following the contours of the warped surface. Similarly, Earth doesn't orbit the Sun because the Sun 'pulls' it; rather, Earth followed the geodesic in the spacetime curved by Sun's immense mass

This interplay means that gravity is not a force transmitted through space, but rather a property of space and time themselves.

The Language of Spacetime

To translate the intuition to precise scientific theory, Einstein employed the sophisticated and elegant mathematical framework of differential geometry.

Spacetime as a Manifold and the Metric Tensor (\(g_{\mu\nu}\))

The 4-dimensional spacetime is mathematically described as a differentiable manifold. This means that locally, it resembles flat Euclidean space, but globally, it can be curved. We used coordinates (\(x^0, x^1, x^2, x^3\)), where \(x^0 = ct\) (with \(c\) being the speed of light) is the time coordinate, and \(x^1, x^2, x^3\) are spatial coordinates.

In a curved spacetime, the concept of distance and time interval between two points becomes more complex than in flat space (Minkowski spacetime). The object that defines these measurements is the Metric Tensor (\(g_{\mu\nu}\)). The metric tensor acts like a ruler and a clock for spacetime. It exists at every point in spacetime and encapsulates all the information about how spacetime is curved in the vicinity of that point.

The infinitesimal spacetime interval \(\mathrm{d} s^2\) between two infinitesimally close spacetime points (\(x^0, x^1, x^2, x^3\)) and (\(x^0 + \mathrm{d} x^0, \cdots, x^3+ \mathrm{d} x^3\)) is defined as:

\[\mathrm{d} s^2 = g_{\mu\nu} \mathrm{d} x^{\mu} \mathrm{d} x^{\nu}\]

Here, \(\mu, \nu\) are indices ranging from 0 to 3, and the repeated indices imply summation according to the Einstein summation convention. In flat Minkowski spacetime, \(g_{\mu\nu}\) reduces to the Minkowski metric \(\eta_{\mu\nu}\)

\[\eta_{\mu\nu} = \begin{bmatrix}
-1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}\]

So, in flat spacetime, \(ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2\). However, in the presence of mass and energy, \(g_{\mu\nu}\) takes on a more complex form, and this complex form precisely describes the curvature of spacetime. The metric tensor also defines the light cone structure at each point, determining causal relationships. The inverse metric, \(g^{\mu\nu}\), is also crucial for raising and lowering tensor indices.

Covariant Derivative and Christoffel Symbols (\(\Gamma^{\mu}_{\alpha\beta}\))

In a curved spacetime, the usual partial derivatives are insufficient for differentiating tensors because the basis vectors themselves change from point to point. The concept of a vector changes as you move it around a curved surface. To properly differentiate tensors, we use the covariant derivative (\(\nabla_{\mu}\)). The covariant derivative accounts for the change in the vector components and the change in the basis vectors due to curvature.

These symbols are not tensors themselves, but they are the connection coefficients that tell us how the coordinate system twists and turns as we move through curved spacetime. They are defined solely in terms of the metric tensor and its first derivatives:

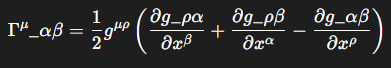
These symbols quantify how much a vector changes when it is parallel transported from one point to an infinitesimally nearby point.

Geodesics: The "Straightest" Paths

A freely moving particle (subject only to gravity) follows a geodesic in curved spacetime. A geodesic is the generalization of a “straight line” or the “shortest path” between two points in curved space. For instance, on Earth, the shortest path between two points is a great circle. Just as an airplane follows a great circle route, planets follow geodesics in the curved spacetime around the Sun.

The worldline of a particle following a geodesic is given by:

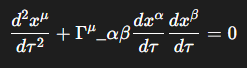
Here, $\tau$ is the proper time. This equation states that the acceleration of the particle is precisely balanced by the effects of spacetime curvature.

Curvature Tensors

To describe curvature quantitatively, we use curvature tensors:

• Riemann Curvature Tensor $R^{\rho}_{;\sigma\mu\nu}$: measures the failure of parallel transport. In flat space it vanishes, in curved space it does not. In 4D spacetime, it has 20 independent components.
• Ricci Tensor:
  $$
  R_{\mu\nu} = R^{\alpha}_{;\mu\alpha\nu}
  $$
• Ricci Scalar:
  $$
  R = g^{\mu\nu} R_{\mu\nu}
  $$

Stress–Energy Tensor $T_{\mu\nu}$

The stress–energy tensor encodes the distribution and flow of mass-energy:

$$
T_{\mu\nu} = \left( \rho + \frac{P}{c^2} \right) u_{\mu} u_{\nu} + P g_{\mu\nu}
$$

where $\rho$ is energy density, $P$ is pressure, and $u_{\mu}$ is the four-velocity of the fluid.

Conservation of energy and momentum:

$$
\nabla_{\mu} T^{\mu\nu} = 0
$$

Einstein Field Equations (EFE)

The Einstein Field Equations form the core of General Relativity:

$$
G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8 \pi G}{c^4} T_{\mu\nu}
$$

with Einstein tensor:

$$
G_{\mu\nu} = R_{\mu\nu} - \tfrac{1}{2} R g_{\mu\nu}.
$$

Here, $G_{\mu\nu}$ describes curvature, $\Lambda$ is the cosmological constant, $T_{\mu\nu}$ describes matter and energy, $G$ is Newton’s constant, and $c$ is the speed of light.

Physical Implications and Predictions

General Relativity not only explained phenomena that Newtonian gravity could not, but also made astonishing predictions that were later confirmed.

Precession of Mercury’s Perihelion

Mercury’s orbit precesses by about $43''$ per century beyond Newtonian prediction. General Relativity accounts for this precisely through spacetime curvature near the Sun.

Gravitational Lensing

Massive objects bend light by curving spacetime. This effect, gravitational lensing, was confirmed in 1919 during a solar eclipse. Today it is used to map dark matter, discover distant galaxies, and measure cosmic expansion. Iconic examples include the Einstein Cross.

Gravitational Redshift and Blueshift

Light escaping a gravitational well loses energy (redshift), while falling light gains energy (blueshift). Verified by the Pound–Rebka experiment (1959). GPS corrections rely on this effect; otherwise errors of ~10 km per day would occur.

Gravitational Waves

Accelerating masses generate ripples in spacetime: gravitational waves.

• Indirect evidence: Hulse–Taylor binary pulsar (1974), orbital decay matched GR predictions.
• Direct detection: LIGO (2015), observing black hole merger.

This opened a new window on the universe, allowing us to “hear” violent cosmic events.

Black Holes

Black holes are regions where gravity is so strong that nothing escapes beyond the event horizon.

• Form from collapsing massive stars.
• Contain a singularity where curvature diverges.
• Observed indirectly via stellar dynamics, and directly imaged by the Event Horizon Telescope (M87* and Sagittarius A*).

Cosmology

GR underlies modern cosmology:

• Solutions of EFE predict expanding/contracting universes (confirmed by Hubble).
• Friedmann equations describe cosmic expansion.
• GR supports the Big Bang model, explains cosmic evolution.
• Provides framework for dark matter and dark energy.

Challenges and Open Questions

Despite its success, GR leaves profound questions:

• Quantum Gravity: reconcile GR with quantum mechanics (string theory, loop quantum gravity).
• Singularities: breakdown points in black holes and Big Bang.
• Dark Matter/Energy: 95% of universe still unexplained.
• Information Paradox: does black hole evaporation destroy information?
• Cosmic Inflation: requires physics beyond GR.

Conclusion

General Relativity redefines gravity as geometry. Its elegant mathematics explains planetary motion, light bending, black holes, and cosmic expansion.

Yet it leaves mysteries — quantum gravity, dark matter, dark energy — ensuring it remains at the frontier of physics.

It is one of humanity’s greatest intellectual achievements: a beautiful tapestry of spacetime, where gravity is nothing but the dance of the cosmic fabric.