서론

케플러 법칙은 천체역학에서 가장 기본적이면서도 중요한 위치를 차지하고 있다. 이 글에서는 케플러의 3가지 행성운동법칙에 대해 알아보고 수식적으로 증명해 보도록 하겠다.

우주관의 역사

중세까지 널리 받아들여지던 프톨레마이오스식 우주관은 지구를 우주의 중심으로 놓고 천체의 완전한 원운동을 전제로 하였다. 주전원, 이심원을 도입하여 행성의 역행운동을 설명하였다. 그러나 행성의 운동이 지나치게 복잡히 기술되기도 하고, 측정의 발달로 기존 모델로는 설명하기 어려운 오차들이 발견되었고, 이는 우주를 다시 생각하게 만든 출발점이 되었다.

니콜라우스 코페르니쿠스(Nicolaus Copernicus, 1473–1543)는 우주의 법칙이 이렇게 복잡하지 않을 것이라는 믿음을 바탕으로 1542년 '천체의 회전에 관하여'를 통해 태양 중심 체계를 제안했다. 그의 모델은 지구를 포함한 여러 천체가 태양을 중심으로 돈다고 단순화하여 수학적으로 더 깔끔한 설명을 제공했다. 하지만, 코페르니쿠스의 모형도 문제가 있기는 했다. 코페르니쿠스는 우주에서 가장 자연스러운 운동은 등속 원운동이라고 생각하여 이를 그대로 적용하였다. 이는 오차를 발생시켰는데, 코페르니쿠스는 이 오차를 보정하기 위해 이심 등의 복잡한 개념을 다시 도입하였다.

티코 브라헤(Tycho Brahe, 1546–1601)는 정교한 관측을 통해 우주를 설계하였다. 티코 브라헤는 매우 뛰어난 관측 천문학자로 알려져 있다. (여담으로, 티코 브라헤는 시력이 엄청 좋았다고 한다. 1킬로미터 밖에서 동전이 500원짜리인지 100원짜리인지를 구별할 수 있을 정도였다는 이야기가 전해진다.) 브라헤도 처음에는 코페르니쿠스의 모형에 관심을 가졌으나, 태양 중심 모형의 근거가 되는 연주시차 관측 실패 등으로 인하여 태양 중심 모형이 틀리다는 결론을 내리고 새로운 태양계 모형을 발표하였다. 브라헤의 모델에 따르면, 지구를 제외한 모든 행성은 태양을 중심으로 공전하고, 달과 태양은 지구를 중심으로 공전한다.

요하네스 케플러(Johannes Kepler, 1571–1630)는 티코 브라헤의 조수 출신이다. 다만, 자신의 스승이 지구 중심 모형을 지지한 것과 반대로, 케플러는 태양 중심 모형에 매료되었다. 케플러는 브라헤의 정교한 관측 결과를 바탕으로 태양 중심 모형을 보완하고 행성 궤도에 대한 3가지 경험 법칙을 발견하였다. 케플러의 법칙들은 다음과 같다.

제 1법칙(타원 궤도 법칙): 행성은 태양을 하나의 초점으로 하는 타원궤도를 공전한다.

제 2법칙(면적 속도 일정 법칙): 행성과 태양을 잇는 가상의 선분은 같은 시간동안 같은 면적을 휩쓸고 지나간다.

제 3법칙(조화 법칙): 행성의 공전주기의 제곱은 행성 궤도 장반경의 세제곱에 비례한다.

케플러는 이 법칙들을 발견했으나 물리적으로 설명하지는 못했다. 이후 아이작 뉴턴(Isaac Newton, 1643-1727)이 중력 법칙, 미적분 등을 이용하여 수식적으로 증명하였다.

케플러 제 1법칙 증명

케플러 제 1법칙을 증명하는 방법에는 여러가지가 있다. Zeilik의 'Introductory Astronomy and Astrophysics' 등 천문학 교재에는 미분방정식을 이용한 증명을 다루는 경우가 많다. 하지만, 이 글에서는 미분방정식을 사용하지 않는 방식을 소개하도록 하겠다. (이 방식도 잘 알려져 있는 방식 중 하나이긴 하다.)

극좌표계 타원의 방정식

천체역학에서는 회전을 다루는 경우가 많아 극좌표계를 쓰는 것이 편리하다. 이 글에서도 주로 극좌표계를 이용할 것이다.

극좌표계에서의 타원의 방정식은 제 2 코사인 법칙을 이용하면 간단히 유도된다.

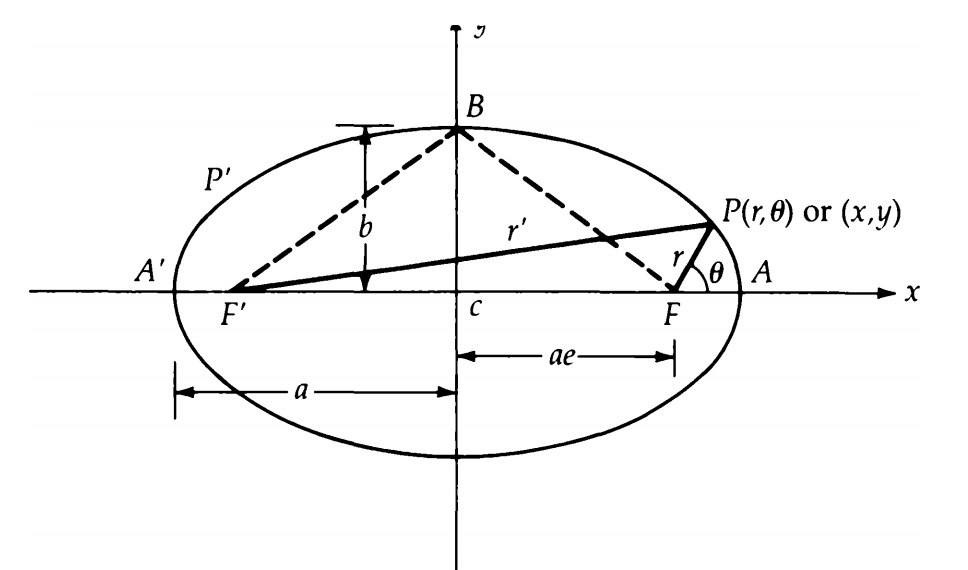
타원의 정의에 의해

\[r + r' = 2a,\quad r' = 2a - r\]

제 2 코사인 법칙에 의해
\[r'^2 = r^2 + (2ae)^2 - 2\cdot r\cdot(2ae)\cos(\pi-\theta) = r^2 + 4a^2 e^2 + 4 a e r \cos\theta\]\[(2a - r)^2 = r^2 + 4a^2 e^2 + 4 a e r \cos\theta\]\[4a^2 - 4 a r + r^2 = r^2 + 4 a^2 e^2 + 4 a e r \cos\theta\]\[4a^2 - 4 a r = 4 a^2 e^2 + 4 a e r \cos\theta\]\[a^2 - a r = a^2 e^2 + a e r \cos\theta\]\[a^2 (1 - e^2) = a r (1 + e \cos\theta)\]\[\displaystyle r=\dfrac{a(1-e^2)}{1+e\cos\theta}\]

이는 다음과 같이 나타내기도 한다.

\[r = \dfrac{l}{1 + e\cos\theta}\]

LRL 벡터를 활용한 증명

케플러 제 1법칙을 증명하기 위해 우선 한 벡터를 정의하자.
\[\mathbf R = \mathbf p \times \mathbf L - m k \hat{\mathbf r}\]

벡터 \(\mathbf R\)은 라플라스-룽게-렌츠 벡터(Laplace-Runge-Lenz vector, LRL vector)라고 불린다. (일반적으로는 \(\mathbf A\)를 쓰는 경우가 많지만, 케플러 제 2법칙에서 등장할 면적과 혼돈될 여지가 있다고 생각하여 이 글에서는 \(\mathbf R\)을 쓰도록 하겠다.) 식에 나오는 \(k\)는 중심력의 세기를 나타내는 수로, 이 경우 \(k=GMm\)이다. \(\mathbf R\)는 보존되는 것으로 알려져 있다.

\(\mathbf R\)가 보존된다는 것을 증명하기 위하여 \(\mathbf R\)를 시간에 대해 미분하자. (당연하게도, \(\mathbf R\)가 보존되면 \(\displaystyle\frac{d\mathbf R}{dt} = 0\)이다.)
\[\displaystyle\frac{d\mathbf R}{dt} = \frac{d}{dt}(\mathbf p \times \mathbf L) - m k \frac{d\hat{\mathbf r}}{dt}\]

우변의 첫째 항을 정리하자.
\[\displaystyle\frac{d}{dt}(\mathbf p \times \mathbf L) = \dot{\mathbf p} \times \mathbf L + \mathbf p \times \dot{\mathbf L}\]
각운동량 보존 법칙에 의해 \(\dot{\mathbf L} = 0\)이므로,

\[\displaystyle\frac{d}{dt}(\mathbf p \times \mathbf L) = \dot{\mathbf p} \times \mathbf L\]
중심력은 \(\dot{\mathbf p} = \mathbf F = -\dfrac{k}{r^2}\hat{\mathbf r}\)이므로,

\[\dot{\mathbf p} \times \mathbf L = -\dfrac{k}{r^2}\hat{\mathbf r} \times \mathbf L\]

위 식의 우변을 추가적으로 정리하자.
\[\hat{\mathbf r} \times \mathbf L = \hat{\mathbf r}\times m (\mathbf r\times\mathbf v)\]

벡터의 성질에 의해
\[\hat{\mathbf r} \times \mathbf L = m\hat{\mathbf r}\times(\mathbf r\times\mathbf v) = m\big(\mathbf r(\hat{\mathbf r}\cdot\mathbf v)-\mathbf v(\hat{\mathbf r}\cdot\mathbf r)\big)\]

\(\dot{r} = v_r = \mathbf v \cdot \hat{\mathbf r}\)이고, \(\dot{\mathbf r} = \mathbf v\) 이므로
\[\hat{\mathbf r} \times \mathbf L = m\big(r v_r\hat{\mathbf r}-r\mathbf v\big) \]

\[= -m r\big(\mathbf v - v_r\hat{\mathbf r}\big)\]
\[\dot{\mathbf p} \times \mathbf L = -\dfrac{k}{r^2}\big[-m r(\mathbf v - v_r\hat{\mathbf r})\big]\]\[= m k\dfrac{\mathbf v - v_r\hat{\mathbf r}}{r}\]
처음 미분식의 우변 둘째 항을 정리하자. r 방향 단위벡터의 미분은 다음과 같이 정리할 수 있다.

\[\frac{d\hat{\mathbf r}}{dt} = \frac{d}{dt} \left( \frac{\mathbf r}{r} \right) = \frac{\dot{\mathbf r}r - \mathbf r\dot{r}}{r^2} = \dfrac{1}{r}\big(\mathbf v - v_r\hat{\mathbf r}\big)\]

따라서, 처음 미분식의 우변 둘째 항은
\[m k\displaystyle\frac{d\hat{\mathbf r}}{dt} = m k\dfrac{\mathbf v - v_r\hat{\mathbf r}}{r}\]

결론적으로
\[\displaystyle\frac{d\mathbf R}{dt} = m k\dfrac{\mathbf v - v_r\hat{\mathbf r}}{r} - m k\dfrac{\mathbf v - v_r\hat{\mathbf r}}{r} = \mathbf 0\]

따라서, \(\mathbf R\)은 보존된다.

이제 \(\mathbf R\)를 이용해서 행성 궤도가 타원형임을 증명해보겠다.
\[\mathbf R = \mathbf p\times\mathbf L - m k\hat{\mathbf r}\]

\(\mu \equiv \dfrac{k}{m}\)이라 하고, 단위 질량당 각운동량 \(\mathbf H \equiv \dfrac{\mathbf L}{m} = \mathbf r\times\mathbf v\)을 정의하자.

이를 바탕으로 이심률 벡터 \(\mathbf e\)를 정의하자. (이름이 이심률 벡터인 이유는 이 벡터의 크기가 이심률이기 때문이다.)
\[\mathbf e \equiv \dfrac{\mathbf R}{m k} = \dfrac{\mathbf v\times\mathbf H}{\mu} - \hat{\mathbf r}\]

이심률 벡터와 위치 벡터를 내적하면
\[\mathbf e\cdot\mathbf r = \left(\dfrac{\mathbf v\times\mathbf H}{\mu} - \hat{\mathbf r}\right)\cdot\mathbf r\]

벡터의 성질에 의해
\[(\mathbf v\times\mathbf H)\cdot\mathbf r = \mathbf H\cdot(\mathbf r\times\mathbf v) = H^2\]\[\hat{\mathbf r}\cdot\mathbf r = r\]

따라서
\[\mathbf e\cdot\mathbf r = \dfrac{H^2}{\mu} - r\]
\(\mathbf e\cdot\mathbf r = er\cos\theta\)이므로
\[er\cos\theta = \dfrac{H^2}{\mu} - r\]\[r(1 + e\cos\theta) = \dfrac{H^2}{\mu}\]\[r = \dfrac{H^2/\mu}{1 + e\cos\theta}\]

결론적으로, \(l \equiv \dfrac{H^2}{\mu}\)이라 하면
\[r = \dfrac{l}{1 + e\cos\theta}\]

이는 극좌표계에서 원뿔곡선의 식이다. 태양 주위를 지속적으로 도는 행성의 경우, \(0<e<1\)로 타원 궤도를 가진다.

케플러 제 2법칙 증명

\(\Delta \theta\)가 매우 작다면 \(\Delta A\)를 부채꼴로 근사할 수 있을 것이다. (또는 작은 삼각형으로도 근사할 수 있다. 결과는 같게 나온다.) 따라서, 미소면적 \(dA\)와 미소각도 \(d\theta\)에 대하여

\[dA = \frac{1}{2} r^2 d\theta\]

시간에 대하여 미분하면

\[\frac{dA}{dt} = \frac{1}{2} r^2 \frac{d\theta}{dt} = \frac{1}{2} r^2 \dot{\theta}\]

단위 질량당 각운동량 \(\mathbf H = \mathbf r \times \mathbf v\)이므로, 그 크기는 \(H=r^2 \dot{\theta}\)이다. 이를 이용해 위 식을 정리하면,

\[\frac{dA}{dt} = \frac{1}{2}H\]

각운동량 보존의 법칙에 따라 \(H=\text{const}\)이므로, 면적 속도 \(\frac{dA}{dt}\)는 일정하다.

케플러 제 3법칙 증명

케플러 제 1법칙을 증명할 때 다루었듯이, 극좌표계에서 타원의 방정식은 다음과 같이 나타낼 수 있다.

\[r=\dfrac{a(1-e^2)}{1+e\cos\theta}=\dfrac{l}{1+e\cos\theta}=\dfrac{H^2/\mu}{1+e\cos\theta}\]

따라서

\[a(1-e^2)=\dfrac{H^2}{\mu}\]

이심률의 정의는 다음과 같다.

\[e=\dfrac{c}{a}=\dfrac{\sqrt{a^2-b^2}}{a}\]

따라서

\[a^2 e^2 = a^2 - b^2\]\[a^2(1-e^2)=b^2\]\[a(1-e^2)=\dfrac{b^2}{a}\]

앞서 \(a(1-e^2)=\dfrac{H^2}{\mu}\)라 하였으므로

\[\dfrac{H^2}{\mu}=\dfrac{b^2}{a}\quad\Rightarrow\quad H^2=\dfrac{\mu b^2}{a}\]

케플러 제 2법칙은 다음과 같이 표현할 수 있다.

\[dA=\tfrac{1}{2}H dt\]

이를 완전한 공전주기에 대해 적분하면

\[\displaystyle\int_{\text{orbital ellipse}} dA=\tfrac{1}{2}H\int_0^P dt\]

타원의 면적은 \(\pi a b\)이므로

\[\pi a b=\tfrac{1}{2}H P\]

이를 \(P\)에 대하여 정리하면

\[P=\dfrac{2\pi a b}{H}\]

양변을 제곱하자.

\[P^2=\dfrac{4\pi^2 a^2 b^2}{H^2}=\dfrac{4\pi^2 a^2 b^2}{\big(\mu b^2/a\big)}=\dfrac{4\pi^2}{\mu}a^3\]

따라서

\(P^2=\dfrac{4\pi^2}{GM}a^3\)

결론적으로, 행성의 공전주기 \(P\)의 제곱은 궤도장반경 \(a\)의 세제곱에 비례한다.

결론

지금까지 케플러 법칙에 대해 알아보았다. 케플러가 발견한 행성운동에 관련한 법칙들은 인류가 우주를 이해하는 방식을 바꾸었다. 케플러 법칙은 행성의 궤도를 이해하는데 중요한 역할을 하며, 다른 천체역학의 법칙들의 기초가 된다.

참고문헌

Zeilik, M., & Gregory, S. A. (1997). Introductory astronomy and astrophysics (4th ed.). Cengage Learning.

Karttunen, H., Kröger, P., Oja, H., Poutanen, M., & Donner, K. J. (2017). Fundamental astronomy (6th ed.). Springer.

Goldstein, H., Poole, C. P., & Safko, J. L. (2002). Classical mechanics (3rd ed.). Addison-Wesley.