Maximum Likelihood Estimation & Cramer Rao Lower Bound

필자는 모두가 이 글을 이해할 수 있기를 희망한다. 따라서 고등학교 확통만 이해해도 이 글을 이해할 수 있도록, 상당히 나이브한 개념부터 소개하고 있다.
하지만 동시에, 누구든지 이 글로써 얻어가는게 있기를 바란다. 따라서 최대한 많은 정보를 넣었으니 초반에 아는 내용이 있다면 적당히 넘겨가면서 끝까지 읽어보도록 하자!

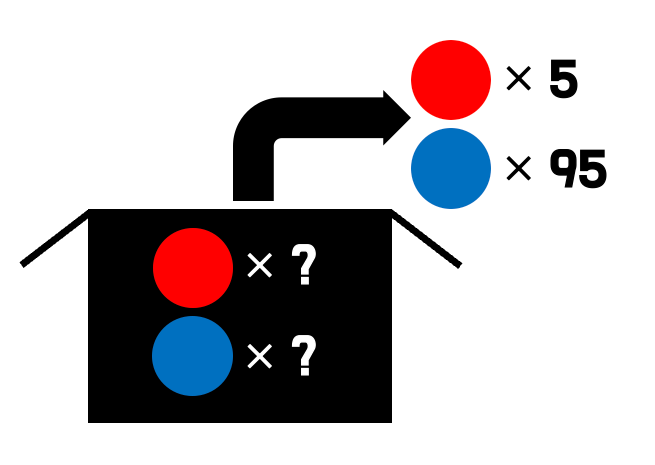
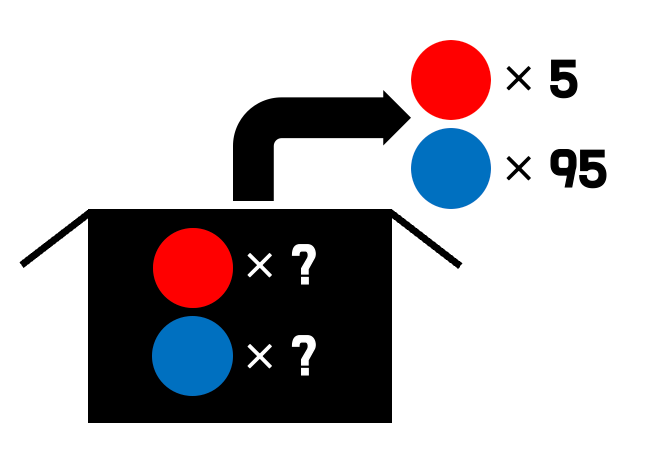
여기 빨간 공과 파란 공이 들어있는 불투명한 상자가 있다. 이 상자에서 공을 100번 뽑았는데, 빨간 공이 5번 나왔다고 해보자. 이 경우, 합리적으로 파란공이 빨간공에 비해 19배 많음을 추측할 수 있다.

이런 상황을 더 수학적으로 생각해보자.
편의 상 빨간 공이 나오는 상황을 1, 파란 공이 나오는 상황을 0에 대응시킨 확률변수 X를 생각하자. X에 대한 확률질량 함수는 아래와 같이 정의된다.

\[ P(x=k)= \begin{cases} \frac{n_R}{n_R+n_B}\quad \text{if k=1}\\ \frac{n_B}{n_R+n_B}\quad \text{if k=0} \end{cases}\]

\(\lambda\)를 \(\frac{n_B}{n_R}\)라 정의하면, \(X\sim Ber(\frac{1}{1+\lambda})\)라고 간단하게 표시할 수 있다(무슨 표기인지 모르겠다면 넘어가도 괜찮다. 궁금하다면 베르누이 분포를 찾아보자).
이런 수학적 상황에서 우리가 앞에서 한 짓은 \(Ber(\frac{1}{1+\lambda})\)를 따르는 i.i.d.한 100개의 확률변수 \(X_1, X_2, X_3...X_{100}\)을 통해서 확률분포의 parameter인 \(\lambda\)를 추정(estimate)한 것이다.

오늘 알아볼 것은 바로 추정 방법 중에 Likelihood라는 개념을 이용한 Maximum Likelihood Estimation(이하 MLE)과, MLE를 이용해 구한 추정량의 분산의 하한인 Cramer Rao Lower Bound(이하 CRLB)이다.

Likelihood

Likelihood의 개념을 설명하기 전에, 잠깐 추정 얘기로 돌아가보자.
첫번째 예시에서, 우리는 왜 \(\lambda\)가 19라고 추정하였을까? 다시 말해서 왜 19가 가장 그럴듯하다 생각하였을까? 굳이 수학적인 이유를 붙여본다면, \(\lambda\)가 19일 때 \(X\)의 기댓값이 0.05가 되기에 그렇게 판단한 것이다.
그런데 어쩌면, \(\lambda\)가 18인게 더 그럴 듯할수도 있지 않을까? 그냥 기댓값만으로 판단하는 건 논리적 완결성이 없는것 같다.

우리는 위와 같은 위험을 피하고자, parameter(\(\lambda\) 등) 별로 그럴듯한 정도를 수치화하고자 한다. 그리고 이 그럴듯한 정도를 Likelihood라고 한다.
확률적으로 접근하면 \(x\)(통계량)이 주어져 있을 때 파라미터 \(\lambda\)가 가질 확률로 서술할 수 있으므로, \(P(\lambda |x)\)로 쓸 수 있다. 이 때 일반적으로 \(L(\lambda)\)처럼, 함수 L로 Likelihood를 표기한다. 또한 L이 x에 매개함을 표시하기 위해 x도 변수로 넣기도 하지만, \(L\)이 \(x\)에 의해 정의되는 \(\lambda\)에 대한 함수임을 명시하기 위해 \(L(\lambda ;x)\)로 적는다. 머신러닝 등에서도 흔히 사용되는 표기법이므로 익숙해지면 좋다.

베이지안 확률론을 이용할 때 \(P(\lambda |x)\)를 다음과 같이 정리할 수 있다.
\[ P(\lambda |x) = \frac{P(\lambda) \cdot P(x|\lambda)}{P(x)}\]
이 때 \(x, \lambda\) 간 상관관계를 무시한 각각의 분포(주변확률분포)가 Uniform하다고 가정함으로써, \(P(x)\), \(P(\lambda)\)를 상수처리해서 \(P(\lambda |x)=C\cdot P(x|\lambda)\)로 쓸 수 있다.

위에서는 표기의 편의상 이산확률변수처럼 표기하였지만 \(X\), \(\Lambda\)가 연속확률변수일 때도 동일하게 작용한다. 이 경우 \(X\)의 확률밀도 함수 \(f(x; \lambda)\)에 대해 아래와 같이 Likelihood를 정리할 수 있다.
\[L(\lambda;x) = C \cdot f(x;\lambda)\]
C는 \(\lambda, x\)에 대해서도 모두 상수이고, 우리는 Likelihood를 \(\lambda\)간 비교에만 이용할 것이므로 상수 C를 제거해도 무방하다. 고로 아래와 같이 정리된다.
\[L(\lambda;x) = f(x;\lambda)\]

Maximum Likelihood Estimation

이제 위에서 구한 Likelihood를 최대화시키는 \(\lambda\)를 찾아보자. 그런데! 사소한 문제가 있다. 앞선 예시에서 복원추출을 100번 했던 것처럼, 일반적으로 여러개의 데이터를 사용하여 추정을 진행한다. 그런데 위에 식에서는 한개의 \(x\)에 대해서만 표기가 되어 있다. 이를 확장시켜, 여러 개의 데이터를 다루기 위해 Likelihood를 변형해보자.

기본적인 변형의 방향은 결합확률분포를 이용해 \(P(\lambda |x_1, x_2, ..., x_n)\)을 다루는 것이다. 결합 확률분포의 정의를 사용하면 아래와 같이 잘 정리할 수 있다.

\[
\begin{aligned}
P(\lambda | x_1, x_2, ..., x_n)
=\,&\frac{P(\lambda)}{P(x_1, x_2, ..., x_n)}\cdot P(x_1, x_2, ..., x_n| \lambda)\\
=\,&C \cdot P(x_1|\lambda)P(x_2|\lambda)...P(x_n|\lambda)
\end{aligned}
\]

두번째 줄로 넘어가는 과정에서 결합확률 분포를 분리하기 위해 각 변수가 독립임을 이용하였다 (i.i.d. assumption이용). \(P(x|\lambda) = L(\lambda; x)\)임을 이용해, 여러 확률변수에 대한 likelihood를 정리할 수 있다.

\[L(\lambda; x_1, x_2, ....x_n)=\prod_{i=1}^{n}L(\lambda ; x_i)\]

이제 정말 앞서 했던 추정을 수학적으로 표현할 수 있을 것 같다. 그런데 저렇게 Likelihood를 구했다면, 어떻게 최대화해야할까? 바로 미분이다! \(\lambda\)에 대해 Likelihood를 미분해서 0이 되는 점, 즉 극값을 찾은 후 Likelihood가 가장 큰 값을 찾으면 된다.
하지만 앞에서처럼 Likelihood가 여러 항의 곱으로 이루어져 있는데 그냥 미분을 하면 식이 매우 더러워질 것이다. 이런 상황을 피하기 위해 log를 씌운 뒤 미분을 해보자.
(이를 Log Likelihood라고 다른 개념처럼 부르기도 한다. 하지만 필자는 이거나 Likelihood나 동일한 개념이라 생각하며, 그냥 계산을 위해 이용하는 값이라 생각해 그렇게 중요하게 다루지 않는다. 사실 Likelihood보다 Log Likelihood를 더 일반적으로 사용한다.)

\[
\begin{aligned}
\text{Log Likelihood}
=&log L(\lambda; x_1, x_2, ...,x_n)\\
=&\sum_{i=1}^{n} log L(\lambda;x_i)
\end{aligned}
\]

MLE로 추정한 \(\lambda\)를 \(\hat{\lambda}\)로 표기할 때, \(\hat{\lambda}\)를 아래와 같이 정의할 수 있다.

\[\hat{\lambda} = \operatorname*{argmax}_{\lambda} \sum_{i=1}^{n} log L(\lambda;x_i)\]

MLE 해보기

이제 MLE에 대한 기초적인 지식을 모두 배웠다! 글의 시작에서 소개했던 예시로 MLE를 해 \(\lambda\)를 추정해보자.
우선 한 파일에 대한 Likelihood를 계산해보자. 수식 작성의 편의상 \(p=\frac{1}{1+\lambda}\)로 정의한다.

\[ P(x_1|p)= \begin{cases} p\quad &\text{if}\, x_1=1\\ 1-p\quad &\text{if}\, x_1=0 \end{cases}\]
\[
\begin{aligned}
L(p|x_1)=&P(x_1|p)\\
=&p^{x_1} \cdot (1-p)^{1-x_1}
\end{aligned}
\]

Likelihood에서 \(x_1\)에 대한 정의역을 {0, 1}로 한정할 때 위와 같이 \(P(x_1|p)\)를 간단하게 정의할 수 있고, Likelihood도 동일하게 정의된다. Log Likelihood도 비슷하게 간단하게 적용 가능하다.

\[
\begin{aligned}
log L(p|x_1, x_2, ...., x_n) =&\sum_{i=1}^{n} \{x_i\,log\,p+(1-x_i)\,log\,(1-p)\}\\
\hat{p}= \operatorname*{argmax}_{p}\sum_{i=1}^{n}& \{x_i\,log\,p+(1-x_i)\,log\,(1-p)\}\\
\frac{d}{d\hat{p}} \sum_{i=1}^{n} \{x_i\,log\,\hat{p}&+(1-x_i)\,log\,(1-\hat{p})\} = 0\\
=\left(\sum_{i=1}^{n}x_i\right)& \left(\frac{1}{\hat{p}} + \frac{1}{1-\hat{p}} \right) - n\frac{1}{1-\hat{p}}
\end{aligned}\]
\[
\begin{aligned}
\left( \sum_{i=1}^{n}x_i \right)\cdot&\left\{ \hat{p} + (1-\hat{p}) \right\} - n\cdot \hat{p} = 0\\
&\therefore \hat{p}=\frac{\sum_{i=1}^{n}x_i}{n}
\end{aligned}
\]

문제 상황으로 돌아가서, 총 100번 뽑아 빨간 공이 5번 나왔으니 \(n=100, \sum_{i=1}^{n}x_i=5\)이다. 그렇다면 위의 수식에 따라 우리는 \(\hat{p}=\frac{5}{100}\)이라 추정할 수 있고, \(\hat{p}=\frac{1}{1+\hat{\lambda}}\)이니 간단한 일차방정식을 풀면 \(\hat{\lambda}=19\)로, 우리가 직관적으로 추정한 값과 동일하다.

약간의 여담과 CRLB

위 결과만 본다면, 약간의 회의감이 들 수 있다. 열심히 열심히 미분해서 계산했는데, 고작 우리의 직관과 동일한 결과를 얻었으니 말이다. 하지만 직관으로 추측할 때와 달리 이렇게 MLE로 추정할 경우 얻을 수 있는 두 가지 장점이 있다.

첫번째로, 검증 가능하다. 결국 추정이라는 것은 iid하게 뽑은 확률변수로 parameter를 추측하는 것이다. 그럼 결국 추정값은 확률변수에 의존하는 값, 간단히 말해 확률변수이다. 그렇다면, 실제 \(\lambda\)가 1이었는데 극악의 확률로 100번 중 5개만 빨간공이었을 수도 있지 않을까? 이런 경우에 대응하고자 흔히 앞에서 말했듯이 추정량(estimator)의 분산을 구하곤 한다. 단순히 직관적으로 값을 추측한 것과 달리, MLE와 같은 수학적 방법으로 추정량의 분산을 구하기 용이하다. 이런 분산을 구하는 다양한 방법 중, 이번 글에서는 CRLB에 대해서 소개한다.

두번째로, 다변수 상황에 적용 가능하다. 방금은 parmaeter가 한 개여서 직관적으로 해결가능했지만, 만약 상자 안에 또 다른 상자가 있는 상황이었다면 어땠을까? 재귀적으로 상자를 여는 느낌의 상황말이다. 이런 상황에서는 직관적으로 답을 구하기 불가능하지만, 수식적인 방법을 활용해 열심히 계산하면 parameter를 추정할 수 있을 것이다.
여담으로, 인공지능도 여러 개의 파라미터에 대한 추정기이다. 물론 MLE보다 약간 고능한 방식이지만 CRLB는 애초에 보편적인 추정기에 적용 가능하므로 CRLB를 활용한 인공지능 성능 분석법도 존재한다. 물론 주류는 아니지만, 이렇게 확장이 가능하다는 점을 알아줬으면 좋겠다.

얘기가 나온 김에 다변수 상황에 대해 약간 고찰을 해보자. 결국 다변수 상황이라는 것은 여기서 확률변수가 여러 개라는 것을 의미하는데, 이 경우 각 변수 간 상관관계를 모두 고려해야한다. 이런 이유와 표기 편의 상, 지금부터 이 글에서는 확률변수와 파라미터를 모두 행렬로 관리한다. 상관관계 저장과 행렬이 무슨 상관인지 모르겠다면 다음 챕터를 참고하자. 다음 챕터에서는 행렬과 관련된 상식들을 간단히 정리한다.

백터와 관련된 상식들

사실 이 부분을 다뤄야 될지 고민이 조금 있었다. 사실 행렬곱 정도는 다들 알지 않을까 싶긴 한데, 행렬 미분이나 백터의 분산을 다루는 김에 행렬곱 등도 간단히 다뤄보고자 한다. 아래 내용 모두 CRLB를 계산하는데 사용하니까 모두 알아두자.
행렬미분은 행 백터나 열 백터를 사용함에 따라 형태가 달라지는데 본 글에서는 열 백터를 사용한다. 다시 말해 백터가 n행 1열의 행렬처럼 거동한다.

행렬곱

행렬 \(\mathbf{A}, \mathbf{B}\)에 대해 \(\mathbf{A}\)가 \(n \times m\), \(\mathbf{B}\)가 \(m \times k\)꼴일 때 두 행렬 \(\mathbf{A}, \mathbf{B}\)간에 곱셈이 아래와 같이 정의된다.

\[
\begin{aligned}
\mathbb{R}^{n\times m} \times \mathbb{R}^{m \times k} &\rightarrow \mathbb{R}^{n \times k}\\
\mathbf{A} \times \mathbf{B} &\mapsto \mathbf{C}\\
c_{ij}&=\sum_{k=1}^{m} (A_{ik} B_{kj})\\
&=\mathbf{A}_{i,;} \cdot \mathbf{B}_{;,j}
\end{aligned}
\]

마지막 줄은 \(\mathbf{A}\)의 \(i\)번째 행과 \(\mathbf{B}\)의 j번째 열을 내적한다는 의미이다. 자명하게 위의 정의와 동일하지만, 때때로 아래와 같이 쓰기도 한다.

백터로 스칼라 미분

\(\mathbb{R}^n\)의 백터 \(\boldsymbol{\theta}\)와 그에 매개하는 스칼라 \(a\)에 대해 \(\boldsymbol{\theta}\)에 대한 \(a\)의 미분이 아래와 같이 정의되며, \(\nabla_\boldsymbol{\theta}a\) 혹은 \(\frac{\partial}{\partial \boldsymbol{\theta}}a\)로 표기한다. 흔히 물리, 수학, 정보 등에서 사용하는 그래디언트와 동일한, 백터의 각 원소로 스칼라를 미분한 형태이다. 실제로 그래디언트라고 부른다.

\[
\begin{aligned}
\boldsymbol{\theta} \in \mathbb{R}^n&\quad \boldsymbol{\theta} = \begin{pmatrix} \theta_1\\ \theta_2 \\ \theta_3 \\ ... \\ \theta_n\end{pmatrix}
\\
\nabla_\boldsymbol{\theta}a \in \mathbb{R}^n & \quad \nabla_\boldsymbol{\theta}a = \begin{pmatrix} \frac{\partial}{\partial \theta_1}a \\ \frac{\partial}{\partial \theta_2}a \\\frac{\partial}{\partial \theta_3}a \\ ... \\\frac{\partial}{\partial \theta_n}a \end{pmatrix}
\end{aligned}
\]

백터로 백터 미분

\(\mathbb{R}^n\)의 백터 \(\boldsymbol{\theta}\)와 그에 매개하는 \(\mathbb{R}^m\)의 백터 \(\mathbf{a}\)에 대해 \(\boldsymbol{\theta}\)에 대한 \(\mathbf{a}\)의 미분이 아래와 같이 정의되며, \(\nabla_\boldsymbol{\theta}\mathbf{a}\) 혹은 \(\frac{\partial}{\partial \boldsymbol{\theta}}\mathbf{a}\)로 표기한다. 흔히 물리, 수학, 정보 등에서 사용하는 야코비안 행렬과 같은 형태이며 야코비안이라 부른다. 즉, 각 행이 \(\mathbf{a}\)의 각 원소에 대한 그래디언트이다.

\[
\begin{aligned}
\boldsymbol{\theta} \in \mathbb{R}^n\quad \mathbf{a} \in \mathbb{R}^m &\quad \boldsymbol{\theta} = \begin{pmatrix} \theta_1\\ \theta_2 \\ \theta_3 \\ ... \\ \theta_n\end{pmatrix} \quad \mathbf{a}=\begin{pmatrix} a_1\\a_2\\a_3\\...\\a_m\end{pmatrix}
\\
\nabla_\boldsymbol{\theta}\mathbf{a} &=\mathbf{B} \in \mathbb{R}^{m\times n}
\\
B_{ij}&=\frac{\partial}{\partial \theta_j}a_i
\\
B_{i,;}&=\frac{\partial}{\partial \boldsymbol{\theta}} a_i
\end{aligned}
\]
윗줄의 정의와 아랫줄의 정의가 자명하게 동일하지만, 윗줄의 정의가 보다 나이브한 정의이고 아랫줄의 정의가 이해하기 좋아서 둘 다 적어놓았다.

다른 예시로, \(\mathbf{a}\)가 \(\nabla_\boldsymbol{\theta}b\)인 경우 \(\nabla_\boldsymbol{\theta}\mathbf{a}\)를 \(\nabla_\boldsymbol{\theta}^2b\) 혹은 \(\frac{\partial^2}{\partial \boldsymbol{\theta}^2}b\)로 적을 수 있다.

공분산

사실 공분산(Covariance)은 행렬 관련된 내용은 아니고 통계쪽 내용이긴 하지만 그래도 알아놓자. 공분산은 두 개의 확률변수 \(X, Y\)의 선형관계에 대한 값으로, \(X\)가 평균보다 클 때 \(Y\)도 평균보다 크면 공분산의 값이 커지고 \(Y\)가 평균보다 작아지면 공분산의 값이 작아지도록 한다. \(X\)가 평균보다 작을 때도 같은 맥락으로 작동한다. 수식적으로는 아래와 같다.

\[
\begin{equation}
Cov(X, Y)=\mathbb{E}\left[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])\right]
\end{equation}
\]

참고로 확률변수 \(X\)의 분산은 \(Cov(X, X)\)와 같고 \(X, Y\)의 상관관계(피어슨 상관관계)는 \(Cov(X, Y)\)를 \(X, Y\)의 표준편차로 나눈 값이다.

나아가, 확률변수 백터 \(\mathbf{X}, \mathbf{Y}\)의 공분산도 아래와 같이 정의할 수 있다(확률변수 백터는 각 원소가 확률변수인 백터를 의미한다).

\[
\begin{aligned}
\mathbf{X} \in \mathbb{R}^n\quad \mathbf{Y} \in \mathbb{R}^m \quad \mathbf{X} &= \begin{pmatrix} X_1\\ X_2 \\ X_3 \\ ... \\ X_n\end{pmatrix} \quad \mathbf{Y}=\begin{pmatrix} Y_1\\Y_2\\Y_3\\...\\Y_m\end{pmatrix}
\\
Cov(\mathbf{X}, \mathbf{Y}) &\in \mathbb{R}^{n \times m}
\\
Cov(\mathbf{X}, \mathbf{Y})_{ij}&=Cov(X_i, Y_j)
\\
&=\mathbb{E}\left[(X_i-\mathbb{E}[X_i])(Y_j-\mathbb{E}[Y_j])\right]
\end{aligned}
\]

또한, 확률변수 백터를 아래와 같이 표현할 수 있다. 해당 내용은 적당히 자명해서(자명하진 않지만 정의로부터 손쉽게 증명 가능해서) 여기서 증명하지는 않고, 아래 Appendix로 남겨놓는다.

\[
\begin{equation}
Cov(\mathbf{X}, \mathbf{Y}) = \mathbb{E}\left[(\mathbf{X}-\mathbb{E}[\mathbf{X}])(\mathbf{Y}-\mathbb{E}[\mathbf{Y}])^T\right]
\end{equation}
\]

스칼라에서와 같이 확률변수 백터 \(\mathbf{X}\)의 분산은 공분산 \(Cov(\mathbf{X}, \mathbf{X})\)로 정의된다.

CRLB

드디어 본론이다. 사실 CRLB를 소개하고 싶은게 메인이라 앞 부분은 프롤로그이다. 기본적으로 \(\boldsymbol{\theta}_0\)이 실제 파라미터고, \(\hat{\boldsymbol{\theta}}\)가 MLE로 얻은 파라미터의 추정량이라고 할 때 \(\hat{\boldsymbol{\theta}}\)로 Likelihood를 미분한 값이 0인 것을 바탕으로 \( \hat{\boldsymbol{\theta}}-\boldsymbol{\theta}_0\)의 분포를 알아내는 것을 목표로 한다.

우선 적당히 필요한 변수부터 정확하게 명명하고 넘어가자. \(n\)번 반복 측정해서 얻은 데이터의 백터\(\mathbf{x}\), 해당 데이터로 계산한 Log Likelihood \(L_n(\boldsymbol{\theta})\), 해당 Log Likelihood로 추정한 파라미터를 \(\hat{\boldsymbol{\theta}}_n\)을 아래와 같이 정의하자. 단, 추후의 계산 편의 상 Log Likelihood에 상수 \(\frac{1}{n}\)을 곱하자.

\[
\begin{aligned}
&\mathbf{x} \in \mathbb{R}^n\quad \mathbf{x} =\begin{pmatrix} x_1\\ x_2\\ x_3 \\ ... \\ x_n\end{pmatrix}
\\
&L_n(\boldsymbol{\theta})=\frac{1}{n}\sum_{i=1}^{n} log L(\boldsymbol{\theta};x_i)
\\
&\hat{\boldsymbol{\theta}}_n = \operatorname*{argmax}_{\boldsymbol{\theta} \in \mathbb{R}^n} L_n(\boldsymbol{\theta})
\end{aligned}
\]

이 때 \(\nabla_\boldsymbol{\theta} L_n(\hat{\boldsymbol{\theta}}_n)=0\)임을 이용해 \(\hat{\boldsymbol{\theta}}_n-\boldsymbol{\theta}_0\)임을 계산하기 위해 고차원 평균값 정리를 이용해볼 수 있다.

\[
\begin{aligned}
\exists t \in (0, 1), \,\tilde{\boldsymbol{\theta}}&=t\hat{\boldsymbol{\theta}}_n + (1-t)\boldsymbol{\theta}_0, s.t.
\\
\nabla_\tilde{\boldsymbol{\theta}}^2L_n(\tilde{\boldsymbol{\theta}})^T (\hat{\boldsymbol{\theta}}_n - \boldsymbol{\theta}_0)&= \nabla_{\hat{\boldsymbol{\theta}}_n}L_n(\hat{\boldsymbol{\theta}}_n) - \nabla_{\boldsymbol{\theta}_0}L_n(\boldsymbol{\theta}_0)
\\
&=-\nabla_{\boldsymbol{\theta}_0}L_n(\boldsymbol{\theta}_0)
\end{aligned}
\]

첫째줄은 우리가 아는 평균값 정리와 유사하지만, 왜 전치가 들어가고 저게 가능한지 의문이 들 수 있다. 하지만 이를 여기서 증명하면 너무 다른 얘기로 새기에, Appendix에서 서술한다. 첫째 줄에서 둘째 줄로 넘어가는 것은 \(\hat{\boldsymbol{\theta}}_n\)의 정의에 의해 자명하다.

이 때 \(\nabla_\tilde{\boldsymbol{\theta}}^2L_n(\tilde{\boldsymbol{\theta}})\)의 \(i\)행 \(j\)열의 원소는 \(\frac{\partial^2}{\partial \tilde{\theta}_i \tilde{\theta}_j}L_n(\tilde{\boldsymbol{\theta}})\)로, 편미분은 미분 순서가 상관 없으므로 \(j\)행 \(i\)열의 원소와 동일하다. 즉, 대칭행렬이고 \(\nabla_\tilde{\boldsymbol{\theta}}^2L_n(\tilde{\boldsymbol{\theta}})^T = \nabla_\tilde{\boldsymbol{\theta}}^2L_n(\tilde{\boldsymbol{\theta}})\)이다.

그러면 이제 \(\hat{\boldsymbol{\theta}}_n - \boldsymbol{\theta}_0\)을 아래와 같이 정리할 수 있다.

\[
\hat{\boldsymbol{\theta}}_n - \boldsymbol{\theta}_0 = -\left(\nabla_\tilde{\boldsymbol{\theta}}^2L_n(\tilde{\boldsymbol{\theta}})\right)^{-1}\nabla_{\boldsymbol{\theta}_0}L_n(\boldsymbol{\theta}_0)
\]

위 식에서 좌변을 정리하기 위해 \(\nabla_\boldsymbol{\theta}L_n(\boldsymbol{\theta}_0)\)의 분포를 계산하고, \(\nabla_\boldsymbol{\theta}^2L_n(\tilde{\boldsymbol{\theta}})\)의 수렴값을 계산해 궁극적으로 \(\hat{\boldsymbol{\theta}}_n-\boldsymbol{\theta}_0\)의 분포 및 분산의 하한을 구한다.
(\(\nabla\)및에 첨자로 있는 \(\boldsymbol{\theta}\)는 편의 상 \(\boldsymbol{\theta}\)로 통일한다. 적당히 안에 있는 값에 따라 \(\hat{\boldsymbol{\theta}}_n\), \(\tilde{\boldsymbol{\theta}}\) 등으로 잘 해석하자.)

STEP1. \(\nabla_\boldsymbol{\theta} L_n(\boldsymbol{\theta}_0)\)의 분포 계산

우선 \(L_n(\boldsymbol{\theta})\)의 정의를 이용해서 \(\nabla_\boldsymbol{\theta} L_n(\boldsymbol{\theta}_0)\)를 조금 더 예쁘게 정리해보자.

\[
\begin{aligned}
\nabla_\boldsymbol{\theta} L_n(\boldsymbol{\theta}_0) & =\nabla_\boldsymbol{\theta}\frac{1}{n}\sum_{i=1}^{n}log L(\boldsymbol{\theta}_0;x_i)
\\
&=\frac{1}{n}\sum_{i=1}^{n} \nabla_\boldsymbol{\theta} log f(x_i;\boldsymbol{\theta}_0)
\end{aligned}
\]

마지막 식에서는 사실 \(\boldsymbol{\theta}_0\)이 상수이고 \(x_i\)에 매개하기에 Likelihood가 아니라 확률밀도 함수 f를 이용해 표기하였다.
그러면 위 식을 \(\nabla_\boldsymbol{\theta} log f(x_i; \boldsymbol{\theta})\)를 반복 측정하여 평균낸 값으로 해석할 수 있는데, n이 충분히 크다는 전제 하에 중심극한 정리를 이용해 \(\nabla_\boldsymbol{\theta}L_n(\boldsymbol{\theta}_0)\)의 분포를 구할 수 있다. 즉, 분포를 아래와 같이 정규분포로 근사할 수 있다.
\[
\nabla_\boldsymbol{\theta}L_n(\boldsymbol{\theta}_0) \sim \mathcal{N}(\mathbb{E}_X\left[\nabla_\boldsymbol{\theta}log f(x; \boldsymbol{\theta}_0)\right], \frac{1}{n}Var(\nabla_\boldsymbol{\theta}log f(x;\boldsymbol{\theta}_0))
\]

이제 \(\nabla_\boldsymbol{\theta} log f(x;\boldsymbol{\theta}_0\)의 평균과 분산을 구해보자. 식에서 첨자로 들어가 있는 \(X\)는 평균이 \(X\)에 대한 평균임을 의미한다. (x의 반복측정에 의한 중심극한 정리니 \(X\)에 의한 평균이 필요한 것이다.)

\[
\mathbb{E}\left[\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0)\right] =\mathbb{E}\left[\frac{\nabla_\theta f(x;\boldsymbol{\theta}_0)}{f(x; \boldsymbol{\theta}_0)}\right]
\]

널리 알려져 있는 로그함수의 미분공식을 쓰면 위와 같이 정리할 수 있다. 하지만 사실 우리는 로그함수의 미분을 스칼라 미분에서만 알고 있으니, 여기서도 사용 가능한지는 상당히 모호하다. 다만 이것도 여기서 증명하기에는 내용이 다른 곳으로 새니, 로그함수의 그래디언트에 대한 유도도 Appendix에서 진행한다.

\[
\begin{aligned}
\mathbb{E}\left[\frac{\nabla_\theta f(x;\boldsymbol{\theta}_0)}{f(x; \boldsymbol{\theta}_0)}\right] &=\int \frac{\nabla_ \boldsymbol{\theta}f(x; \boldsymbol{\theta}_0)}{f(x; \boldsymbol{\theta}_0)} f(x; \boldsymbol{\theta}_0) dx
\\
&=\int \nabla_\boldsymbol{\theta} f(x; \boldsymbol{\theta}_0) dx
\\
&=\nabla_\boldsymbol{\theta} \int f(x; \boldsymbol{\theta}_0) dx
\\
&=\nabla_\boldsymbol{\theta} 1 = 0
\end{aligned}
\]

첫번째 줄은 확률밀도 함수의 정의를 이용하였고, 둘째 줄에서 세번째 줄로 넘어간 것은 \(x\)에 대한 적분과 \(\boldsymbol{\theta}\)에 대한 미분이 순서가 상관 없음을 이용한 것이고, 네번째 줄로 넘어가는 것은 확률밀도 함수의 정규성을 이용한 것이다.

분산의 경우, 앞서 설명한 것처럼 공분산으로 구할 수 있는데 앞서 설명한(사실 뒤에서 Appendix에서 설명한) 수식아래와 같이 정리된다.

\[
\begin{aligned}
Var(\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0)) &= Cov(\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0), (\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0))
\\
&=\mathbb{E}\left[\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0)(\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0)^T\right]
\end{aligned}
\]

그런데 이 식은 널리 알려져 있듯이, 피셔 정보행렬(Fisher Information Matrix; \(\mathbf{I}(\boldsymbol{\theta}_0)\))이라 불리는 식이다.

그래서 요약하면 \(\nabla_\boldsymbol{\theta}L_n(\boldsymbol{\theta}_0)\)의 분포는 아래와 같이 표현된다.

\[
\nabla_\boldsymbol{\theta}L_n(\boldsymbol{\theta}_0) \sim \mathcal{N}(0, \frac{1}{n}\mathbf{I}(\boldsymbol{\theta}_0))
\]

STEP2. \(\nabla_\boldsymbol{\theta}^2L_n(\tilde{\boldsymbol{\theta}})\)의 수렴값 계산

우선 위 값의 수렴값을 계산하기 위해 \(\tilde{\boldsymbol{\theta}}\)가 \(\boldsymbol{\theta}_0\)로 수렴함을 보이고자 한다. 우선 이를 위한 보조정리로 \(\mathbb{E}\left[log f(x;\boldsymbol{\theta})\right]\)가 \(\boldsymbol{\theta} =\boldsymbol{\theta}_0\)에서 유일하게 최대임을 제시하고자 한다. 마음 같아서는 이 보조정리도 증명하거나 Appendix에서 보이고 싶지만, 이는 너무 긴 내용이라 이번 글에서 소개하기 어려울 거 같다. 궁금하다면 Shanon Entropy와 Mutual Entropy 사이의 Gibbs inequality에 대해 찾아보자. 기회가 되면 이 내용도 나중에 글로 정리해보겠다.
그래도 \(\boldsymbol{\theta}\)가 참값일 때 likelihood가 최대화되므로 \(\mathbb{E}\left[log f(x;\boldsymbol{\theta})\right]\)가 최소화되는 것을 직관적으로 납득하고 가자.

n이 충분히 클 때(발산할 때), \(L_n(\boldsymbol{\theta})\)는 \(\mathbb{E}[log f(x; \boldsymbol{\theta})]\)로 수렴한다(위 step1.과 동일한 방법). 이 때 \(\hat{\boldsymbol{\theta}}_n\)은 \(L_n(\boldsymbol{\theta})\)를 최대화시키는 \(\boldsymbol{\theta}\)이다.
따라서 n이 충분히 클 때, \(\hat{\boldsymbol{\theta}}_n\)을 \(\operatorname*{argmax}_{\boldsymbol{\theta}} \mathbb{E}\left[log f(x; \boldsymbol{\theta})\right]\)로 근사할 수 있다. 이 때 앞선 Gibbs Inequality에 의해 이 값은 \(\boldsymbol{\theta}_0\)으로 수렴한다.

즉, \(\hat{\boldsymbol{\theta}}_n\)은 \(\boldsymbol{\theta}_0\)으로 수렴한다. 사실 분산에 대해 얘기하는데 이렇게 수렴성으로 퉁치는게 괜찮은지 의문이 들 수 있다. 하지만 기본적으로 중심극한 정리에 의해 추정량의 분산이 0으로 가는 것은 당연한데 어느 정도 속도로 0으로 가는지 확인하고자 하는 것이기에 수렴성으로 논의하는 것이 괜찮다. 사실 이렇게 얘기해도 엄밀하지 않은 논증들이 있는데, 이는 분포 수렴과 확률 수렴을 구분하지 않고 서술했기에 그렇다. 이 역시 설명하자니 너무 길어져서 뭉뚱그려 썼는데, 나중에 기회가 된다면 이에 대해서도 정리해보겠다.

여차저차 말이 많았지만, 요약하자면 \(\hat{\boldsymbol{\theta}}_n\)은 \(\boldsymbol{\theta}_0\)으로 수렴한다. 그래서 궁극적으로 \(\nabla_\boldsymbol{\theta}^2L_n(\tilde{\boldsymbol{\theta}})\)의 수렴은 \(\nabla_\boldsymbol{\theta}^2L_n(\boldsymbol{\theta}_0)\)의 수렴 및 \(\nabla_\boldsymbol{\theta}^2\mathbb{E}\left[log f(x; \boldsymbol{\theta}_0)\right]\)의 수렴과 동일하다.

\[
\begin{aligned}
\nabla_\boldsymbol{\theta}^2 L_n(\tilde{\boldsymbol{\theta}}) &\rightarrow \nabla_\boldsymbol{\theta}^2 \mathbb{E}\left[log f(x; \boldsymbol{\theta}_0)\right]
\\
&=\mathbb{E}\left[\nabla_\boldsymbol{\theta}^2 log f(x; \boldsymbol{\theta}_0) \right]
\\
&=\mathbb{E}\left[\nabla_\boldsymbol{\theta}\left( \frac{\nabla_\boldsymbol{\theta}f(x; \boldsymbol{\theta}_0)}{f(x; \boldsymbol{\theta}_0)}\right) \right]
\\
&=\mathbb{E}\left[\frac{f(x;\boldsymbol{\theta}_0)\nabla_\boldsymbol{\theta}^2 f(x; \boldsymbol{\theta}_0) - \nabla_\boldsymbol{\theta}f(x; \boldsymbol{\theta}_0)\left(\nabla_\boldsymbol{\theta} f(x;\boldsymbol{\theta}_0)\right)^T}{\left(f(x; \boldsymbol{\theta}_0)\right)^2}\right]
\end{aligned}
\]

둘째줄에서 셋째줄로 넘어가는 건 앞서 설명한 로그함수의 백터 미분법칙을 이용한 것이고, 셋째 줄에서 넷째 줄로 넘어가는 것은 분수함수의 백터 미분법칙을 이용한 것이다. 둘 모두 우리가 스칼라 미분법칙에서만 아는 내용이므로 Appendix에서 세부적으로 증명한다.

\[
\begin{aligned}
&\mathbb{E}\left[\frac{f(x;\boldsymbol{\theta}_0)\nabla_\boldsymbol{\theta}^2 f(x; \boldsymbol{\theta}_0) - \nabla_\boldsymbol{\theta}f(x; \boldsymbol{\theta}_0)\left(\nabla_\boldsymbol{\theta} f(x;\boldsymbol{\theta}_0)\right)^T}{\left(f(x; \boldsymbol{\theta}_0)\right)^2}\right]
\\
&= \mathbb{E}\left[\frac{\nabla_\boldsymbol{\theta}^2 f(x; \boldsymbol{\theta}_0) }{f(x; \boldsymbol{\theta}_0 )}\right] -\mathbb{E}\left[\left(\frac{\nabla_\boldsymbol{\theta} f(x; \boldsymbol{\theta}_0) }{f(x; \boldsymbol{\theta}_0)}\right)\left(\frac{ \nabla_\boldsymbol{\theta} f(x; \boldsymbol{\theta}_0 }{f(x; \boldsymbol{\theta} _0)}\right)^T\right]
\\
&=\int \frac{\nabla_\boldsymbol{\theta}^2 f(x; \boldsymbol{\theta}_0)}{f(x; \boldsymbol{\theta}_0)} f(x; \boldsymbol{\theta}_0) dx - \mathbb{E}\left[\left(\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0)\right)\left(\nabla_\boldsymbol{\theta} log f(x; \boldsymbol{\theta}_0) \right)^T\right]
\\
&=\nabla_\boldsymbol{\theta}^2 1 - \mathbf{I}(\boldsymbol{\theta}_0) = -\mathbf{I}(\boldsymbol{\theta}_0)
\end{aligned}
\]

둘째 줄에서 첫번째 항은 step1.의 증명과 같이 적분에서 \(\boldsymbol{\theta}\)로의 미분을 밖으로 빼냄으로써 확률밀도함수의 정규화를 이용해 계산한 것이고, 두번째 항은 로그함수의 그래디언트를 이용해 치환한 다음 피셔 정보 행렬의 정의를 이용한 것이다.

결론적으로 \(\nabla_\boldsymbol{\theta}^2L_n(\tilde{\boldsymbol{\theta}})\)는 피셔 정보 행렬 \(\mathbf{I}(\boldsymbol{\theta}_0)\)에 대해 \(-\mathbf{I}(\boldsymbol{\theta}_0)\)로 수렴함을 알 수 있다.

STEP3. \(\hat{\boldsymbol{\theta}}_n - \boldsymbol{\theta}_0\)의 분포 및 분산 계산

이제 앞서 증명한 것들을 잘 묶어서 정리해보자. 일단 앞에서 증명한 세 가지 사실을 나열하면 아래와 같다.

\[
\begin{aligned}
\hat{\boldsymbol{\theta}}_n - \boldsymbol{\theta}_0 &= -\left(\nabla_\boldsymbol{\theta}^2 L_n(\tilde{\boldsymbol{\theta}})\right)^{-1}\nabla_\boldsymbol{\theta}L_n(\boldsymbol{\theta}_0)
\\
\nabla_\boldsymbol{\theta}L_n(\boldsymbol{\theta}_0) &\rightarrow \mathcal{N}(0, \frac{1}{n}\mathbf{I}(\boldsymbol{\theta}_0))
\\
\nabla_\boldsymbol{\theta}^2L_n(\tilde{\boldsymbol{\theta}}) &\rightarrow -\mathbf{I}(\boldsymbol{\theta}_0)
\end{aligned}
\]

위 세가지를 잘 묶으면 \(\hat{\boldsymbol{\theta}}_n-\boldsymbol{\theta}_0\)의 분포는 \( \mathcal{N}\left(0, (\mathbf{I}(\boldsymbol{\theta}_0)^{-1})^2 \cdot\frac{1}{n} \mathbf{I}(\boldsymbol{\theta}_0)\right) \), 즉 \(\mathcal{N}\left(0, \frac{1}{n}\mathbf{I}(\boldsymbol{\theta}_0) ^{-1}\right)\)가 됨을 알 수 있다. 다만, 이는 n이 매우 클 때의 수렴 분포이고 중간에 자연스럽게 넘어간 Gibbs inequality 등에 대해서 자세히 서술하면, 실제 분산은 \(\frac{1}{n}\mathbf{I}(\boldsymbol{\theta}_0)^{-1}\)이상임을 알 수 있다. 즉, \(\frac{1}{n}\mathbf{I}(\boldsymbol{\theta}_0)^{-1}\)가 MLE를 통해(사실 보편적인 추정을 통해) 구할 수 있는 추정량의 정밀도(분산)의 하한이다.

CRLB 구해보기

그래도 열심히 이론 전개를 했으니, 간단하게나마 활용을 해보자. 다변수 상황을 가져오기에는 계산이 너무 길어지니까, 그냥 처음에 예시로 제시했던 상황을 이용해보자.

우선 피셔 정보 행렬(여기서는 행렬이 아니라 스칼라긴 하다)은 아래와 같이 계산된다.
\[
\begin{aligned}
I(p)&=\mathbb{E}\left[\left(\frac{\partial}{\partial p}log f(x; p)\right)^2\right]
\\
&=p\cdot \left(\frac{\partial}{\partial p}log p\right)^2 + (1-p)\cdot \left(\frac{\partial}{\partial p}log(1-p)\right)^2
\\
&=p\cdot \frac{1}{p^2} + (1-p) \cdot \frac{1}{(1-p)^2}
\\
&=\frac{1}{p}+\frac{1}{1-p}=\frac{1}{p(1-p)}
\end{aligned}
\]

따라서 추정량 \(\hat{p}_n\)은 \(\mathcal{N}\left(0, \frac{p_0(1-p_0)}{n}\right)\)의 분포를 가지게 되고, 오차범위(표준편차)를 \(\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)로 근사할 수 있게 된다.

정리

우리는 지금까지 기본적인 점추정 방법인 MLE와, 일반적인 추정에 대해 분산의 하한인 CRLB에 대해 알아보았다. 간단히 유도도 해보았지만, 중간에 Gibbs Inequality 등 생략한 부분이 많아서 아쉬움이 남는다. 해당 부분이 궁금하다면 Information Theory에서 Entropy/KL Divergence와 관련해서 찾아보도록 하자. 별개로 추정 자체에 흥미가 생겼다면 머신러닝에 대해서도 알아보면 좋을 것 같다! 기회가 된다면 해당 내용에 대해서도 정리해서 글을 써보겠다.

Appendix

Appendix1. 공분산 행렬 식 정리

\[
\text{W.T.S} \quad Cov(\mathbf{X}, \mathbf{Y}) =\mathbb{E}\left[(X-\mathbb{E}[\mathbf{X}])(Y-\mathbb{E}[\mathbf{Y}])^T\right]
\]
\[
\begin{align}
pf) &\text{Let.} \mathbf{x}=\mathbf{X}-\mathbb{E}[\mathbf{X}]\quad\mathbf{y}=\mathbf{Y}-\mathbb{E}[\mathbf{Y}]
\\
&\Rightarrow Cov(\mathbf{X}, \mathbf{Y})_{ij}=\mathbb{E}[x_i\cdot y_j]
\\
\mathbf{x}\mathbf{y}^T &=\begin{pmatrix} x_1 \\ x_2 \\x_3 \\... \\x_n\end{pmatrix} \begin{pmatrix}y_1 & y_2 & y_3 & ... & y_m\end{pmatrix}
\\
&=\begin{pmatrix}x_1 y_1 & x_2 y_1 & x_3 y_1 & & x_n y_1\\
x_1 y_2 & x_2 y_2 & x_3 y_2 &... & x_n y_2\\
x_1 y_3 & x_2 y_3 & x_3 y_3 & & x_n y_3\\
&...&&...&...\\
x_1 y_m & x_2 y_m & x_3 y_m &...& x_n y_m\\
\end{pmatrix}
\\
\\
&\Rightarrow (\mathbf{x}\mathbf{y}^T)_{ij} = x_i y_j
\\
&\Rightarrow Cov(\mathbf{X}, \mathbf{Y})_{ij} =\mathbb{E}[x_i\cdot y_j] = \mathbb{E}[(\mathbf{x}\mathbf{y}^T)_{ij}]
\\
&\qquad\qquad =\mathbb{E}\left[(\mathbf{X}-\mathbb{E}[\mathbf{X}])(\mathbf{Y}-\mathbb{E}[\mathbf{Y}])\right]_{ij} \qquad\blacksquare
\end{align}
\]

Appendix2. 고차원 평균값 정리

\[
\begin{align}
\text{W.T.S.} &\forall f:\mathbb{R}^n \rightarrow \mathbb{R}\quad \mathbf{a}, \mathbf{b} \in \mathbb{R}^n \quad s.t.
\\
&\forall t \in [0, 1] f(t\mathbf{a} + (1-t)\mathbf{b}) \text{ is continuous}
\\
&\forall t \in (0, 1) f(t\mathbf{a} + (1-t)\mathbf{b}) \text{ is differentiable,}
\\
\exists t \in (0, 1) \quad s.t. \quad&\mathbf{c}=t\mathbf{a}+(1-t)\mathbf{b},\quad \nabla f(\mathbf{c})^T (\mathbf{a}-\mathbf{b})=f(\mathbf{a})-f(\mathbf{b})
\end{align}
\]
\[
\begin{align}
pf) \text{Let. }& g:[0, 1] \rightarrow \mathbb{R}^n\quad g(t) = t\mathbf{a}+(1-t)\mathbf{b}
\\
& h:[0,1] \rightarrow \mathbb{R} \quad h=f \circ g
\\\\
h \text{ is } & \text{differentiable in } (0, 1) \text{and}\\
&\text{continuous in } [0, 1]
\\
\Rightarrow&\text{Using Mean Value Theorem for scalar, }\\
&\exists c, \quad s.t. \quad \in (0, 1) h'(c)=h(1)-h(0)=f(\mathbf{a})-f(\mathbf{b})
\\
h'(c)&=\frac{d}{dc}f(g(c))
\\
&=\sum_{i=1}^{n}\frac{\partial f(g(c))}{\partial g(c)_i} \frac{\partial g(c)_i}{c}
\\
&=\sum_{i=1}^n \left(\nabla f(g(c))\right)_i \frac{\partial}{\partial c}\left(c\cdot a_i + (1-c)\cdot b_i\right)
\\
&=\sum_{i=1}^n \left(\nabla f(g(c))\right)_i \left(a_i-b_i\right)
\\
&=\sum_{i=1}^n \left(\nabla f(g(c))\right)_i \left(\mathbf{a}-\mathbf{b}\right)_i = \left(\nabla f(g(c))\right)^T (\mathbf{a}-\mathbf{b}) \quad \blacksquare
\end{align}
\]

Appendix3.로그함수의 그래디언트

\[
\begin{align}
\text{W.T.S.}\quad \nabla log f(\mathbf{x}) = \frac{\nabla f(\mathbf{x})}{f(\mathbf{x})}
\end{align}
\]
\[
\begin{align}
pf)\quad \left(\nabla log f(\mathbf{x})\right)_i &=\frac{\partial}{\partial x_i} f(\mathbf{x})
\\
&=\frac{\partial log f(\mathbf{x})}{\partial f(\mathbf{x})} \frac{\partial f(\mathbf{x})}{\partial x_i}
\\
&=\frac{1}{f(\mathbf{x})} \left(\nabla_f(\mathbf{x})\right)_i
\\
&=\left(\frac{\nabla f(\mathbf{x})}{f(\mathbf{x})}\right)_i\qquad \blacksquare
\end{align}
\]

Appendix4.분수함수의 그래디언트

\[
\text{W.T.S.} \quad \nabla \frac{g(\mathbf{x})}{f(\mathbf{x})} = \frac{f(\mathbf{x})\nabla g(\mathbf{x}) - g(\mathbf{x})\nabla f(\mathbf{x})}{f(\mathbf{x})^2}
\]

\[
\begin{align}
pf)\quad \left(\nabla \frac{g(\mathbf{x})}{f(\mathbf{x})}\right)_i &=\frac{\partial}{\partial x_i}\frac{g(\mathbf{x})}{f(\mathbf{x})}
\\
&=\frac{\partial f(\mathbf{x})}{\partial x_i}\frac{\partial}{\partial f(\mathbf{x})}\frac{g(\mathbf{x})}{f(\mathbf{x})}+\frac{\partial g(\mathbf{x})}{\partial x_i}\frac{\partial}{\partial g(\mathbf{x})}\frac{g(\mathbf{x})}{f(\mathbf{x})}
\\
&=-\left(\nabla f(\mathbf{x})\right)_i\frac{g(\mathbf{x})}{f(\mathbf{x})^2} +\left(\nabla f(\mathbf{x})\right)_i \frac{1}{f(\mathbf{x})}
\\
&=\left(\frac{f(\mathbf{x})\nabla g(\mathbf{x}) - g(\mathbf{x})\nabla f(\mathbf{x})}{f(\mathbf{x})^2}\right)_i\qquad \blacksquare
\end{align}
\]