Sackur-Tetrode Equation

Introduction
우선... 제목에 써져 있는 이상한 등식에 대해서 더 알아보고 싶은 사람은 많이 존재하지 않을 것이다...하지만...저 등식은 한국과학영재학교의 물리학 및 실험1에서 나오는 몇몇 개념들과 연관 지을 수 있다...따라서 물리학 및 실험의 엔트로피 부분의 설명이 너무 간략하여 재미가 없었던 사람들은 이 글을 읽어보기를 바란다...(아무도 안 읽겠지...ㅜ)
먼저, 제목에 써져 있는 이상한 등식이 뭘 뜻하는지 알아보도록 하자.
: 고전적인 이상 기체의 절대 엔트로피를 나타내는 식
\[S = Nk_B \left[ \ln \left( \frac{V}{N} \left( \frac{4 \pi m U}{3 N h^2} \right)^{3/2} \right) + \frac{5}{2} \right]\]
여기서, \(S\) 는 엔트로피, \(N\) 은 입자의 수, \(k_B\) 는 볼츠만 상수, \(V\) 는 기체의 전체 부피, \(m\) 은 입자의 질량, \(U\) 는 내부의 총 에너지, \(h\) 는 플랑크 상수이다.
이제 이 밑의 글은 Sackur-Tetrode Equation 을 유도하는 내용이 될 것이다.(읽기 싫으면 그냥 이런게 있다 정도로만 이해하자...)
Proof
먼저 물리학 및 실험1을 수강 했거나 물리에 조금만 관심이 있다면,
\[S=k_B\ln\Omega\]
라는 식은 익숙할 것이다. 이때, \(\Omega\) 는 상태수를 뜻한다. 여기서 \(k_B\) 는 상수이기 때문에 여기서부터는 \(\Omega\) 를 구하는데 집중할 것이다.
고전적인 이상 기체는 3 차원에서 입자의 개수가 \(N\) 개 있을 때, 각각의 입자가 위치 \(\vec q_i\) 와 운동량 \(\vec p_i\) 를 가지기 때문에 \(6N\) 차원의 위상 공간에 나타낼 수 있다. (만약을 위한 참고 : 각 입자는 3개의 위치 좌표와 3개의 운동량 좌표를 가진다) 따라서 미분 부피 요소는,
\[\mathrm{d}\Gamma = \prod_{i=1}^{N} \mathrm{d}^3q_i\mathrm{d}^3p_i\]
양자역학적 관점에서, 각 미시 상태는 플랑크 상수 \(h\) 로 이산화된 위상 공간 셀에 대응되기 때문에 상태수를 구할때는 \(h^{3N}\) 으로 나누어 준다. 또한 각 입자는 구분이 되지 않으므로 \(N!\) 으로 나누어 준다. 따라서 미시 상태수 \(\Omega\) 는,
\[\Omega = \frac{1}{N! h^{3N}} \int_{\Gamma} \prod_{i=1}^{N} \mathrm{d}^3 q_i \mathrm{d}^3 p_i\]
이상 기체이므로 입자 간 상호작용이 없다. 따라서 위 식의 위치와 운동량 부분은 전혀 연관성이 없으므로 아래의 식처럼 위치 부분과 운동량 부분으로 나누어 나타낼 수 있다.
\[\Omega = \frac{1}{N! h^{3N}} \left( \int \prod_{i=1}^{N} \mathrm{d}^3 q_i \right) \left( \int \prod_{i=1}^{N} \mathrm{d}^3 p_i \right)\]
이제 위치 부분과 운동량 부분을 각각 구할 것이다.
1-위치
하나의 입자에 대해서 입자는 부피 \(V\) 인 공간을 자유롭게 이동할 수 있으므로,
\[\int \mathrm{d}^3 q_i = V\]
따라서 \(N\) 개의 입자에 대해서,
\[\int\prod_{i=1}^N \mathrm{d}^3 q_i = V^N\]
2-운동량
운동량 적분은 내부 에너지 제약 조건에 의해 제한된다. 단원자 이상 기체임을 가정하면, 총 내부 에너지는 운동에너지의 합으로 표현된다.
\[\sum_{i=1}^N\frac{{p_i^2}}{2m} = U\]
이때, \({p_i}^2 = {p_{i,x}}^2 + {p_{i,y}}^2 + {p_{i,z}}^2\) 이다. 운동량의 제곱이 나타나도록 식을 정리하면,
\[\sum_{i=1}^N {p_i}^2 = 2mU\]
여기서 반지름 \(R = \sqrt{2mU}\) 인 \(3N\) 차원 초구면(hypersphere)을 정의하여 근사를 통해 식을 풀어나갈 수 있다. Microcanonical Ensemble 의 경우 에너지가 정확히 \(U\) 인 상태를 고려하지만, 실제로 에너지 껍질의 \(U\) 와 \(U + \delta U\) 사이의 부피를 계산한다. 글로 써진 다음의 내용을 디랙 델타 함수를 사용하여 수식으로 표현하면,
\[\int \delta \left( \sum_{i=1}^{N} \frac{p_i^2}{2m} - U \right) \prod_{i=1}^{N} \mathrm{d}^3 p_i\]
위 수식으로 나타내어진 에너지 껍질의 미소 부피(\(R\) 에서 \(R+\mathrm{d}R\) 까지의 부피)는 반지름이 \(R\) 인 \(3N\) 차원 구의 표면적에 \(\mathrm{d}R\) 을 곱하여 얻을 수 있다. 이때 \(R = \sqrt{2mU}\) 이므로 \(\mathrm{d}R = \frac{m\mathrm{d}U}{\sqrt{2mU}}\). 따라서,
\[S_{3N}(R) \cdot \mathrm{d}R = \frac{2 \pi^{3N/2} (2mU)^{(3N - 1)/2}}{\Gamma(3N/2)} \cdot \frac{m \mathrm{d}U}{\sqrt{2mU}}\]
식을 정리하면 최종적으로,
\[\int \delta \left( \sum_{i=1}^{N} \frac{p_i^2}{2m} - U \right) \prod_{i=1}^{N} \mathrm{d}^3 p_i = S_{3N}(R) \cdot \mathrm{d}R = \frac{2^{3N/2} \pi^{3N/2} m^{3N/2} U^{(3N - 2)/2} \mathrm{d}U}{\Gamma(3N/2)}\]
이제 위치 적분과 운동량 적분을 결합하면,
\[\Omega = \frac{1}{N! h^{3N}} V^N \cdot \frac{2^{3N/2} \pi^{3N/2} m^{3N/2} U^{(3N - 2)/2} \mathrm{d}U}{\Gamma(3N/2)}\]
위의 식은 상태수를 이상 기체의 여러 상수들(\(N\), \(V\), \(m\), \(U\))로 나타낸 것이다. 이제 위의 식으로 나타내어진 상태수 \(\Omega\) 를 가장 기초가 되는 식 \(S = k_B\ln\Omega\) 에 대입하여 이상 기체의 엔트로피를 구해보자. 로그를 취하게 되면,
\[\ln \Omega = -\ln N! - 3N \ln h + N \ln V + \frac{3N}{2} \ln 2 + \frac{3N}{2} \ln \pi \\ + \frac{3N}{2} \ln m + \frac{(3N - 2)}{2} \ln U - \ln \Gamma\left(\frac{3N}{2}\right)\]
위의 식에서 \(\mathrm{d}U\) 는 무시해도 되는 항이므로 생략되었다. 이제 위의 식에서 Stirling's Approximation 을 적용하면,
\(\ln N! \approx N \ln N - N\)
\(\ln \Gamma\left(\frac{3N}{2}\right) \approx \frac{3N}{2} \ln \left(\frac{3N}{2}\right) - \frac{3N}{2}\)
\[\ln \Omega \approx -N \ln N + N - 3N \ln h + N \ln V + \frac{3N}{2} \ln 2 + \frac{3N}{2} \ln \pi \\ + \frac{3N}{2} \ln m + \frac{(3N - 2)}{2} \ln U - \frac{3N}{2} \ln \left(\frac{3N}{2}\right) + \frac{3N}{2}\]
이제 위 식을 Sackur-Tetrode Equation 의 형태로 바꾸면,
\[\ln \Omega \approx N \ln \left(\frac{V}{N}\right) + \frac{3N}{2} \ln \left(\frac{4\pi m U}{3N h^2}\right) + \frac{5N}{2}\]
식을 정리하여 위의 식의 형태로 만드는 도중 나오는 \(-\ln U\) 는 \(N\rightarrow\infty\) 일 때 무시할 수 있으므로 생략한다.
최종적으로, 이상기체의 엔트로피 \(S\) 는,
Conclusion
오랜만에 꽤 긴 글을 쓴 것 같다. 이전의 글들이 모두 단편적이고 간단한 개념과 증명만을 다루는 글이었다면, 이번 글은 글을 읽기 위해 알고 있어야 하는 지식도 많아야 하고 수식을 다루는데 있어서 익숙해야만 완전히 이해할 수 있는 글이었다. 따라서 이 글이 이해가 되지 않는다면, 더 쉽게 설명하는 글들을 인터넷에서 찾아보거나 이 글에서 사용된 개념들을 대략적으로 숙지하는 것이 좋을 것 같다. 솔직히 말해서 Sackur-Tetrode Equation의 증명을 알고 있을 필요는 없다. 하지만 이 식을 증명하는데 사용되는 여러 아이디어들이 재미있고 물리에서 꽤 많이 쓰이는 스킬들이므로 잘 알고 있다면 언젠가는 유용하게 쓰일 것이다. 이 재미없는 글을 끝까지 읽어준 사람들에게 매우 감사하다는 말을 전하면서 이 글을 마무리하겠다.



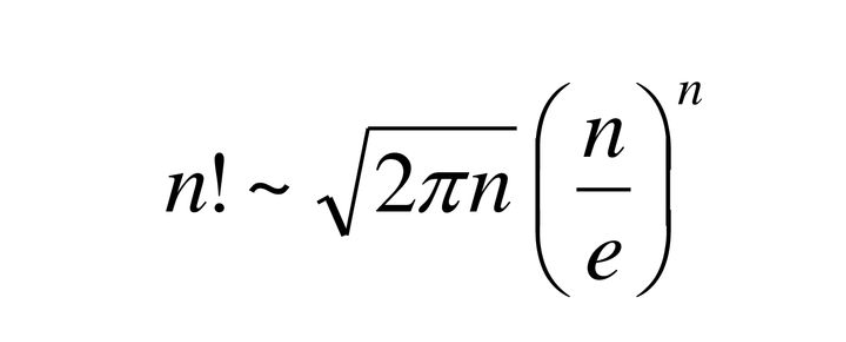









Comments ()