팩토리얼의 일반화는 왜 감마함수여야 하는가.
Math
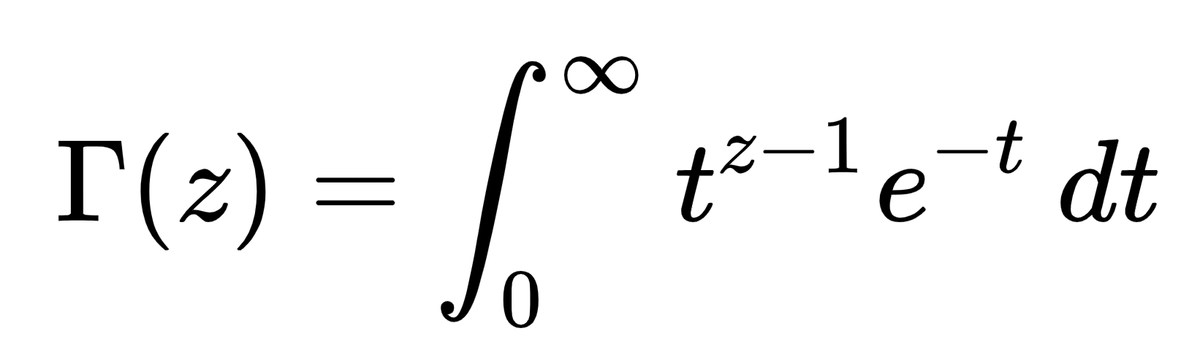
이 글은 박종휘씨의 추천으로 시작되었다.
현재 로지케이의 수학 글에서 감마함수를 팩토리얼과 동치로 사용하는 논의를 자주 이어갔다. 해당 글은 해당 논의에 적당한 정당성을 부여한다. 감마함수의 정당화 외에도 감마함수 자체를 더 깊이 이해할 수 있는 글이라 생각한다.
ㅤ
ㅤ
ㅤ
\[ \Gamma (n) = \int_{0}^{\infty} x^{n-1} e^{-x} dx = (n-1)! \,\,\,\,\,\,\,\, (n \in \mathbb{N})\]
이 만족하므로 적분이 수렴하는 \( \forall z \in \mathbb{C} \) 에 대해서
\[ \Gamma (z) = \int_{0}^{\infty} x^{z-1} e^{-x} dx = (z-1)! \]
라고 쓴다.
ㅤ
그러나 이러한 정의의 논리 전개 과정은 너무 부자연스럽다.
만약
\[ f : \mathbb{C} \to \mathbb{C} \,\,\, s.t. \, \forall n \in \mathbb{N} : f(n)=1 \]
을 잡으면 \( \Gamma (z) f(z) \) 도 팩토리얼을 일반화한 함수가 된다.
(이를테면, \(f(z) = \cos^2 (\pi z) \) 은 무한 번 미분 가능하기도 하다)
이때 \( f(z) =1 \)인 것은 어떻게 확신하는가? 그 경우가 가장 간단하기에 사용한다고 하면 그 이유는 무었인가? \( \Gamma (z) \) 보다 단순한 형태가 존재하지 않음을 증명할 수 있을까?
ㅤ
ㅤ
팩토리얼의 일반화를 분석하기 위해서는 이를 자연스럽게 확장할 수 있는 일반적인 성질이 필요하다. 먼저 \( (z-1)! = f(z) \) 를 만족하는 함수는 다음을 만족함은 팩토리얼 확장의 가장 기본적인 조건이다.
\[ z f(z) = f(z+1) \,\,\,\,\,\,\,\,\,\, (z \notin \mathbb{Z} ^{-} \cup \{ 0 \}) \]
이를 통해 팩토리얼을 직관적으로 표현함과 동시에 어떤 정수 \( n \)에 대해 \( (n, \, n+1) \)에서 \( f(z) \)를 정의하기만 하면 실수 전체 구간에서 \( f(z) \)가 정의된다는 사실을 알 수 있다.
다르게 말하면 위 조건만을 가지고는 팩토리얼의 정보와 실수 전체의 성질들을 통해 계승 함수를 특정할 수 없다.
ㅤ
팩토리얼의 성질을 알아보기 위해 이를 알아보기 쉬운 합의 형태로 바꾼다.
\[ \ln n! = \sum_{k=1} ^{n} \ln k \]
ㅤ
이때 \( n \)의 값이 커질 때마다 더해지는 \( \ln n \) 의 값도 커진다. 즉 \(\ln n! \) 은 \( n \)이 커질수록 빨리 증가한다. 이를 실수 전체로 확장하면 \(\ln x! \) 은 양의 실수를 정의역으로 할 때 아래로 볼록하다.
ㅤ
계승 함수 \( f(x) \)는 양의 실수에서 다음을 만족한다.
\[ \forall k \in [0,1] \,\, : \,\,\, \ln ( f(kx+(1-k)y)) \leq k \ln f(x) + (1-k) \ln f(y) \]
이 성질을 로그 볼록이라 한다.
ㅤ
로그 볼록을 활용하기 쉬운 식으로 변형하기 위해 함수 \( f(x) \) 에 대해 한 구간 \( (x_{1} , \, x_{2} ) \) (일단 대소 관계는 신경쓰지 말자) 에서 \( f(x) \)의 평균 변화율(기울기)을 \( D_{f(x)} (x_2 , \, x_1) \)로 정의하자.
\[ D_{f(x)} (x_2 , \, x_1) = \frac{ f(x_2 ) -f(x_1)} {x_2 - x_1} \]
이때 어떤 함수가 볼록이라 함은 \( D_{f(x)} (x_2 , \, x_1) \)이 \(x_1\)과 \(x_2\)에 대해 단조 증가라는 뜻이다. 직관적으로 잡는 구간이 오른쪽으로 갈수록 그 기울기는 커지는 것이다. 엄밀한 증명도 어렵지 않고 잘 알려져 있으니 넘어간다.
ㅤ
\(1. \, f(1) =0 \)
\(2. \, x f(x) = f(x+1) \)
\(3. \, \forall x_1 , \, x_2 \in \mathbb{R}^{+} \) : \( \,\,\, D_{ \ln f(x)} (x_2 , x_1) \)가 단조 증가이다.
ㅤ
계승함수의 유일성을 증명하기 위해 어떤 함수 \(f(x)\) 가 조건 1, 2를 만족할 때 조건 3을 만족하는 \( f(x) \) 가 존재함을 보이고 그 중 하나가 감마 함수의 적분 꼴임을 밝혀야 한다.
감마함수가 성질 1, 2 를 만족하는 것은 자명하므로 3번의 로그 볼록 성질을 만족함을 보인다.
\[ \forall k \in [0,1] \,\, : \,\,\, \ln ( \Gamma (kx+(1-k)y)) \leq k \ln \Gamma (x) + (1-k) \ln \Gamma (y) \]
을 보이기 위해 좌변에 적분식을 대입하고 꼴을 잘 변형하면
\begin{split}
\ln\left(\Gamma\left(kx+(1-k)y\right)\right) &=\ln\left(\int_{0}^{\infty}t^{kx+(1-k)y-1}e^{-t}dt\right)\\
&=\ln\left(\int_{0}^{\infty}t^{kx-k+(1-k)y-(1-k)}e^{-(kt+(1-k)t)}dt\right)\\
&=\ln\left(\int_{0}^{\infty}(t^{x-1}e^{-t})^{k}(t^{y-1}e^{-t})^{1-k}dt\right)\\
\end{split}
으로 식을 만들 수 있다.
ㅤ
이때 횔더 부등식,
\begin{split}
\int_a^b|f(x)g(x)|dx
\le\left(\int_a^b|f(x)|^pdx\right)^{1/p}\left(\int_a^b|g(x)|^qdx\right)^{1/q} \,\,\,\,\, ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, (\frac{1}{p}+\frac{1}{q}=1)
\end{split}
에 \( \dfrac{1}{p} = k \, , \,\, \dfrac{1}{q} =1-k \) 와 \( f(x) =( t^{x-1}e^{-t})^{k} \, , \,\, g(x) = (t^{y-1}e^{-t})^{1-k} \) 를 대입한다면 모양이 이쁘게 나온다.
ㅤ
\begin{split}
\ln\left(\Gamma\left(kx+(1-k)y\right)\right)
&=\ln\left(\int_{0}^{\infty}(t^{x-1}e^{-t})^{k}(t^{y-1}e^{-t})^{1-k}dt\right)\\
&\le\ln\left(\left(\int_{0}^{\infty}t^{x-1}e^{-t}dt\right)^{k}\left(\int_{0}^{\infty}t^{y-1}e^{-t}dt\right)^{1-k}\right)\\
&=k\ln\left(\int_{0}^{\infty}t^{x-1}e^{-t}dt\right)+(1-k)\ln\left(\int_{0}^{\infty}t^{y-1}e^{-t}dt\right)\\
&=k\ln\left(\Gamma(x)\right)+(1-k)\ln\left(\Gamma(y)\right)
\end{split}
ㅤ
곧
\[ \forall k \in [0,1] \,\, : \,\,\, \ln ( \Gamma (kx+(1-k)y)) \leq k \ln \Gamma (x) + (1-k) \ln \Gamma (y) \]
가 만족하므로 감마함수는 로그볼록이다.
위의 3 정리를 모두 만족하는 \( f(x) \) 가 존재함이 확인되었으니 유일성을 보이는 논리를 전개한다.
ㅤ
ㅤ
이제 우리는 \( D_{ \ln f(x)} (x_2 , \, x_1) \)가 단조 증가하는 것이 확인된 상태에서 이 함수가 유일함을 보이기 쉽도록 구간 \( (x_{1} , \, x_{2} ) \)를 적당히 잡아야 한다.
또 로그 볼록의 성질은 구간을 \( (n-1, \, n) \) 과 \( (n,\, n+1) \) 로 잡았을 때 각 구간에서의 변화율인 \( \ln n \) 과 \( \ln (n+1) \) 의 차인 \( \ln \left( 1 + \dfrac{1}{n} \right) \) 는 \(n\)의 값이 커질 수록 0에 가까워진다. 즉, 이 두 구간에서의 변화량의 차가 0으로 가까워지는 와중에 그 변화량들은 증가해야 하므로 큰 \(n\)에 대해 해당 로그 볼록 조건이 더 타이트해 진다고 추론한다.
즉, 로그 볼록 조건이 충분히 타이트하지 않은 초반에 함수를 결정해 조건 2를 사용해 오른쪽으로 이동하지 말고, 충분히 큰 자연수 \( n \) 의 근처에서 \( f(x) \)를 확정하고 이를 역으로 왼쪽으로 끌고오는 성질의 증명을 구상한다.
곧 \( \displaystyle \lim_{n \to \infty} \)인 상황에서 샌드위치 정리를 사용하는 계획을 세운다.
일단 두 정수 사이의 구간 내에서 잡은 임의의 실수에 대해 해당 성질을 적용하는 것이 적당해 보인다.
ㅤ
ㅤ
본격적인 증명에 앞서 위 2번 성질에 수학적 귀납법을 적용해 \( n \in \mathbb{N} \) 에 대해
\[ f(x+n) = (x+n-1)(x+n-2) \cdots (x+1)xf(x) \,\,\,\,\,\,\,\,\,\,\,\,\,\, (*) \]
를 얻고 시작한다.
ㅤ
어떤 큰 \( n \in \mathbb{N} \) 와 \( x \in (0, \, 1] \) 를 잡고
\[ D_{ \ln f(x) } (n-1 , \, n) \leq D_{ \ln f(x) } (n+x , \, n) \leq D_{ \ln f(x) } (n+1 , \, n) \]
을 세운다. 가장 오른쪽 \( x_2 \) 자리에 \( n \) 을 둘 수 없기 때문이다.
ㅤ
\[ \frac { \ln f(n-1) - \ln f(n)} {(n-1) - n} \leq \frac { \ln f(n+x) - \ln f(n)} {(n+x) - n} \leq \frac { \ln f(n+1) - \ln f(n)} {(n+1) - n} \]
ㅤ
\( f(n) = (n-1)! \) 을 이용하고 팩토리얼로 바꾸지 않는 \( \ln f(x+n) \)에 대해 정리하면
\[ \ln (n-1)! -\ln (n-2)! \leq \frac {\ln f(n+x) -\ln (n-1)!} {x} \leq \ln n! -\ln (n-1)! \]
ㅤ
\[ x \ln(n-1) \leq \ln f(n+x) -\ln ((n-1)!) \leq x \ln n \]
ㅤ
\[ \ln((n-1)^x (n-1)!) \leq \ln f(x+n) \leq \ln(n^x (n-1)!) \]
ㅤ
\( \ln \)은 증가 함수이므로
\[ (n-1)^x (n-1)! \leq f(x+n) \leq n^x (n-1)! \]
ㅤ
(*)를 이용하면
\[ \frac {(n-1)^x (n-1)!} {(x+n-1)(x+n-2) \cdots (x+1)x} \leq f(x) \leq \frac {n^x (n-1)!} {(x+n-1)(x+n-2) \cdots (x+1)x} \]
ㅤ
그러나 현재로서는 양쪽 분자의 지수의 밑이 달라 \( n \)을 무한대로 보내기에 곤란한 상황이 연출된다.
그런데 왼쪽과 오른쪽 부등호를 따로 생각한다면 \( f(x) \) 쪽은 \(n\)에 대해 독립이므로 \( n\)자리에 아무 자연수를 넣어도 된다. 즉 지수의 밑을 통일하기 위해 왼쪽 부등식에 \(n\) 대신 \(n+1\) 을 대입한다.
ㅤ
\[ \frac {n^x n!} {(x+n)(x+n-1) \cdots (x+1)x} \leq f(x) \leq \frac {n^x (n-1)!} {(x+n-1)(x+n-2) \cdots (x+1)x} \]
ㅤ
이제 양쪽에 비슷하게 생긴 \( \frac {n^x n!} {(x+n)(x+n-1) \cdots (x+1)x} \) 의 형태를 직접 일치하도록 변형한다.
ㅤ
\[ \frac {n^x n!} {(x+n)(x+n-1) \cdots (x+1)x} \leq f(x) \leq \frac {n^x n!} {(x+n)(x+n-1) \cdots (x+1)x} \, \cdot \frac{x+n}{n} \]
ㅤ
마지막으로 \( n \to \infty \)의 극한을 취하면 샌드위치 정리에 의해
ㅤ
\[ f(x) = \lim_{n \to \infty} \frac {n^x n!} {(x+n)(x+n-1) \cdots (x+1)x} \]
로서 유일하게 결정된다.
ㅤ
이 \( f(x) \)를 정리하면 다음의 형태가 나오는데,
\[ x f(x) = f(x+1) = \lim_{n \to \infty} n^x \prod_{k=1}^{n} \frac {k} {x+k} \]
은 가우스 극한, 오일러 극한 등으로 알려진 감마함수의 한 형태 중 하나로 이의 적분꼴과 동치임이 알려져 있다.
ㅤ
ㅤ
감마함수가 3개의 조건을 만족하고 그 조건들을 만족하는 함수가 유일함을 보였으니 감마함수가 유일한 정당한 팩토리얼의 일반화라고 할 수 있다.
ㅤ
ㅤ
ㅤ
위 논의를 통해 로그볼록을 비롯한 성질 3가지를 만족하는 함수는 감마함수로 유일함이 증명되었다.
이 논의는 한 성질을 만족하는 함수를 찾고 이를 만족하는 함수가 유일하나 알고 있던 것과 다를 때 이 둘은 동치임을 말한다. 즉 이러한 유일성의 증명은 감마함수의 적분꼴과 무한곱 꼴이 동치임을 증명한 것도 된다.
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
출처








Comments ()