시리즈 | Integration - 오늘의 적분 2

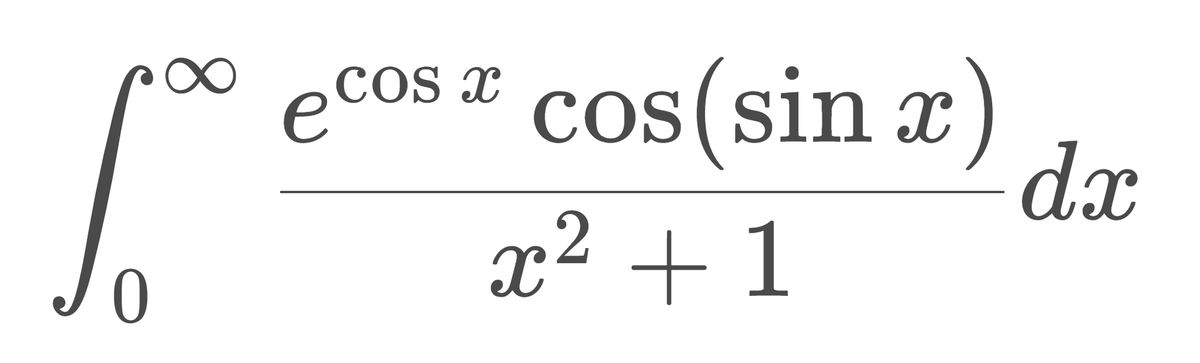
오늘이 적분은 작가 개인적으로 꽤 큰 의미를 가지고 있다. 일단 장영실 1차 합격 후 제출한 연구 증빙 자료에서 대부분의 분량을 차지한 적분 노트에서 첫 페이지를 담당하고 있는 적분이다. 그 말은 내가 대부분의 적분 기술을 익힌 채널 math 505 의 영상 중에서도 꽤 초반 부에 접한 영상이라는 뜻이다. 이러한 개인적인 사연 이외에도 해괴망측한 형태의 함수와 풀이에 사용되는 수 많은 테크닉은 이 적분 하나 만으로도 적분의 세계로 나아갈 때 좋은 첫 걸음이 될 수 있도록 만든다.

ㅤ

ㅤ

ㅤ

ㅤ

ㅤ

\[ I = \int_{0}^{\infty} \frac{e^{\cos x} \cos(\sin x)}{x^2 +1} dx \]

지수로 \( \cos x \) 가 위치해 있고 또 그 옆에는 \( \cos(\sin x) \) 라는 말도 안되는 항이 붙어 있다. 분수를 구성하는 \( \dfrac{1}{1+x^2} \) 은 혼자 있을 때 적분이 쉬우니 그나마 괜찮아 보이나 또 분자를 보면 그게 무슨 의미가 있나 싶다.

ㅤ

ㅤ

일단 차근차근 나아가기 위해 여러가지 생각을 해 볼 수가 있다.

1. 분자의 \( e^{\cos x} \) 과 \( \cos ( \sin x) \) 중 어떤 것을 먼저 변형해야 할까? 이상한 두 항이 붙어 있는 경우에는 왜 굳이 그 둘을 주었을까 생각하며 이를 한 번에 처리할 궁리를 먼저 한다.
2. \( e^{\cos x} \) 은 매클로린 급수로 전개했을 때 삼각 다항식이 나오나 뒤의 \( \cos ( \sin x) \) 와 잘 어울리지 않는다.

3. 그럼 \( \cos ( \sin x) \) 를

( \( e^{ix} = \cos x + i \sin x \) ) 에서 얻은 ( \( \cos x = \operatorname{Re}(e^{i x}) \) ) 의 꼴로 변형하면

\[ e^{\cos x} \cos ( \sin x) = \operatorname{Re}( e^{\cos x + i \sin x} )= \operatorname{Re} ( e^{e^{ix}}) \]

으로 변형하면 성공했다는 느낌이 든다.

\[ I = \int_{0}^{\infty} \frac{\operatorname{Re} ( e^{e^{ix}})}{x^2 +1} dx = \operatorname{Re} \int_{0}^{\infty} \frac{e^{e^{ix}}}{x^2 +1} dx\]

적분은 선형적 과정이므로 실수부 연산자의 분배 법칙이 성립한다는 사실을 알 수 있었다.

ㅤ

이제 \( e^{e^{ix}} \)를 처리해 주어야 한다. 그럼 분자에 남은 것도 없으니 매클로린 급수로 전개해보자. 또 매클로린 급수에서 k제곱을 하는 항이 \( e^{ix} \) 이므로 \( e^{kix} \) 로 좋은 형태가 된다.

\[ I = \operatorname{Re} \displaystyle \int_{0}^{\infty} \dfrac{\displaystyle \sum_{k=0}^{\infty} \frac{e^{ikx}}{k!} }{x^2 +1} dx \]

적분이 수렴한다는 가정하에 적분은 선형적이므로

\[ I = \operatorname{Re} \sum_{k=0}^{\infty} \frac{1}{k!} \int_{0}^{\infty} \frac {e^{ikx}}{1+x^2} dx \]

맨 앞에 \( \operatorname{Re} \)와 피적분 함수의 분자에 있는 \( e^{ikx}\) 가 결합한다!

\[ I = \sum_{k=0}^{\infty} \frac{1}{k!} \int_{0}^{\infty} \frac {\cos kx}{1+x^2} dx \]

ㅤ

이 상태에선 시그마 기호를 뺄 수 있음을 알 수 있다.

\( -1 \leq \cos kx \leq 1 \) 이고 \( \dfrac{1}{1+x^2} > 0 \) 이므로

\[ -\frac{1}{1+x^2} \leq \frac{\cos kx}{1+x^2} \leq \frac{1}{1+x^2} \]

\[ - \frac{\pi}{2} \leq \int_{0}^{\infty} \frac{\cos kx}{1+x^2} dx \leq \frac{\pi}{2} \]

\[ - \frac{\pi}{2} e \leq \sum_{k=0}^{\infty} \frac{1}{k!} \int_{0}^{\infty} \frac {\cos kx}{1+x^2} dx = I \leq \frac{\pi}{2} e \]

뭐 이런 식이다.

ㅤ

ㅤ

일단

\[ I_k = \int_{0}^{\infty} \frac {\cos kx}{1+x^2} dx \]

를 훨씬 간단한 문제로서 잡았다.

ㅤ

가장 먼저 생각나는 방법은

\[ \cos kx + i \sin kx = e^{ikx} = ( \cos x + i \sin x)^k = \sum_{n=0}^{k} \,_{k}C_{n} i^n \sin^n x \cos^{k-n} x\]

에서 얻는

\[ \cos kx = \sum_{0 \leq 2m \leq k} \,_{k}C_{2m} (-1)^m \sin^{2m} x \cos^{k-2m} x \]

라고 쓰더라도 \( \tan \) 로 바꿔 쓰는 경우나 어떻게 바꾸든 분모와 잘 어울리지 않는 듯하다. \( \dfrac{1}{1+x^2} \) 은 \( x= \tan \theta \) 로 치환하는데 이미 \( x\)가 각이기 때문이다.

ㅤ

ㅤ

이런 경우에서 사용하는 방법이 바로 Feynman integration trick; differentiating under the integral sign 이다.

어떤 다변수 함수를 적분하는 과정에서 \( f \) 가 미분 가능하다면

\[ I'(z) = \frac{d}{dz} \int_{a}^{b} f(x, \, z) dx = \int_{a}^{b} \frac{\partial}{\partial z} f(x , \, z) dx\]

에서 \( \frac{\partial}{\partial z} f(x , \, z) \) 가 적분하기 쉽거나 이전과 반복되는 형태일 때, 또 이런 \( I'(z) \) 가 적분하기 쉬운 형태일 때 유용하다.

ㅤ

일단 함수를 미분하기 위해 \( I_k = I(a) \) 로 변수를 실수로 확장한다. 그리고 간절히 기도한다.

\begin{equation*}
\begin{split}
I'(a)&=\frac{d}{da}\int_{0}^{\infty}\frac{\cos ax}{1+x^2}dx\\[1.5ex]
&=\int_{0}^{\infty}\frac{\partial}{\partial a}\frac{\cos ax}{1+x^2}dx\\[1.5ex]
&=-\int_{0}^{\infty}\frac{x\sin ax}{1+x^2}dx
\end{split}
\end{equation*}

이 때 처음 변수로 사용한 \( k \) 가 자연수, 즉 양수이므로 \( I(a) \)또한 양의 실수에서 정의된 함수라고 생각한다. 이는 나중에 이 함수의 미분값을 구할 때 중요하게 사용된다. 즉 초기값으로 사용하는 \( a=0 \) 은 \( \displaystyle \lim_{a \to 0^+} \)의 경우로 본다.

ㅤ

한 번의 미분 까지는 아직 별로 진전한 것 같이 보이지 않는다. 그런데 여기서 한 번 더 미분한다면 분자의 삼각 함수가 다시 \( \cos \) 이 되고 그 앞의 항이 \( x^2 \) 가 되어 분모와 작동할 수 있다.

\begin{equation*}
\begin{split}
I''(a)&= - \frac{d}{da}\int_{0}^{\infty}\frac{x \sin ax}{1+x^2}dx\\[1.5ex]
&=- \int_{0}^{\infty}\frac{x^2 \cos ax}{1+x^2}dx\\[1.5ex]
&=-\int_{0}^{\infty}\frac{(x^2 +1 -1) \cos ax}{1+x^2}dx\\[1.5ex]
&= -\int_{0}^{\infty}\cos ax - \frac{1}{1+x^2} dx
\end{split}
\end{equation*}

그러나 이 때는 앞의 \( \cos ax \) 의 특이적분이 수렴하지 않는다. 그러니 바로 한 번 더 미분하는 것은 적절하지 않다는 사실을 알고간다.

ㅤ

일단 앞서 분모에서 나누어 처리하기 위해 \( \,\, x^2 = x^2 +1 -1 \,\,\, \) 의 변형을 시도했다. 이 아이디어를 \( I'(a) \) 에도 바로 적용해보자.

\begin{equation*}
\begin{split}
I'(a) &= -\int_{0}^{\infty}\frac{x\sin ax}{1+x^2}dx\\[1.5ex]
&= -\int_{0}^{\infty} \frac{(x^2 +1 -1) \sin ax}{x(1+x^2)}\\[1.5ex]
&= -\int_{0}^{\infty} \frac{\sin ax}{x}-\frac{\sin ax}{x(1+x^2)}dx\\[1.5ex]
&= -\int_{0}^{\infty} \frac{\sin ax}{x} dx + \int_{0}^{\infty} \frac{\sin ax}{x(1+x^2)}dx\\[1.5ex]
\end{split}
\end{equation*}

ㅤ

이 때 \( a > 0\) 일 때, 사실 음수여도 별다른 차이가 없긴 하지만,

\[ \int_{0}^{\infty} \frac{\sin ax}{x} dx = \int_{0}^{\infty} \frac{\sin ax}{ax} a\, dx = \int_{0}^{\infty} \frac{\sin ax}{ax} d(ax) = \int_{0}^{\infty} \frac{\sin x}{x} dx = \frac{\pi}{2}\]

의 결과는 알고 있다고 가정한다.

\( J = \displaystyle \int_{0}^{\infty} \frac{\sin x}{x} dx \) 도 \( J (\alpha) = \displaystyle \int_{0}^{\infty} \frac{\sin x}{x} e^{-\alpha x} dx \) 로 적분이 수렴하도록 잡아주면 쉽게 풀린다.

ㅤ

\[ I'(a) = -\frac{\pi}{2} + \int_{0}^{\infty} \frac{\sin ax}{x(1+x^2)}dx \]

에서 한 번 더 미분하면 좋은 형태가 나온다. 즉 기쁘다.

\begin{equation*}
\begin{split}
I''(a) &=\frac{d}{da} \int_{0}^{\infty} \frac{\sin ax}{x(1+x^2)}dx\\[1.5ex]
&= \int_{0}^{\infty} \frac{\cos ax}{(1+x^2)}dx\\[1.5ex]
&= I(a)
\end{split}
\end{equation*}

ㅤ

미분 방정식이 등장했으므로 초기값을 찾자면,

\( I(0) = \displaystyle \int_{0}^{\infty} \dfrac{1}{1+x^2}dx = \dfrac{\pi}{2} \) 이고 ㅤㅤ \( I'(0) = -\dfrac{\pi}{2} + \displaystyle \int_{0}^{\infty} \frac{\sin 0 x}{x(1+x^2)}dx = -\frac{\pi}{2}\) 이다.

ㅤ

곧 문제를 풀기 위해 이차선형미분방정식,

\[ I''(a)=I(a) \,\,\, , \,\,\, I(0) = \frac{\pi}{2} \, , \,I'(0) = -\frac{\pi}{2} \]

을 풀어야 한다. 선형미분방적식을 푸는 방법은 글을 여기까지 읽은 사람이라면 알고 있겠으나 조금의 설명을 포함하겠다.

ㅤ

\[ I''(a)+I'(a)=I(a)+I'(a) \]

로부터 상수 \( c_1 \) 에 대하여

\[ I(a)+I'(a) = c_1 e^a \]

의 일차미분방적식을 얻는다. 그리고 \( a=0 \) 을 대입하면

\[ \frac{\pi}{2} - \frac{\pi}{2} = c_1 e^0 = c_1 \]

이므로 \( c_1 = 0 \) 를 얻는다.

\[ I'(a) = - I(a) + 0\]

로부터 상수 \( c_2 \) 에 대하여

\[ I(a) = c_2 e^{-a} \]

또 초기값 \(I(0)=\dfrac{\pi}{2}\) 에 의해

\[ I(a) = \frac{\pi}{2} e^{-a} \]

ㅤ

ㅤ

이로서

\[ I(k) = \int_{0}^{\infty} \frac {\cos kx}{1+x^2} dx = \frac{\pi}{2} e^{-k} \]

를 얻었다.

ㅤ

그럼 재미있는 결과로 \( k=1 \)을 대입하고 우함수의 성질을 이용하면

\[ \int_{-\infty}^{+\infty} \frac {\cos x}{1+x^2} dx = \frac{\pi}{e} \]

를 얻을 수도 있다.

ㅤ

마지막으로 \( I \) 에 이 결과를 대압해 마무리하자면

\begin{equation*}
\begin{split}
I &= \sum_{k=0}^{\infty} \frac{1}{k!} \int_{0}^{\infty} \frac {\cos kx}{1+x^2} dx\\[1.5ex]
&= \frac{\pi}{2} \sum_{k=0}^{\infty} \frac{e^{-k}}{k!} \\[1.5ex]
&= \frac{\pi}{2} \sum_{k=0}^{\infty} \frac{(e^{-1})^k}{k!} \\[1.5ex]
&= \frac{\pi}{2} e^{e^{-1}}
\end{split}
\end{equation*}

ㅤ

ㅤ

ㅤ

곧

\[ I = \int_{0}^{\infty} \frac{e^{\cos x} \cos(\sin x)}{x^2 +1} dx = \frac{\pi}{2} e^{\frac{1}{e}} \]

ㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

ㅤㅤ

ㅤ

더 메뉴, 곧 간다.