시리즈 | Integration - 오늘의 적분 4
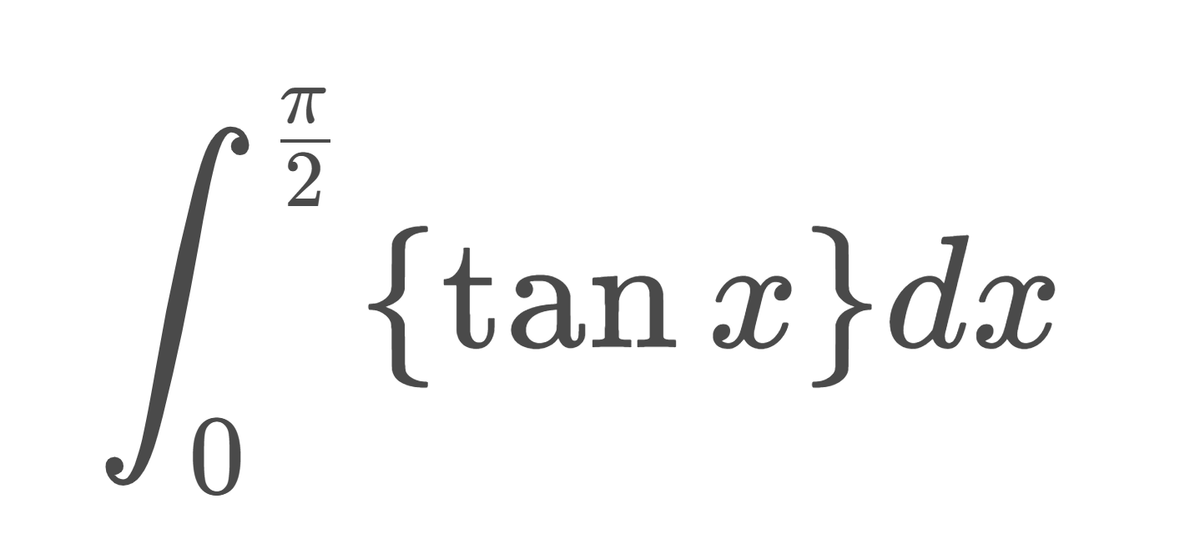
간결할수록 어려울 수 있다.
ㅤ
\[ \int_{0}^{\frac{\pi}{2}} \{ \tan x \} dx\]
ㅤ
ㅤ
ㅤ
ㅤ
여기서 \(\{ \}\)란 어떤 실수의 소수부분을 의미하며 엄밀히 쓰자면 다음을 만족하는 어떤 정수 \(n\)이 존재하여
\[ n \leq x < n+1 \,\,\, \Leftrightarrow \,\,\, \{ x\} = x-n \]
라 쓸 수 있다.
ㅤ
그러니 일단
\[ \text{let} \,\,\, I_n = \left\{ x \vert n\leq \tan x < n+1 \,\, , \, x \in \left[0, \, \frac{\pi}{2} \right) \right\} \]
이라 하면
\[ I_n = [ \tan^{-1} n , \, \tan^{-1} (n+1) ) \]
이므로 \( n \) 전부 동원하면 적분 구간을 빈틈 없이 채울 수 있다.
ㅤ
\[ I = \sum_{n=0}^{\infty} \int_{I_n} \tan x - n \, dx = \sum_{n=0}^{\infty} \int_{\tan^{-1} n }^{\tan^{-1} (n+1)} \tan x - n \, dx \]
\[ J_n = \int_{\tan^{-1} n }^{\tan^{-1} (n+1)} \tan x - n \, dx \]
라 두고 나서 계산한다. 이때 \( J_n \) 의 합을 구해야 하기 때문에 망원급수 형태로 변형하는 것을 목표로 한다.
\begin{equation*}
\begin{split}
J_n &= \int_{\tan^{-1} n }^{\tan^{-1} (n+1)} \tan x - n \, dx = [\, \ln (\sec x ) - n x \, \vert_{\tan^{-1} n}^{\tan^{-1} (n+1)} \\[2ex]
&= (\ln \sec \tan^{-1} (n+1) - n \tan^{-1} (n+1) ) - ( \ln \sec \tan^{-1} n - n \tan^{-1} n ) \\[2ex]
&= (\ln \sec \tan^{-1} (n+1) - \ln \sec \tan^{-1} n ) \\[2ex] & \,\,\,\,\,\,\,\,\, - ( (n+1) \tan^{-1} (n+1) - n \tan^{-1} n) + \tan^{-1} (n+1) \\[2ex]
\end{split}
\end{equation*}
ㅤ
그러나 이들의 합을 구한 각 항, \( \ln \sec \tan^{-1} n \), \( \,\,\, n \tan^{-1} n \), \(\,\,\, \displaystyle \sum_{k=1}^{n} \tan^{-1} k \) 는 수렴하지 않으므로 이들을 분리하여 극한을 계산할 수 없다. 그러니 이들을 모두 묶어 한 번에 처리해야 한다.
일단 큰 자연수에 대해 합을 나타내고
\[ \sum_{n=0}^{N} J_n = \ln \sec \tan^{-1} (N+1) - (N+1) \tan^{-1} (N+1) + \sum_{k=1}^{N+1} \tan^{-1} k \]
의 극한인 \( \displaystyle \lim_{N \to \infty} \) 의 경우가 \( I\) 의 값인 것이다.
ㅤ
먼저 지금 당장 볼 때 가장 성가시다고 할 수 있는 3개의 초월함수가 합성된 항을 정리하자면
\[ \sec^2 x = \tan^2 x + 1 \]
을 이용해 \( \tan^{-1} x \in \left( - \frac{\pi}{2} , \, + \frac{\pi}{2} \right) \) 의 범위 조건에 의해
\[ \ln \sec \tan^{-1} (N+1) = \frac{1}{2} \ln (1 + (N+1)^2 )\]
으로 변형한다.
ㅤ
그다음 \( (N+1) \tan^{-1} (N+1) \,\, , \,\,\, \displaystyle \sum_{k=1}^{N+1} \tan^{-1} k \) 에서는 역탄젠트의 각 변수가 무한대이기 때문에 이를 0으로 바꿀 수 있는 무언가가 팔요하다 느낀다.
\[ x \geq 0 \,\,\, \Rightarrow \,\,\, \tan^{-1} x = \frac{\pi}{2} - \tan^{-1} \frac{1}{x} \]
이므로 이들을 이용하면
\[ (N+1) \tan^{-1} (N+1) = (N+1)\frac{\pi}{2} - (N+1) \tan^{-1} \frac{1}{N+1} \]
\[ \,\,\, \sum_{k=1}^{N+1} \tan^{-1} k = (N+1)\frac{\pi}{2} - \sum_{k=1}^{N+1} \tan^{-1} \frac{1}{k} \]
곧 이 때 무한대로 발산하는 항 두개가 소거된다.
ㅤ
한 번 정리해 보면
\begin{equation*}
\begin{split}
I &= \lim_{n \to \infty} \left( \frac{1}{2} \ln (1 + (n+1)^2 ) + (n+1) \tan^{-1} \frac{1}{n+1} - \sum_{k=1}^{n+1} \tan^{-1} \frac{1}{k} \right) \\[2ex]
&= \lim_{n \to \infty} \left( \frac{1}{2} \ln (1 + n^2 ) + n \tan^{-1} \frac{1}{n} - \sum_{k=1}^{n} \tan^{-1} \frac{1}{k} \right)
\end{split}
\end{equation*}
그런데 여기서 중간의 항은 자명하게
\[ \lim_{n \to \infty} n \tan^{-1} \frac{1}{n} \, = \, \lim_{x \to 0^+} \frac{\tan^{-1} x}{x} \, = \, \lim_{t \to 0^+} \frac{t}{\tan t} = 1\]
이므로 따로 생각한다.
그리고 \(\displaystyle \lim_{n \to \infty} \frac{\sqrt{1 + n^2 }}{n} = 1 \) 에서 \( \displaystyle \lim_{n \to \infty} \frac{1}{2} \ln (1 + n^2 ) - \ln n =0\) 이므로 이 둘을 같은 것으로 생각할 수 있다.
ㅤ
ㅤ
결국
\[ I = 1+ \lim_{n \to \infty} \left( \ln n - \sum_{k=1}^{n} \tan^{-1} \frac{1}{k} \right) \]
ㅤ
극한에서 \( \ln \) 이 등장한다면 \( \displaystyle \sum \frac{1}{k} \) 을 살펴보는 것이 좋을 것이다.
오일러 마스케로니 상수,
\[ \gamma = \lim_{n \to \infty} \left( \left( \sum_{k=1}^{n} \frac{1}{k} \right) - \ln n \right) \]
를 활용할 수 있기 때문이다. 게다가 구해야하는 극한의 경우에 \( \displaystyle \sum_{k=1}^{n} \tan^{-1} \frac{1}{k} \) 에서 \( \displaystyle \sum_{k=1}^{n} \frac{1}{k} \) 을 뺀다면 역 탄젠트의 테일러 전개와 소거되기 때문이다.
\begin{equation*}
\begin{split}
I &= 1+ \lim_{n \to \infty} \left( \ln n - \left( \sum_{k=1}^{n} \frac{1}{k} \right) - \sum_{k=1}^{n} \tan^{-1} \frac{1}{k} + \left( \sum_{k=1}^{n} \frac{1}{k} \right) \right) \\[2ex]
&= 1 + \lim_{n \to \infty} \left( \left( \ln n - \sum_{k=1}^{n} \frac{1}{k} \right) - \left( \sum_{k=1}^{n} \tan^{-1} \frac{1}{k} - \frac{1}{k} \right) \right) \\[2ex]
&= 1 - \gamma - \lim_{n \to \infty} \left( \sum_{k=1}^{n} \tan^{-1} \frac{1}{k} - \frac{1}{k} \right) \\[2ex]
&= 1 - \gamma - \sum_{k=1}^{\infty} \left( \tan^{-1} \frac{1}{k} - \frac{1}{k} \right)
\end{split}
\end{equation*}
ㅤ
ㅤ
그러면
\[ S = \sum_{k=1}^{\infty} \left( \tan^{-1} \frac{1}{k} - \frac{1}{k} \right) \]
라 두자.
ㅤ
\( \tan^{-1} \) 의 테일러 전개라 하면 \( \mathbb{R^1} \) 의 열린 단위구에서 적용되는
\[ \sum_{n=0}^{\infty} x^n = \frac{1}{1-x} \]
에서 \( x \to -x^2 \) 로의 대입 후 적분한
\[ \sum_{n=0}^{\infty} (-1)^n x^{2n} = \frac{1}{1+x^2} \]
\[ \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{2n+1} = \tan^{-1} x \]
를 말하는 것이다.
ㅤ
\[ S = \sum_{k=1}^{\infty} \left( \tan^{-1} \frac{1}{k} - \frac{1}{k} \right) = \sum_{k=1}^{\infty} \left( \left( \sum_{n=0}^{\infty} \frac{(-1)^n }{(2n+1) k^{2n+1}} \right) - \frac{1}{k} \right) \]
에서 \( n=0 \) 인 경우 뒷부분 \( \displaystyle \frac{1}{k} \) 와 소거된다.
\[ S = \sum_{k=1}^{\infty} \sum_{n=1}^{\infty} \frac{(-1)^n }{(2n+1) k^{2n+1}} \]
이는 \( (k, \, n ) \in \mathbb{N}^2 \) 에 대한 \( \displaystyle \frac{(-1)^n }{(2n+1) k^{2n+1}} \) 값들의 합이므로 \( \sum \) 의 순서는 상관없다.
\begin{equation*}
\begin{split}
S &= \sum_{n=1}^{\infty} \sum_{k=1}^{\infty} \frac{(-1)^n }{(2n+1) k^{2n+1}} \\[2ex]
&= \sum_{n=1}^{\infty} \left( \frac{(-1)^n}{2n+1} \sum_{k \in \mathbb{N}} \frac{1}{k^{2n+1}} \right) \\[2ex]
&= \sum_{n=1}^{\infty} \frac{(-1)^n \zeta (2n+1)}{2n+1}
\end{split}
\end{equation*}
ㅤ
ㅤ
이 때
\[ \sum_{n=1}^{\infty} \frac{ \zeta (2n+1)}{2n+1} x^{2n+1} = - \gamma x + \frac{1}{2} \operatorname{Ln} \left( \frac{\Gamma (1-x)}{\Gamma (1+x)} \right) \]
임이 밝혀져있다.
사실 밝혀져 있다는 말을 하기 민망하게 이질적이고 비직관적인 결과이다.
https://youtu.be/Vlycysh4OlI?si=yFYmGIOYQFq6Rhxg
기본적으로 감마함수의 바이어슈트라스 무한곱 꼴로부터 유도된다.
\[ \frac{1}{\Gamma (1+z)} = e^{\gamma z} \prod_{n=1}^{\infty} \left( 1 + \frac{z}{n} \right) e^{- z/n} \]
말이다.
ㅤ
감마함수는 로지케이에서 자주 얼굴을 비춘 특수 함수로
\[ \Gamma (z) = \int_{0}^{\infty} t^{z-1} e^{-t} dt \,\,\,\,\,\,\,\,\, ( \mathrm{Re} (z) > 0 ) \]
으로 정의한다. 그러나 본 글에서 중요한 것은
\[ \Gamma ( \overline{z} ) = \overline{\Gamma (z)} \]
가 성립한다는 사실이다.
ㅤ
일단 위의 식에서 \( (-1)^n \) 을 이끌어내기 위해 \( x = i \) 를 대입한다.
\[ \sum_{n=1}^{\infty} \frac{ \zeta (2n+1)}{2n+1} i^{2n+1} = - \gamma i + \frac{1}{2} \operatorname{Ln} \left( \frac{\Gamma (1-i)}{\Gamma (1+i)} \right) \]
\[ \sum_{n=1}^{\infty} \frac{ (-1)^{n} \zeta (2n+1)}{2n+1} = - \gamma + \frac{1}{2i} \operatorname{Ln} \left( \frac{\Gamma (1-i)}{\Gamma (1+i)} \right) \]
ㅤ
따라서 이를 그대로 대입하면 답이 나온다. 그러나 이 전에 위 \( \displaystyle \operatorname{Ln} \left( \frac{\Gamma (1-i)}{\Gamma (1+i)} \right) \) 를 간단히하는 과정을 거친다.
\begin{equation*}
\begin{split}
\operatorname{Ln} \left( \frac{\Gamma (1-i)}{\Gamma (1+i)} \right) &=
\operatorname{Ln} \left( \frac{\Gamma (1-i)}{\Gamma (\overline{1-i})} \right) \\[2ex]
&= \operatorname{Ln} \left( \frac{\Gamma (1-i)}{\overline{\Gamma (1-i)}}
\right) \\[2ex]
&= 2i \operatorname{Arg} \Gamma (1-i) \\[2ex]
&= - 2i \operatorname{Arg} \Gamma (1+i)
\end{split}
\end{equation*}
\( \bar{z} \)는 크기가 \( z \) 와 같고 \( \operatorname{Arg} \) 의 값은 마이너스 관계에 있으므로 \( \operatorname{Ln} \) 의 정의로 유도할 수 있다.
ㅤ
ㅤ
따라서
\[ S = -\gamma - \operatorname{Arg} \Gamma (1+i) \]
이다.
이를 대입하면
\[ I = 1 - \gamma - S \]
ㅤ
ㅤ
\[ \int_{0}^{\frac{\pi}{2}} \{ \tan x \} dx = 1 + \operatorname{Arg} \Gamma (1+i) \]




Comments ()